基于二进制搜索的RFID 标签防碰撞算法研究
蒋 霞 白铁成 郑洪江
(塔里木大学信息工程学院,新疆 阿拉尔 843300)
射频识别RFID(Radio Frequency Identification)是一种自动识别技术[1]。它以射频方式进行非接触式双向通信,以达到自动识别目标并获取其相关数据的目的。但目前RFID 技术也存在着很多亟待解决问题,例如安全和隐私,数据存储和碰撞等。标签防碰撞算法是RFID 系统需要研究和解决的一个重要课题。目前存在的RFID 防碰撞算法主要有2种:一种是基于ALOHA的不确定性算法[2],另一种是基于二进制问询的确定性算法。本文就基于二进制的RFID 标签防碰撞算法进行了研究和改进。
1 二进制搜索的防碰撞算法介绍
二进制搜索算法的基本思想是将处于碰撞的标签根据碰撞位分成左右两个子集,先查询一个子集,若没有碰撞,则正确识别,若仍有碰撞则再分裂,依次类推,直到识别出子集中的所有标签,再查询另一个子集[3]。为了最简捷地找到碰撞位,数据编码选用曼彻斯特编码[4]。依据曼彻斯特编码的特点可以检测出碰撞位。
为了实现算法,需要引入一组阅读器命令[5],这组指令能被标签处理。以下为了举例,假定标签唯一的序列号ID 长度为8 bit,也就是说最多可以有256 个标签处于运行状态,实际中ID 较长。
REQUEST:请求命令,其参数根据算法而不同,该命令给向阅读器识别范围域内的所有标签发送参数,标签收到该命令后把自己的ID 与接收的相比较,若小于或者等于,则此标签用其序列号回应阅读器。若大于则不作任何回应。
SELECT:选择命令,阅读器用序列号作为参数发送给标签,具有相同的序列号的标签将以此作为执行其命令(读出和写入)切入开关,即选择了这个标签[6]。
RD-DATA:读出选中的标签,使其将存储的数据发送给阅读器。
UNSELECT:去选择,取消一个被选中操作完的标签,让其进入“无声”状态,这样标签对收到的REQUEST 命令不再作回复。为了重新激活此类标签,必须进行复位操作。
1.1 二进制树搜索(BS)算法
1.1.1 算法描述
在BS 算法中,REQUEST 命令的参数为标签的序列号ID。以4 个在阅读器范围内的标签为例,说明这种算法的原理和标签识别过程。标签ID 分别为:10110010、10100011、10110011、11100011。
第一步,阅读器向识别分为内所有合法标签发送REQUEST(11111111)命令,所有标签都用其序列号ID 响应,用曼彻斯特编码得到解码数据为1X1X001X,X 位碰撞位,得到下一次请求命令所需的参数。
第二步,阅读器发送REQUEST(10111111),标签1、标签2 和标签3 响应。阅读器得到解码数据为101X001X。
第三步,阅读器发送REQUEST(10101111),只有标签10100011 响应,无碰撞发生,阅读器对该标签进行处理后对它进行屏蔽操作,使其进入“无声”状态。重复上述过程直到识别完所有的标签。
标签2 通过3 次请求被阅读器识别,应答RDDATA 命令。在读出活写入操作完成之后,阅读器用UNSELECT 命令让其进入“无声”状态,这样标签2 对后面的请求命令不再作应答。阅读器用标签1经过3 次请求被阅读器识别到,标签3 经过1 次请求命令被识别,最后标签4 被识别。
1.1.2 性能分析
从大量的标签中识别出一个标签,需要多次问询操作。其平均问询次数由阅读器识别范围内的标签总数n 决定,如公式(1)所示[7]。

BS 算法可以快速简单地解决标签碰撞问题。如果在阅读器识别范围内只有一个标签,那么只需要一次问询操作即可识别标签,没有碰撞发生。如果在阅读器的识别范围内有多于一个的标签,那么问询次数的平均值很快增加。
在8 位ID的标签识别过程中,通过3 次问询过程,另外加上最开始的1 次共操作[7],完成一个标签的识别平均需要4 次操作。在n 个待识别标签中,完成n 个标签的识别需要的总问询次数如公式(2)所示。

所有标签都需要发送完整的ID 来响应阅读器的每一次查询。识别n 个k 位序列号标签,阅读器需要传输的总比特数为标签序列号长度与算法总问询次数的乘积,如公式(3)。
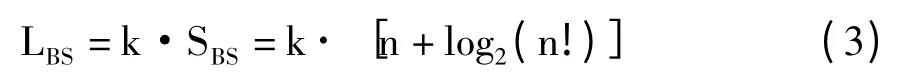
1.2 动态二进制搜索(DBS)算法
1.2.1 算法思想
上述BS 算法,不仅搜索的范围较大,而且标签的序列号ID 每次完整地传输。而在实际中标签的序列号长度按系统的规模可能长达96bit 或更长,为了选择一个标签,数据传输量较大。因而DBS 算法被提出。
DBS 算法是国际标准ISO14443A 所推荐的防碰撞算法[8]。在BS 算法中,阅读器传输的请求命令序列号与标签应答的序列号部分信息是重复的,可以不必传输,这样就得到了DBS 算法,如图1 所示。DBS 算法中,假定K 为标签序列号的最高位,请求命令为REQUEST(ID(K~X),X),X 为碰撞的最高位,序列号的K~X 位与参数相符的标签,传输其(X-1)~0 位作为对阅读器的响应。

图1 DBS 算法原理
下 面 以 4 个 标 签(10110010、10100011、10110011、11100011)为例说明标签算法的执行过程。
第一步,阅读器发送REQUEST(NUL),处于阅读器识别范围的所有标签都用其序列号响应,通过曼彻斯特编码得到解码数据为1X1X001X,碰撞最高位是第6 位,将该位置“0”,高于该位的不变,可得到下一次请求命令所需的参数(10)。
第二步,阅读器发送REQUEST(10),序列号前缀为10的标签响应,即标签10110010、10100011 和10110011 响应。返回各自的后6 位信息110010、100011、110011。阅读器得到解码数据为1X001X,将碰撞最高位D4 置为“0”,得到下一次命令所需的参数(1010)。
第三步,阅读器发送REQUEST(1010),只有序列号前缀为1010的标签2 响应,阅读器处理完标签2 后用UNSELECT 命令使其进入“无声”状态。然后不断重复上述操作直到所有标签识别完。
1.2.2 算法性能分析由于DBS 算法与前面的基本二进制算法使用相似的搜索过程,因此在限制查询范围时动态二进制搜索算法也可以釆用与基本二进制算法相同的重复操作。故而可以得出动态二进制搜索算法总搜索次数如公式(4)。

DBS 算法识别标签时,首先要求作用范围内的所有标签都上传各自的序列号,n 个标签的序列号总长度就是第一次上传的数据长度,即整个序列号长度作为传输比特数。对某个标签进行识别时,可以设标签动态传输序列号部分位的平均值等于BS算法一半[7]。标签需要传输的比特数为公式(5)所示。

将公式(3)和公式(5)比较,可以看出,采用DBS 算法时,标签传输的数据量和传输时间比BS算法减少了近50%。阅读器识别一次传输平均数据量为[9]公式(6)所示。

当阅读器使用动态二进制搜索算法时,识别n个标签所需要传输的序列号总长度为公式(7)所示。
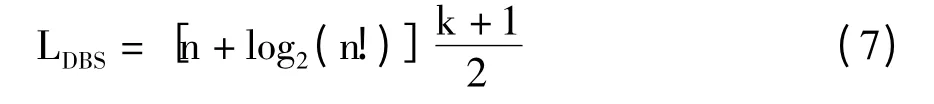
下图为BS 与DBS 算法中阅读器用于问询标签传输序列号总长度比较。可以看出随着标签数的增多,DBS 算法所需的数据量是BS 算法的一半,提高了效率。
1.3 返回式二进制搜索(BBS)算法
1.3.1 算法的基本思想
BS 算法与DBS 算法之所以效率较低.最根本原因在于其无记忆性[10]。其识别完一个标签,都要从头再来,把剩下的标签全部问询一遍,而没有利用上次搜索已经获得的信息来缩小搜索范围。
返回式策略是阅读器每完成一个标签的读取,不是返回到根节点而是返回上一个碰撞发生的节点,识别此节点的另外一个分枝,这样不断重复操作,直到把所有标签识别完[11]。
1.3.2 性能分析
BBS 算法在识别n 个标签时,阅读器共需搜索2n-1 次,当标签数增多时,平均搜索次数为2 次。假设标签序列号长度为k bit,则阅读器发送的数据量为k(2n-1)bit。通过画图比较BS、DBS 和BBS之间的优劣。假设k=96。
从图2 可以看出,基于BBS的算法相比DBS 算法有了改进,问询数据量减少了25%,较BS 算法减少了57%。DBS的优点是减少了REQUEST 命令的参数长度,而BBS的优点是减少了问询次数,如果能将两者的优势结合,必能提高性能。基于此本文提出了以下改进算法。
2 改进的二进制防碰撞算法
2.1 返回式动态二进制算法BDBS
根据以上三种基于二进制防碰撞算法的分析,本文研究了结合DBS 和BBS的优点的返回式动态二进制算法。由于该算法基于返回式算法和动态算法,因此简称为BDBS。其请求命令为REQUEST(ID(K~X),X),序列号K~X 位与之一致的标签传输剩余的(X-1)~0 位信息作为应答,阅读器完成一个标签的识别后,返回上一个碰撞发生节点,识别该节点的另外一个分枝,而不是返回根节点,不断重复操作,直到把每一个节点碰撞的所有标签识别完。
在BDBS 算法中,阅读器的问询次数为2n-1,阅读器每次问询平均传输的数据量为(k +1)/2,所以阅读器识别所有标签所需要发送的数据量为公式(8)所示。

根据以上的对比分析,可以得出如图2 所示仿真图。
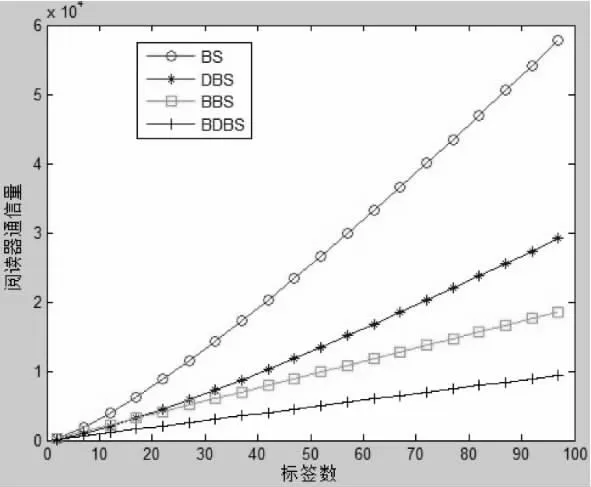
图2 几种算法搜索数据量比较
从仿真图2 可以较为明显地得出结论,对于返回式动态二进制搜索算法,阅读器用于识别标签的数据通信量最少,比返回式二进制搜索算法通信量减少近50%,比动态二进制搜索算法减少约67%,比BS 算法减少了约83%。
2.2 改进的BDBS 算法IBDBS(Improved BDBS)
在识别中,若遍历到碰撞位只有一位时,说明只有两个标签发生碰撞,则认为没有发生碰撞。对一个标签的碰撞位认为是“0”。另一个标签的碰撞位认为是“1”,直接使用SELECT(ID)命令选择标签。则阅读器的问询次数减少为公式(9)([]为向上取整)。

则完成n 个标签识别,阅读器的数据通信量为公式(10)所示。
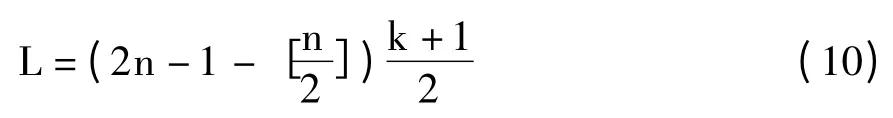
对阅读器的问询通信数据量进行比较。如图3所示,IBDBS 标签问询数据量较BDBS 减少了约25%,性能得到了提高。
说明:此处如果考虑标签搜索树为满树,问询次数应减掉n,如果搜索树为非满树,减去n 显然太多,最差的情况是减去2,取中间值n/2,这种取值使得仿真与实际性能之间有一定差距,但总体是有了改进。
下面从系统吞吐率性能来分析几种算法,假设系统标签数量为n,问询标签的平均操作数为L(n),则定义系统吞吐率为公式(11)。

则BS、BDBS 及IBDBS 算法下系统的吞吐率分别为公式(12)、(13)、(14)。
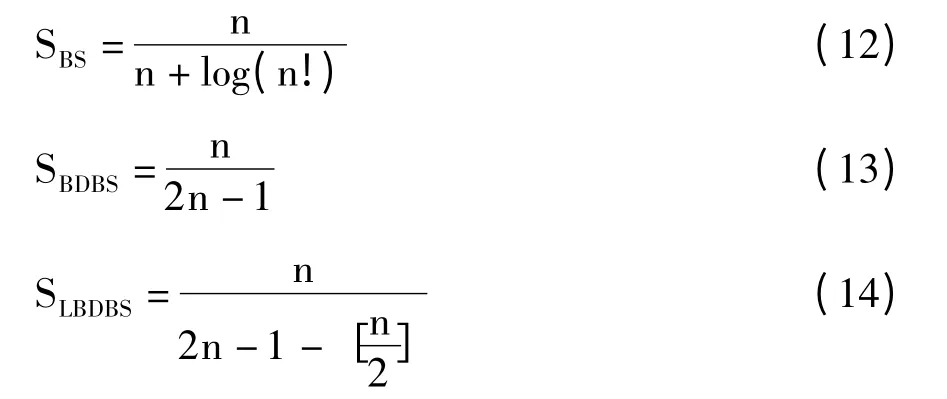
对几种算法吞吐率进行仿真比较如图4 所示。随着标签数量的增多,BS 算法的吞吐率随标签数量的增多不断减小,BDBS 算法的吞吐率稳定在50%,IBDBS 算法的吞吐率趋近于67%,相比较有了较大的提升。但是在IBDBS 中,请求命令REQUEST的参数长度当碰撞最高位较低时依然较长。而在REQUEST 命令中实际需要的只是最高碰撞位的位置,因此只要得到碰撞最高位的位置就可以了。

图3 BDBS 与IBDBS的问询数据量比较

图4 三种算法吞吐率比较
李学桥等人在文献[12]中提出了一种新的标签搜索算法,在REQUEST(x)命令中,x 为碰撞最高位,即请求命令只传输碰撞最高位的二进制表示,请求第x 位为0的标签响应。这种算法中搜索的数据长度为log2(k),比如ID 为96 位的标签,x的长度为log296,即x 可用7 位二进制表示,比DBS 算法请求命令(k +1)/2 减少了42 位,极大地减少了问询标签的数据通信量,节省了信道资源,提高标签识别的速度。将这种算法与IBDBS 算法问询次数少的优势相结合,其吞吐率没有改善,但是标签问询数据量大大减少,如公式(15),当标签数量接近100 时,比IBDBS 问询数据量减少了约86.5%。如图5所示。
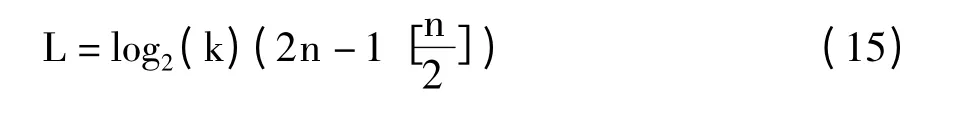

图5 IBDBS 与新改进算法的问询数据量比较
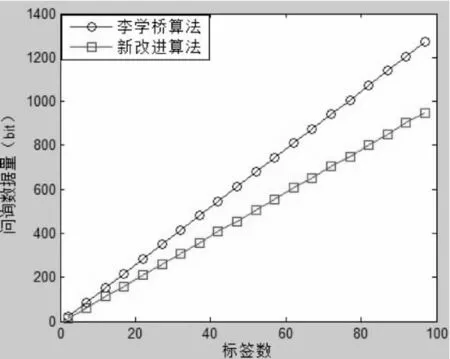
图6 新改进算法与李学桥算法比较
在李学桥的改进算法中,标签问询次数为2n-1 次,比本文的改进算法多,比较两种算法的问询数据量如图6 所示,仿真图中新算法比李学桥改进算法有所提高,当标签数量增多时,问询数据量减少25%。
3 结论
本文分析了结合DBS 及BBS 优点的返回式动态二进制算法BDBS,对三者的在标签问询通信数据量及吞吐率等性能方面进行了仿真比较,提出了改进的BDBS 算法IBDBS,将只有一位碰撞的情况认为无碰撞进行识别,系统性能得到较大的提高。基于李学桥等人提出的对REQUSET 命令参数的改进,本文对IBDBS 算法进行了新的改进,传输数据量进一步减少,系统吞吐率得到了提高,算法性能有了改进。仿真结果表明,通过对算法的改进,能有效地提高标签识别的速度。
[1]史军晖.基于捕获效应的RFID 防碰撞算法研究[D].广东工业大学.2012.
[2]王雪,钱志鸿,胡正超.基于二叉树的RFID 防碰撞算法的研究[J].通信学报.2010,31(6):49-56.
[3]王秀玲,耿淑琴,蒙荣生,等.二进制搜索算法在系统中的实现.中国通信学会第五届学术年会论文集[C].2008.
[4]周晓光,王晓华.射频识别(RFID)技术原理与应用实例[M].北京:人民邮电出版社.2006:25-30.
[5]李兴鹤,胡咏梅.基于动态二进制的二叉树RFID 搜索结构反碰撞算法[J].山东科学.2006(2):51-55 .
[6]江岸.无线射频识别系统中防碰撞问题的研究(D).湖南大学.2009.
[7]杨恒.射频识别-RFID 防碰撞算法研究(D).西南石油大学.2012.
[8]ISO/IEC 14443-3 identification cards contactless integrated circuit (s)card-proximity cards,part 3.initialization and anti-collision[S].2003.
[9]鞠伟成,俞承芳.一种基于动态二进制的RFID 抗冲突算法[J].复旦学报自然科学版.2005(01):46-50.
[10]刘康.基于无源RFID 标签防碰撞算法的研究(D).山东大学.2012.
[11]余松森,詹宜巨,彭卫东,等.基于后退式索引的二进制树形搜索反碰撞算法及其实现[J].计算机工程与应用,2004,40(16):26-28.
[12]李学桥,贾小爱,赵磊.基于后退式索引的动态树形防碰撞算法[J].通信技术.2009,06(42).118-120.

