基于经验分布假设的风电功率预测误差分析

马淑清

(内蒙古大学交通学院，内蒙古呼和浩特 010020)

0 引言

风电功率预测是目前公认的解决风电接纳问题的有效手段，精确的预测有助于风电调度工作的顺利进行，提高风电接纳能力［1，2］。常用的风电功率预测以确定性的单值预测为主，如时间序列自回归滑动平均(ARMA)模型［3］、卡尔曼滤波［4］、支持向量机［5］、神经网络模型［6］等。

目前国内风电功率预测水平有限，以超短期预测为例，国家对4 h超短期预测精度要求为不低于85%［7］，这一标准基本可以体现国内目前的超短期功率预测水平，而短期预测平均绝对误差则保持在装机容量的25%～40%，不是十分理想。

由于预测精度不高，单值功率曲线形式的风电功率预测结果容易对风电调度工作产生误导作用，间接增加系统调度负担。为了应对这一问题，基于功率预测误差的风电功率不确定性预测近年来得到了更多的研究:

文献［8］～［10］在正态分布模型的基础上，利用概率密度函数、蒙特卡洛随机模拟、基于分位数的非参估计等理论，分析了风电功率预测误差的不确定性及对调度的影响，具有一定的积极性。

然而，上述研究成果对预测误差的描述没有脱离传统分布假设的束缚，适应的场景有限。

本文以风电功率预测误差为研究对象，通过引入预测误差经验分布假设，实现对风电功率预测误差分布的描述，并根据预测误差时间序列高阶AR模型对未来预测误差进行估计，为确定预测结果置信度与预测结果修正奠定了基础。由于研究对象为预测误差本身，该方法具有很高的适应性，适用于各算法下的风电预测系统，算例分析证明了所提方法的有效性。

1 预测误差的经验分布假设

以风电功率预测误差为对象，对其概率分布进行描述可以确定预测结果的置信度及置信区间。实际应用中常用经验分布假设对预测误差真实分布进行拟合。当样本容量足够大时，经验分布函数依概率收敛于总体分布函数。

1.1 预测误差的经验分布函数

设有预测误差样本值(x1，x2，…，xn)，作函数:

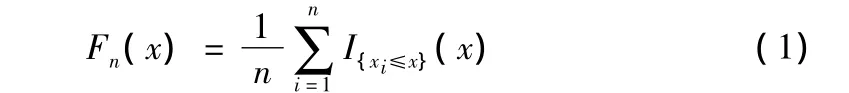
这里IA(·)表示集合A的示性函数，Fn(x)表示样本(x1，x2，…，xn)的经验分布函数。对任意实数x，Fn(x)表示样本x1，x2，…，xn落入区间(－∞，x］内的频数概率。由大数定律，对于提取出的每组样本值，当n→∞时，Fn(x)依概率收敛到Fn(x)=P{X≤x}。因此当n很大时，可以用Fn(x)作为对实际预测误差分布函数的估计。

1.2 风电功率预测误差经验分布的适用性

根据出力水平将历史数据分为高、中、低出力水平的样本集并构造经验分布函数，图1为中出力水平样本由统计频数表示的离散经验分布直方图。由经验分布图示可以看出风电功率预测误差并不完全是通常意义上的正态分布或者韦布尔分布，可拟合性差。

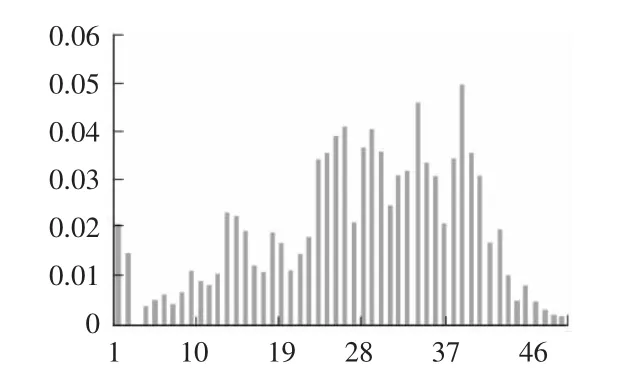
图1 中出力水平经验分布直方图

经验分布不作随机变量服从某种特定分布的假设，避免了拟合度的问题，能够对预测误差的分布进行更精确的描述，当样本数据量足够大时完全可以作为对实际分布的估计［11］，与传统特定分布相比，约束更小，适应性更强。

2 时间序列高阶AR误差预测模型

以风电功率预测误差本身作为预测对象，对未来可能出现的预测误差进行初步的预测并修正，能够提高风电概率预测的精度。本文选择时间序列高阶AR模型估计预测误差。

2.1 时间序列高阶AR模型

ARMA模型描述随机过程较为精确，且建模简易。其中，AR模型参数估计通常只需求解一组线性方程，并且只要选择足够高的阶数就能够达到要求的逼近精度［12］。本文采用高阶AR模型对风电功率预测误差进行预测。

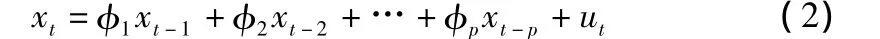
式中:φi——回归参数，i=1，…，p;

ut——白噪声过程。

高阶AR模型参数的具体求解过程见文献［13］，此处不再详细介绍。

2.2 高阶AR模型对预测误差随机过程的适用性

ARMA模型在风速预测、风电功率预测领域应用广泛，但是随着预测时间的增长，预测将转换为纯自回归形式。此时，高阶AR模型对ARMA模型的逼近精度足够高，用高阶AR模型取代ARMA模型进行预测是完全可行的。另外，高阶AR模型是线性模型，运算效率高，更具实时应用价值。因此本文选择高阶AR模型作为估计未来风电功率预测误差的核心算法。

3 基于经验分布假设的预测误差分析模型

根据上文中提及的经验分布假设与高阶AR模型可以对预测误差概率分布的特点进行初步的分析并得到置信区间结果，然而上述描述过程包含的信息过于笼统，无法有针对性的对不同条件下的风电功率预测误差分布进行详细讨论。

根据历史预测功率水平，将样本集分为高、中、低三个出力水平，并分别形成预测误差的经验分布函数，可以实现对预测误差分布的针对性估计。

整个预测误差不确定性分析流程如图2所示。

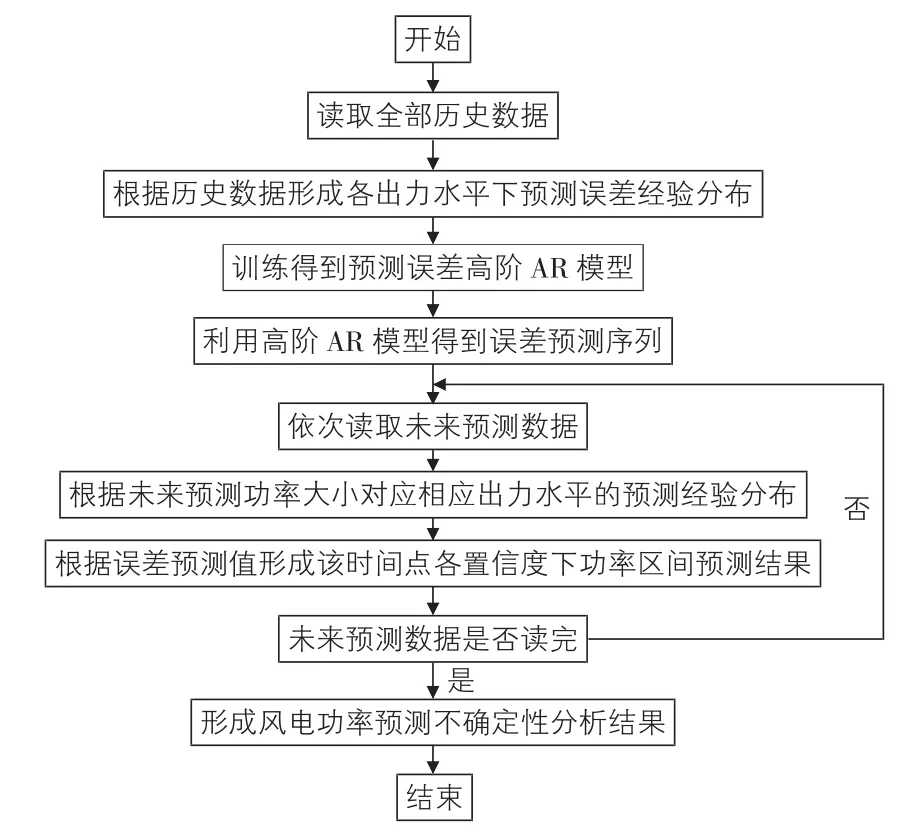
图2 程序流程图

4 实例分析

本文以内蒙古某风区2010年10月～2011年6月为样本对所提算法效果进行检验，筛选处理后的有效样本数为1 035。这里选取其中时长约为16 h的功率区间预测结果说明本文算法的有效性。

在高阶AR模型修正的基础上，根据预测误差经验分布函数展开预测误差不确定性分析工作。如图3，图4所示为90%与50%置信度下的功率区间预测结果。

图3 90%置信度功率区间结果

比较图3与图4可以发现，随着置信度的降低，功率区间上下界的间距逐渐减小，对测量数据的包络度逐渐降低。根据经验分布假设，当样本数量足够大时，功率区间对测量数据曲线的包络程度近似于置信度，即置信度为90%的功率区间理论上可以将测量数据曲线的90%包络。预测功率区间对测量数据曲线的包络程度越好说明越能对预测过程中的不确定性进行考虑。通过统计本文所提算法的功率区间包络情况，可以得到风电功率预测的不确定性分析结果，如表1所示。需要说明的是，由于经验分布样本和预测样本数有限，得到的实际包络度和理论置信度存在一定的偏差。

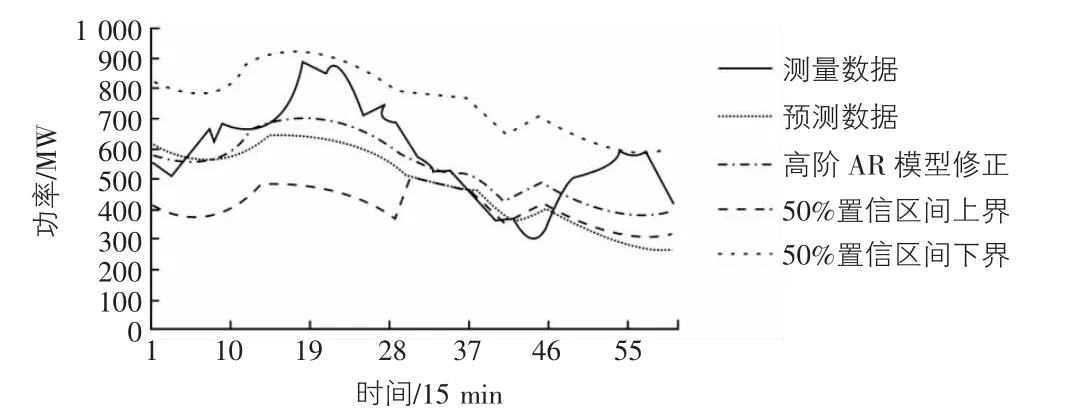
图4 50%置信度功率区间结果

表1 功率预测区间包络情况 %

5 结语

本文以风电功率预测误差为研究对象，通过引入预测误差经验分布假设，实现对风电功率预测误差分布的描述，并根据预测误差时间序列高阶AR模型对未来预测误差进行估计，为确定预测结果置信度与预测结果修正奠定了基础。实际调度运行中，根据风电出力置信度的要求，计算得到区间形式的预测结果，此区间信息可以为调度指令提供参考，具备良好的工程应用价值。

［1］谷兴凯，范高峰，王晓蓉，等.风电功率预测技术综述［J］.电网技术，2007，31(2):335-338.

［2］王丽婕，廖晓忠，高 阳，等.风电场发电功率的建模和预测研究综述［J］.电力系统保护与控制，2009，37(13):118-121.

［3］曾 鸣，李树雷，王 良，等.基于ARMA模型和BP神经网络组合优化算法的风电预测模型［J］.华东电力，2013，41(2):347-352.

［4］李 智，韩学山，韩 力，等.地区电网风电场功率超短期预测方法［J］.电力系统自动化，2011，45(5):47-51.

［5］杨 洪，古世甫，崔明东，等.基于遗传优化的最小二乘支持向量机风电场风速短期预测［J］.电力系统保护与控制，2011，39(11):44-48.

［6］范高锋，王伟胜，刘 纯，等.基于人工神经网络的风电功率短期预测系统［J］.电网技术，2008，32(22):72-76.

［7］Q/GDW 392-2009，国家电网公司企业标准［S］.

［8］刘 斌，周京阳，周海明，等.一种改进的风电功率预测误差分布模型［J］.华东电力，2012，40(2):286-291.

［9］刘永前，史 洁，杨勇平，等.基于预测误差分布特性的风电场短期功率预测不确定性研究［J］.太阳能学报，2012，33(12):2179-2184.

［10］Pierre Pinson，George Kariniotakis.Conditional Prediction Intervals of Wind Power Generation［J］.IEEE Trans On Power Systems，2009(8):29-30.

［11］张建华，曾建潮.经验分布函数概率模型的分布估计算法［J］.计算机工程与应用，2011，47(8):33-35.

［12］余辉里.ARMA谱的高阶AR估计方法［J］.电子科学学刊，1986，8(6):457-461.

［13］张晓峒.应用数量经济学［M］.北京:机械工业出版社，2009:266-273.