摇珠法在工程招投标过程中的报价分析
张 华
(中铁大桥局第九工程有限公司,广东中山 528400)
1 摇珠法的简述及评估方法
摇珠法是一种基于随机原理的招标方法,在我国建设工程招投标领域中发展较快,对小球进行编号并赋予每一编号以特定的含义,将带有号码的小球放在摇珠机内,摇珠机启动后,若干个带有号码的小球即在透明的圆形容器里翻滚,现场人员对抛出的号码进行监督和确认,这一过程叫做摇珠。用摇珠方式开展招投标活动的方法叫做摇珠法。摇珠法利用了摇珠过程的随机性,最大限度地避免了人为因素对招投标结果的影响,提高了招投标的公正性和公平性。
本文研究一种基于随机原理的综合评估法。它的分值(总分100分)由两个信封的分值构成(商务及技术文件的分值:20分;投标报价和工程量清单的分值:80分)。最终的中标候选人次序按两个信封的综合得分从高到低进行排名,如果综合得分相同,以投标报价较低的投标人排名优先。
第一个信封(商务及技术文件)的分值:共20分。
1)施工组织设计:10分;2)财务能力:2分;3)业绩:3分;4)履约信誉:5分。
其中,履约信誉得分分别由信用等级得分(5分)和履约情况(根据不同情况进行扣分)给出。信用评价级别由权威部门给出(我们这里研究的案例由广东省交通运输厅最新一年度的信用评价给出),其中:
1)信用评价为AA级单位信誉得分为5分;2)信用评价为A级单位信誉得分为4.2分;3)信用评价为B级单位信誉得分为3.6分;4)信用评价为C级单位信誉得分为3分。
第二个信封(投标报价和工程量清单)的分值:共80分。
首先,招标人提前公布投标人的控制价和下浮率范围;具体的下浮率开标前在开标现场采取摇珠方式确定。摇珠操作办法如下:在下浮率摇珠范围内,以0.1%为一档次增序确定摇珠号码(不放回地)摇取3个球,摇出3个球对应的下浮率的平均值即为本招标的下浮率。
招标人最高投标限价=招标人控制价×(1-下浮率)。
评标基准价=招标人最高投标限价×0.98。
投标人评标价的偏差率=100% ×(投标人评标价-评标基准价)/评标基准价。
投标人评标价得分=80-|投标人评标价的偏差率|×100×P,其中当投标人评标价大于评标基准价时,P=3;否则P=1(评标价得分精确到小数点后四位)。
根据综合评分法的分值分配原则,如果在所有投标人当中只有一个信用评价为AA级单位,那么这个单位就可以利用这0.8分的优势,并结合第二个信封的评分规则尽可能地最大化自身的中标成功率。同理,如果在所有投标人当中信用评价为AA级单位不只是一个,那么每个AA级单位的最大对手就是其他的AA级单位,它的策略是在没有第一个信封的优势的情形下,尽可能最大化自身的第二个信封的得分以最大化自身的中标成功率。而在有信用评价为AA级单位参加投标的情况下,信用评价为A级单位应该详细地分析AA级单位的最优报价策略,从而有针对性地进行报价投标,以最坏打算最好期望的报价方式进行投标报价,尽可能地抵消与AA单位的信誉得分差距,最终极大化自身中标的概率。
2 摇珠法确定的下浮率分析
在这里我们仅分析招标人给出的下浮率范围在2%内浮动的情形。假设招标人给出的下浮率范围为4.0%~6.0%,则在开标时取记有1~21数字的21个球,分别对应下浮率4.0%,4.1%,…,6.0%。然后不放回地取出3个球,其数字的平均值所对应的下浮率为此次投标的下浮率。容易想到的是,所抽取的三个球的代码和可以是6,7,8,…,60。从21个不同的球取出3个球总共有C(21,3)=1 330种不同取法。
然而,和为6的取法只有一种就是取出的3个球分别对应的数字(不计取出的顺序)是1,2,3,因为6=1+2+3。同理,和为7的取法也只有一种,因为7=1+2+4。但是和为8的取法有两种,即8=1+2+5=1+3+4。从而,相对于投标人取下浮率为4.1%(1+2+3的平均值2所对应的下浮率)并恰好投中该下浮率的概率,投标人取下浮率为4.166 7%(8=1+2+5=1+3+4的平均值2.667所对应的下浮率)并投中该下浮率的概率增加了一倍。特别地,和为32,33以及34的不同取法都是50种,这是在最大的取法数目。也就是说,如果把摇珠看成买彩票,只有买中确切的三数和的数目才能中奖的话,买32,33和34都是胜算最大的,中奖概率都达到50/1 330。而买6,7,59,60的中奖率最小,为1/1 330。
下面,我们用计算机程序计算出所有三数和出现的频率(如表1所示)。
下面考虑在所有投标人当中只有一个信用评价为AA级单位的情形。
2.1 AA单位的优势分析
该AA级单位可以利用这0.8分的优势,选出一个最佳的下浮率x,使得该单位的胜率最高。由于当投标人评标价小于评标基准价时,1%的偏差率对应于1分的扣分规则;而当投标人评标价大于评标基准价时,1%的偏差率对应于3分的扣分规则。从而AA级单位希望在这个规则下选取的x可以利用0.8分的优势覆盖尽可能多的下浮率。而0.8分的优势可以转换为32个下浮率覆盖面(根据规则,如果AA单位选取下浮率x,则它的覆盖区间为(x-0.8%,x+0.8%/3)。由于表1中每三个数对应0.1%的浮动率,比如三数和 6,7,8分别对应于下浮率 4.1%,4.133 3%,4.166 7%,从而区间(x-0.8%,x)可以覆盖8 ×3=24 个数,(x,x+0.8%/3)可以转换为3×8/3=8个数,合计为32个数。下面我们通过计算机程序运算给出所有连续的32个频率和最大值为1 180,对应的下浮率为5.266 67%。此时,该AA单位所选定的下浮率x对应的三数和分别为41和42,所覆盖的三数和分别从17~48和从18~49。此时,此AA单位的胜算可以达到1 180/1 330=0.887 2,即它的胜算可以达到 88.72%。

表1 三数和出现频率统计表
2.2 A级单位的对策
综上所述,如果有AA级单位(不管是有一家还是一家以上),则一般情况下A级单位与它的差距在0.8分。当AA级单位选择下浮率为5.266 67%时,则A级单位的胜算只能博剩下未被AA级单位覆盖的下浮率,对应于三数和为6~16以及50~60。由于6~16和50~60分属上下半区,只能覆盖一个半区。考虑到6~16所对应的下浮率较小,从而对应的投标价较高,对应的利润也较高,显然博6~16所对应的半区更合算。另外,由于只要A级单位选择三数和为16所对应的下浮率,此时只要摇珠的三个球和不大于16,则A级单位中标(这里假设AA级单位都选取下浮率5.266 67%,其他单位没有选择三数和不小于16所对应的下浮率的情况)。因为此时如果摇珠的三数和为16时,A级单位不扣分,而AA级单位扣分超过0.8分,从而A级单位总分超过AA级单位的总分。如果摇珠的三数和小于16,假设A级单位在摇珠方面的扣分为a分,则AA级单位在摇珠方面的扣分超过(0.8+a)分,从而A级单位总分还是超过AA级单位的总分。
但是,如果A级单位选择三数和为17所对应的下浮率,则不管下浮率如何抽取,A级单位都不可能中标。因为类似上述情况的讨论,此时如果摇珠的三数和不超过17,则AA级单位和A级单位的总分相同,但AA级报价更低,所以AA级单位中标。
从而,A级单位博上半区应该选择的最佳下浮率为三数和16对应的下浮率,即4.433 3%,此时A级单位可以覆盖三数和从6~16所对应的下浮率,胜率为67/1 330=5.038%。
类似地,如果A级单位博50~60所对应的下半区,则A级单位最佳选择为三数和为49对应的下浮率5.533 3%。因为此时如果摇珠的三数和超过48,则AA级单位和A级单位的总分相同,但A级报价更低,所以A级单位中标。这时,A级单位的胜率为83/1 330=6.241%。综上所述,从胜率而言A级单位应该选择下浮率5.533 3%,此时胜算达6.241%,但对应的利润较低;而虽然选择下浮率4.433 3%,此时胜算达5.038%,但对应的利润较高。这就需要A级单位在利润和胜率两者之间做一均衡。
3 实例分析
2013 年广东某高速公路某合同段,招标人提前公布投标人的控制价为661 830 393元和下浮率范围为4.0% ~6.0%。该标共有10家单位参与竞标,其中AA级单位1家,A级单位5家,B级单位4家。
现场通过摇珠分别摇出号码3,2,11。下浮率为4.433 3%。
从而,最高投标限价为661 830 393×(1-4.433 3%)=63 248 924元,评标基准价为63 248 924×98%=619 839 461元。
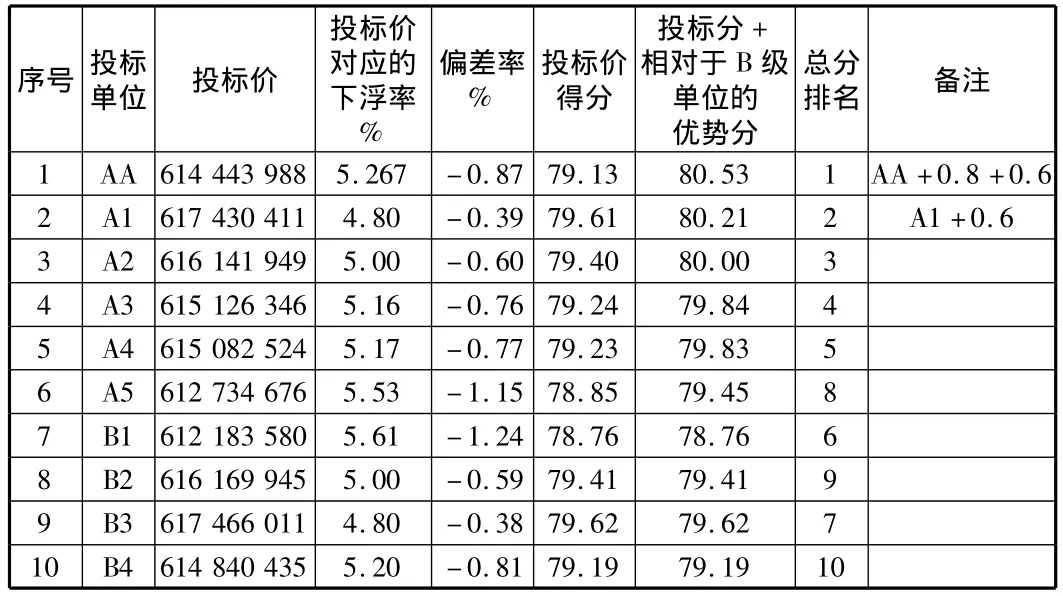
表2 各投标单位投标结果分析表
从表2实例结果来看,AA级单位投标价按照下浮率5.266 7%得到,根据我们上面所进行的分析,这是AA单位的最佳策略。在此策略下,该单位的赢面能够达到88.7%。此时,A级单位最佳应对策略应该在下浮率4.433 3%和5.533 3%选择。我们可以看到,只有A5理性地选择5.333%的下浮率,但是运气不好。其他的A级单位没有一家能够选择4.433 3%的下浮率。事实上,如果有一家A级单位选择4.433 3%的下浮率的话,此时该A级单位在摇珠得分方面不扣分,其投标分加上相对于B级单位的优势分为80.60分,超过AA级单位。
4 结语
投标报价是一门学问,基于随机原理的综合评估法虽然有一定的随机性,但其中不乏科学奥妙。正如中国科学院院士严加安在《悟道诗》所述:随机非随意,概率破玄机。本文正是利用概率统计的方法,较深入地分析了综合评估法,希望能够为有关单位的竞标提供一些建议和思考。

