大斜度四面体网格在高升力构型中的应用

肖中云，刘 刚，周 铸，江 雄

（中国空气动力研究与发展中心，四川 绵阳621000）

0 引 言

大型客机和军用运输机设计关键技术之一是起飞和着陆状态下的机翼高升力构型气动设计，要求在着陆状态下获得高升力，起飞状态获得高升力和低阻力。在飞机设计阶段，计算流体动力学（CFD）分析起到关键的技术验证作用。高升力构型下机翼前缘缝翼向下向前伸展，后缘富勒襟翼后退展开，增升部件打开留下的空隙和支撑机构完全暴露在气流当中，出现流动分离、边界层掺混等复杂流动现象，给CFD数值模拟带来很大挑战。

高升力构型的CFD数值模拟经过多年的发展，在多段翼型、机翼增升装置和全机模拟上都得到了应用，文献［1］指出现有CFD手段尚很难准确模拟高升力构型的最大升力系数及失速攻角，特别是对于存在明显分离区的复杂流动。准确预测分离流动的开始和发展，以及雷诺数效应依然是CFD的难点之一。在网格方法上，结构网格的模拟历史较长，文献［2］采用了多块对接网格模拟了梯形机翼高升力构型，文献［3］采用结构重叠网格模拟了波音777－200飞机着陆构型，不足之处是在处理复杂结构的时候网格生成难度极大，网格生成时间占计算周期的70%以上。非结构网格具有对复杂外形适应性强的特点，可以实现网格的自动生成，文献［4］采用非结构网格方法模拟了高升力构型复杂绕流，模拟包括了襟翼托架、凹槽、缝隙等细小结构，发挥了网格在处理复杂外形方面的优势。当然非结构网格也存在缺点，如存储量较大等，新的计算方法在不断的发展和完善当中［5－7］。

本文工作在“航空CFD可信度开放式专题研究活动”支持下得到开展，计算外形为NASA高升力梯形机翼构型，网格划分采用全四面体粘性非结构网格，为了模拟粘性效应，物面附近采用层推进方法生成大伸展比边界层网格。流场计算采用了基于消息传递（MPI）的并行分区计算方法，通过数值计算分析了高升力构型的升阻力系数和力矩系数的变化规律，并通过试验数据进行验证，考察了计算的网格收敛性质，最后指出数值模拟中存在的不足和改进方向。

1 计算方法

流动控制方程为雷诺平均N－S方程，湍流模型采用Spalart－Allmaras一方程模型，湍流模型和主控方程之间为松耦合。在计算方式上采用了基于消息传递（MPI）的分区并行计算方法，控制方程的时间积分采用LU－SGS隐式方法，单元面通量计算采用Roe通量差分分裂格式，二阶精度通过原始变量的线性重构获得，并采用Barth－Jespersen限制器使格式保持单调性。

1.1 单元线性重构

有限体积离散采用基于格心的离散格式［8］，这样守恒率方程表述为格心流场变量的时间变化与边界面通量之间的关系。为了计算边界通量，首先需要得到边界面的流场变量。假设流场变量在各网格单元内是分片线性分布，则面心的流场值可以表示为格心值和其梯度的表达式。

为此，梯度计算的格式选择尤为重要。对于格心离散格式来说，目前发展的梯度计算方法主要分为最小二乘法和基于节点平均方法两类［9］。最小二乘法在控制单元周围选取一定数量相邻单元作为梯度计算的模板，算法采用最小二乘法。模板选择可以是面相邻单元、点相邻单元和介于两者之间的选取模式，对于四面体网格来说，面相邻单元只有4个，点相邻单元有几十个之多，不同选取模式之间计算量差别很大。本文采用基于节点平均的梯度计算方法，模板单元如图1所示，首先将格心流场变量平均到格点，再用格点平均得到面心，格心流场变量的梯度由在单元体上运用格林－高斯公式得到。

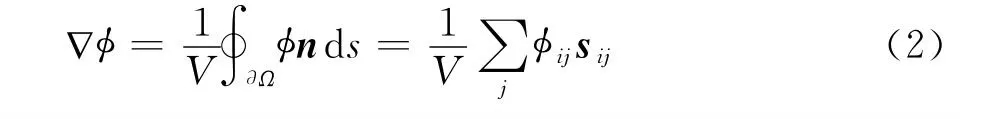
这样在计算格心梯度的时候，其计算模板间接包括了与其共节点的所有相邻单元。

图1 格心计算格式的模板单元Fig.1 Stencils of cell centered scheme

公式（2）适用于任意形状单元，对于单形网格单元（如四面体、棱柱、六面体等），边界面流场变量可以表示成格心和格点值的简单表达式［10］，其格心梯度在实质上等同于式（2）。式（1）中α代表限制器函数，目的是为了在单元重构中不出现新的极值点，满足计算格式的保单调性要求。本文采用Barth－Jespersen［11］提出的非结构网格的斜率限制器，该方法限制边界面上的重构值不超出该单元所有紧相邻单元（包括单元本身）的最小值和最大值范围。具体表达形式如下：

1.2 关于大伸展比拉伸网格

为了模拟粘性效应，网格生成通常沿物面或尾迹层生成大伸展比的拉伸网格，如图2所示，为此网格单元在流向和法向上的尺度可能相差几个量级。举例来说，如果网格单元的高宽比h／L＝1∶100，此时对应的最小内角＝tg－1（1／100）＝0.57°，也就是说在粘性四面体网格中存在大量的这种尖劈形网格单元，需要在计算方法上慎重处理。

图2 用于粘性计算大伸展比拉伸网格Fig.2 High aspect ratio meshes for viscous effect

式（2）中要用到面心的流场变量值φij，最简单的方法是取相邻单元格心值的平均，该方法的优势在于构造简单，不需要新增加数据结构，易于在复杂网格单元中实现。对高斜度的非结构网格来说，相邻格心的连线不通过面心，所以这种简单平均的方法存在误差，并且斜度越大误差越大，以图2所示的四面体拉伸网格可以看到，面心a与格心连线ij相差很远，所以在各向异性的非结构四面体网格中不能采用这种近似算法，而应代之以上节介绍的最小二乘法或基于节点平均的方法。

在应用限制函数的时候，最传统的做法是用两侧单元的流场值对边界面重构值进行限制，避免重构产生新的极值点。同样因为格心连线与面心距离很远的缘故，这种方法不能适用于粘性四面体网格，Barth－Jespersen斜率限制器提出用单元所有紧相邻单元（包括单元本身和面相邻单元）的最小值和最大值作为限制范围，放宽了限制条件，避免限制过大带来较大的数值耗散。

1.3 网格并行分区

计算外形为NASA高升力梯形机翼全展长襟翼模型［12］，该机翼没有扭转、没有上反角，采用了大弦长和相对较小展弦比（AR＝4.56），目的是获得较高的试验雷诺数。该构型为典型的着陆构型，前缘缝翼与后缘襟翼的偏角分别为30°和25°。模型平均气动弦长c＝1.0058m，半展长2.1615m，半模参考面积2.046m2，襟翼弦长和缝翼弦长分别为0.3m和0.127m。参考的风洞试验是1998年在NASA Ames 12英尺增压风洞（PWT）中完成的。

计算网格为全四面体非结构网格，网格在物面附近采用“层推进”方法生成的大伸展比拉伸网格，控制参数包括第一层网格物面距离、生长比、最大推进层数等，网格的法向尺度异于其他两个方向，又称为各向异性网格。第一层网格点的物面高度为2.5×10－5m，满足格心的无量纲高度y＋≈1。粘性层网格的生长比1.25，计算域的远场边界取为100倍平均气动弦长。

为了评价计算结果的网格收敛性，在同一外形上生成了粗网格、中等密度网格和密网格。表1给出了三套网格的对比，三套网格的第一层网格高度、生长比、远场边界等参数保持不变，主要差别体现在物面的网格密度不同，如图3所示。图4给出的是中等密度网格在机翼截面上的网格分布，从中可以看到沿物面法向生成的是大伸展比拉伸网格，目的是满足粘性附面层计算的要求；此外，网格在缝翼和主翼之间分布合理、光滑过渡，基本上满足高升力构型复杂空间流场对网格的要求。并行计算采用了Metis分区软件［13］对网格进行分区，目标是保证各分区间负载平衡和通信量最小，以中等密度网格下32个分区为例，每个分区的网格单元数383016个，相差只有1个单元。信息交换量可以用每个分区的分区边界面个数表示，其平均值为11696个，最大相差56%。图5给出的是物面和对称面上的网格分区情况，分区对接面传递信息包括对接单元和对应顶点的流场信息，在对接面上的流通量保持守恒。

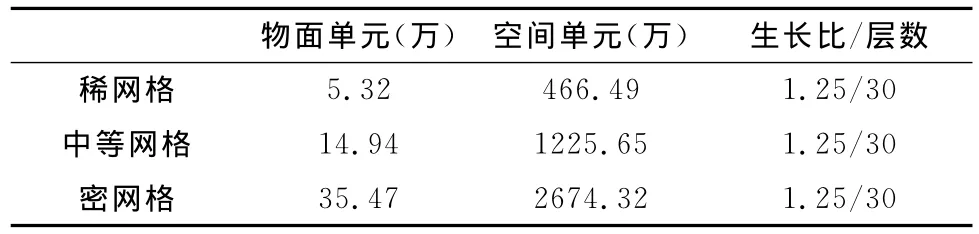
表1 稀网格、中等网格和密网格比较Table 1 Comparison of coarse，medium and fine grids

图3 三种网格在翼尖附近的比较Fig.3 Surface grid comparison at wing tip

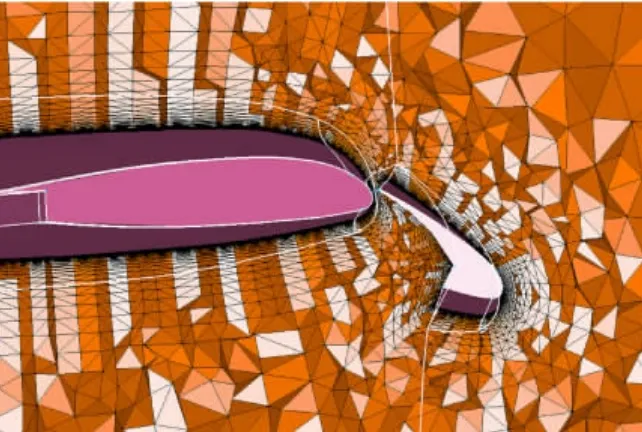
图4 机翼横截面上的网格分布Fig.4 Grid distribution on wing’s cross section

图5 并行计算的网格分区Fig.5 Grid partition for parallel computation

2 计算结果与分析

计算状态选择与试验条件相同，马赫数M＝0.15，攻角α＝－3.4°～36°，基于平均气动弦长的雷诺数Re＝1.5×107，流动假设为全湍流。图6给出的是采用中等密度网格计算得到的极曲线与试验值的比较，从图中可以看到，在所有计算点上计算值与试验值基本吻合一致，不足是在高升力状态下升阻比的计算值略低于试验值，在低升力状态下也存在一定偏差。在α＝11.02°时还分别用稀网格和密网格进行了计算，可以看到三种网格得到的升力系数和试验值都比较一致。图7给出的是俯仰力矩系数随升力系数变化曲线与试验值的比较，可以看到本文得到的俯仰力矩系数变化规律和试验值比较一致，但在量值上存在差别，在升力系数（1.5＜CL＜2.5）范围内预测的力矩系数绝对值比试验值偏小。从单个点上稀网格和密网格的计算结果来看，网格加密使计算值更接近于试验。

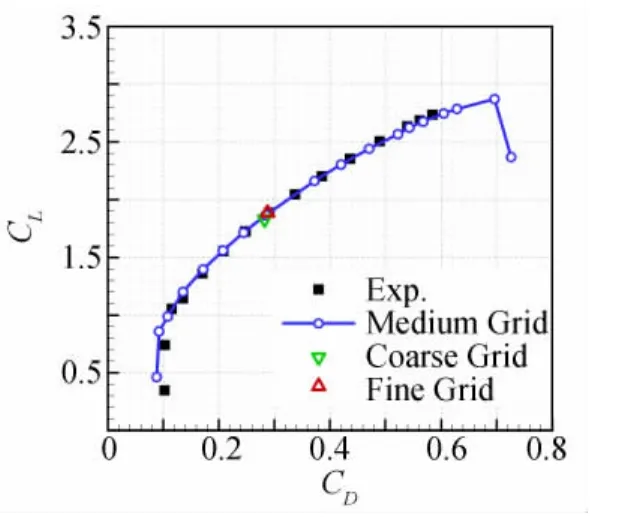
图6 极曲线与试验值的比较Fig.6 Polar curve compared with experimental data

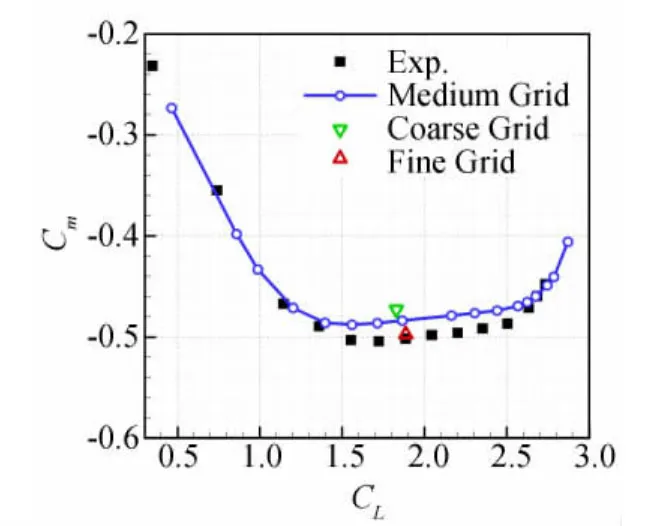
图7 俯仰力矩系数与试验值比较Fig.7 Pitching moment compared with experimental data

图8给出的是攻角α＝11.02°时的物面压力云图和流线分布，可以看到当前状态下襟翼后缘开始有分离出现，并且在机翼翼尖存在强烈的翼尖涡流动，给翼尖区域的准确数值模拟带来一定的难度。

图8 物面压力云图与流线分布（α＝11°）Fig.8 Wall pressure contour and streamlines（α＝11°）

图9给出了机翼不同展向截面上的压力系数分布与试验值的比较，其中计算网格采用中等密度网格，横坐标表示测压点位置（为和试验一致单位用英寸表示），缝翼和襟翼位置为展开状态下的坐标值，展向站位表示为机翼截面横向坐标与半展长的比值。从图中可以看到，在前面四个站位上压力系数的计算值和试验值都吻合较好，准确反映了各气动部件的负压峰值及压力突变位置，并且在一些复杂流动区域（如前缘缝翼的内凹区域、主翼后缘存放襟翼的区域）计算值和试验也基本一致。在第4个截面位置（η＝0.95）上，后缘襟翼的负压峰值明显低于试验值，主翼的后半段背风区的压力也出现偏差，其主要原因是在靠近翼尖位置存在有强烈的翼尖涡流动，在翼尖集中涡的影响下，上表面负压增加，襟翼的负压峰值显著上升，本文在数值模拟中存在对集中涡数值耗散过大的缺陷，即数值模拟得到的涡强度偏小，相当于弱化了集中涡的影响，导致上翼面的压力系数预测偏低。

图9 机翼Y向截面上的压力系数分布比较（α＝11.02°）Fig.9 Comparison of Cpdistribution on cross sections（α＝11.02°）

以攻角α＝11.02°为例，本文采用三种不同密度网格分别对流场进行了模拟，以探讨数值计算的网格收敛性。其中稀网格、中等网格和密网格分别对应4.66M、12.26M和26.74M空间单元，图10给出的是升力系数和阻力系数随网格规模的变化曲线，横坐标用网格指数（网格单元数的－2／3次方）表示，图中直线表示试验值。从图上可以看到，在固定攻角下，升阻力系数的计算值比试验值偏小，随网格密度增加，差距缩小，计算值逐渐靠近试验值。对于该图形来说，越靠近横轴左侧网格密度越大，如果沿变化曲线画一条趋势线，则趋势线与纵轴的交点代表网格无穷大时的计算值，称此时对应的计算解为网格无关解。从图10来看，升阻力系数并不完全随网格指数线性变化，说明计算网格还没有达到求网格无关解的要求。从图9可以看到，在展向截面靠近翼尖位置（η＝0.95），计算的压力系数较试验值偏小，主要原因是翼尖位置的空间网格密度不够，不能准确预测翼尖涡的影响。对于非结构网格来说，空间网格是自动填充而成的，其网格密度比较不易进行控制，这也是非结构网格面向工程应用需要解决的关键问题之一。

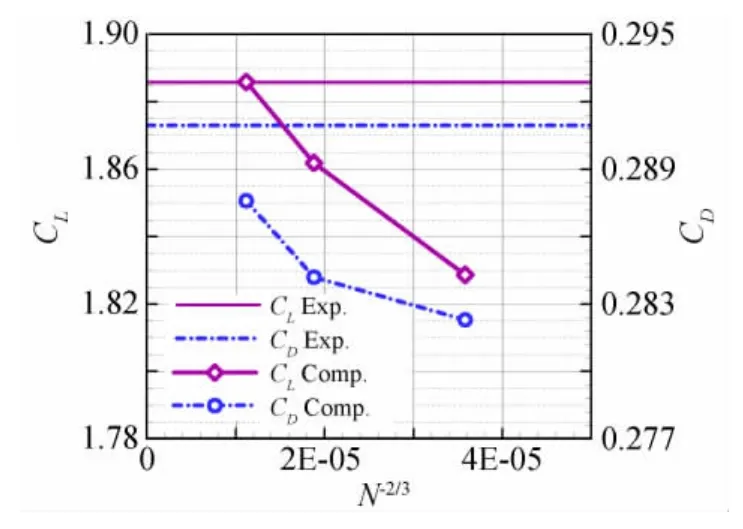
图10 升力和阻力系数的网格收敛性Fig.10 Grid convergence of lift and drag coefficients

3 结 论

基于全四面体粘性非结构网格，采用格心格式求解雷诺平均N－S方程，对梯形机翼高升力构型流场进行了数值模拟，计算结果通过试验数据进行了对比验证，得到结论如下：

（1）高伸展比粘性四面体网格存在面心与相邻单元格心不共线的特点，在面心流场变量重构当中，限制器函数不能仅用到相邻单元的格心值进行限制，否则会带来限制过强的问题。

（2）数值计算结果与试验数据基本一致，验证了本文方法的可行性，同时数值计算还存在翼尖涡数值耗散过大的问题，影响了翼尖区域压力分布的预测精度。

（3）非结构网格面向工程应用需要解决好空间网格不易控制的问题，提高分离涡模拟的精度。

［1］朱自强，陈迎春，等.高升力系统外形的数值模拟计算［J］.航空学报，2005，26（3）：257－262.

［2］王运涛，洪俊武，等.采用TRIP软件数值模拟梯形翼高升力构型［C］.中国航空学会2009年学术年会，北京：中国航空学会，2009.

［3］ROGERS S E，ROTH K.Advances in overset CFD processes applied to subsonic high－lift aircraft［R］.AIAA Paper 2000－4216，2000.

［4］CHAFFIN M S，PIRZADEH S.Unstructured Navier－Stokes high－lift computations on a trapezoidal wing［R］.AIAA Paper 2005－5084，2000.

［5］DISKIN B，THOMAS J L.Comparison of node－centered and cell－centered unstructured finite volume discretizations：inviscid fluxes［J］.AIAAJournal，2011，49（4）：836－854.

［6］BERGER M，AFTOSMIS M J.Analysis of slope limiters on irregular grids［R］.NAS Technical Report，NAS－05－007，2005.

［7］RUMSEY C，SUSAN X Y.Prediction of high lift：review of present CFD capability［J］.ProgressinAerospaceSciences，2002，38：145－180.

［8］BLAZEK J.Computational fluid dynamics：principles and applications［M］.Elsevier publisher，2001.

［9］MAVRIPLIS D J.Unstructured mesh discretizations and solvers for computational aerodynamics［R］.AIAA Paper 2007－3955，2007.

［10］FRINK N T.Recent progress toward a three－dimensional unstructured Navier－Stokes flow solver［R］.AIAA Paper 1994－0061，1994.

［11］BARTH T J，JESPERSEN D C.The design and application of upwind schemes on unstructured meshes［R］.AIAA Paper 1989－0366，1989.

［12］JOHNSON P L，JONES K M，MADSON M D.Experimental investigation of a simplified 3Dhigh lift configuration in support of CFD validation［R］.AIAA Paper 2000－4217，2000.

［13］KARYPIS G，KUMAR V METIS.A software pachage for partitioning unstructured graphs，partitioning meshes，and computing fill－reducing orderings of sparse matrices，version 4.0［M］.University of Minnesota，1998.