基于替代模型的三维后体尾喷管优化设计

苗 萌，曾 鹏，阎 超

（1.北京航空航天大学 国家计算流体力学实验室，北京 100191；2.北京临近空间飞行器系统工程研究所，北京 100076；3.中国航天电子技术研究院无人机系统工程研究所，北京 100094）

0 引 言

以吸气式冲压发动机为动力的飞行器将成为本世纪航空航天技术的发展方向和里程碑。自20世纪50年代以来，美国与前苏联就开展了这些方面的基础研究，80年代以后，欧洲、日本也逐渐加入到研究行列。X－43A、X－51A等试飞成功，更是预示着国外在高超声速飞行器领域取得了相当大的成果。为了确保我国在该领域达到国际先进水平，如何解决高声速飞行器气动设计问题显得尤为重要。与常规的亚声速、低超声速飞行器的设计不同，吸气式高超声速飞行器的机体与推进系统必须进行一体化优化设计［1］，而其后体尾喷管是飞行器产生推力、升力的关键部件，在一体化设计中占重要地位。

国内外对于吸气式高超声速飞行器后体尾喷管优化设计都做过相应的研究。对于二维平面或轴对称外形的尾喷管常采用特征线法进行设计，但应用于三维外形则过为复杂，且没有考虑粘性影响。20世纪70年代，Edwards C L Q等［2］将后体简化为斜平面，以喷管推力系数尾性能目标，完成了尾喷管简化构型的优化设计；Baysal O，Burgreen G W 等［3］将CFD技术引入尾喷管的优化设计领域，以轴向推力为目标，对二维喷管构型进行优化；罗世彬等［4］人基于二次和三次型线利用响应面和多目标优化方法，实现了二维构型的多目标优化；陈兵等［5］采用空间推进方法求解层流PNS方程，对二维尾喷管进行了优化设计；甘文彪等［6］结合试验设计方法、替代模型等技术通过求解RANS方程对二维后体尾喷管进行了多点多目标优化设计。贺旭照等［7］采用采用空间推进解算器求解超声速无粘流动，在二维尾喷管优化设计的基础上，确定了对称面的外形，并依此进行三维拓展，实现了三维后体尾喷管优化设计。

为了更加充分地挖掘后体尾喷管流动的三维膨胀性能，本文直接将尾喷管三维外形参数化并通过CATIA二次开发［8］使参数化外形生成自动化，通过求解层流NS方程模拟考虑粘性的真实情况，为降低计算量利用了试验设计方法对样本点在设计空间内抽样并进行CFD计算，依此构建Kriging模型［9］来代替优化过程中海量的CFD计算，优化算法采用NSGAⅡ［10－11］多目标遗传算法，对后体尾喷管三维构型进行了优化设计，并对优化出的结果进行了CFD计算验证。

1 优化方法

基于替代模型的气动优化设计需要有四大技术作为支撑：高精度的CFD求解器、高效可靠的替代模型、高效且方便的现代优化算法、对优化外形的参数化建模及CFD计算网格的自动生成。

1.1 CFD求解器

本文采用课题组编写的CFD求解器进行CFD计算，该求解器已经在多项科研及工程项目中得到成功应用。通过求解三维可压全N－S方程来获得尾喷管的推力和升力：

式中，Q为守恒变量，F、G、H分别为三个方向上的无粘通量，Fv、Gv、Hv分别为三个方向上的粘性通量。

空间格式采用高分辨率的Roe的FDS格式，时间格式为高可靠性、高效率的LU－SGS格式。

1.2 Kriging模型

Kriging模型是一种全局替代模型。通常Kriging模型包括两部分，具体模型为：

式中：f（x）是对全部设计空间的全局模拟，可看作一个常数β，β值可由已知响应值进行估计，z（x）是期望为0、方差为σ2的高斯随机函数，表示全局模拟的插值。z（x）的协方差矩阵可表示为：

式中：R为相关矩阵；R（xi，xj）为相关函数；i，j＝1，2，…，n。n为已知的样本中数据的个数，其表达式为：

式中：nk为设计变量的个数；θk为未知的相关参数矢量。一般地可用标量θ来代替θk。

根据Kriging理论，未知点x处的响应值y的估计值可通过下式给出：

式中：y为样本的响应值；f为长度为n的单位列向量；rT（x）为未知向量x与样本输入数据之间的相关向量［x1，x2，…xn］，表达式为：

相关系数θ可以由极大似然估计给出。

1.3 NSGAⅡ多目标遗传算法

NSGAⅡ在2002年提出。与基本遗传算法相比，NSGAⅡ在适应度计算方面主要有非支配排序及拥挤度排序这两个特性。非支配排序使处于前缘的个体具有更大的概率被选中执行交叉变异等操作进入下一代；拥挤度排序使个体分散更加均匀，并能更好地保持解的多样性。NSGA II中，对每个解来说，需要确定多少解支配它和它支配的解集。NSGA II需要估计围绕着种群中一个特定解的解密度，即沿着问题的每个目标计算两个解之间的平均距离，这个值被称为密集距离（crowding measure）。在选择期间，NSGA II密集比较算子既考虑种群中个体的非劣解秩，也考虑密集距离。也就是说，优先选择非劣解；但当两个解具有相同的非劣解秩时，则选择那个不处于拥挤距离区域内的解。与其它多目标遗传算法相比，NSGA II的精英保留策略使用（μ＋λ）选择，包含了最好的父代和子代个体。正是这种机制使新一代种群比前一代种群更有效，效果更好。本文采用ISIGHT软件包中的NSGAⅡ程序进行优化计算。

2 三维后体尾喷管优化设计

吸气式高超声速飞行器后体尾喷管要求有尽可能大的推力及升力，本文即选取推力及升力作为优化目标。首先对三维喷管外形进行参数化，并编制VB程序调用CATIA接口进行二次开发使外形生成自动化；计算网格采用Gridgen软件生成并通过其宏录制功能使网格生成自动化，结合高精度CFD求解器及NSGAⅡ多目标遗传算法对三维尾喷管进行优化设计。流动条件与文献［7］一致，喷流入口条件为：Ma＝1.2，静温T＝2170K，静压p＝0.195MPa；外部来流条件为：Ma＝6，静压p＝2978Pa，静温T＝235.45K，攻角4.5°。

2.1 三维外形参数化及CAD模型自动生成

尾喷管整体外形如图1所示，由内膨胀段（有下壁板）和外膨胀段（无下壁板）构成。对称面形状如图2所示，在对称面外形基础上，沿流向在对称面型线上定义一系列展向剖面线，就刻画出整个三维尾喷管上表面型线。

尾喷管总长L和喷管入口高度h确定，分别为850mm和64mm。对称面采用三次曲线的建模方式，三次曲线多变的外形及良好的适应性能较好地描述多样的喷管外形，燃烧室出口和喷管上表面用圆弧过渡，圆弧半径为R，即图中的圆弧AB。BC段为三次曲线，为保证曲线上凸，把C点配置为拐点。BC段与AB段在B点处以初始膨胀角θ1相切，三次曲线BC的出口角为θ2；喷管下壁板OE长度为Lb，OE与水平线夹角为θc。其中圆弧半径R，初始膨胀角与喷管出口角θ1、θ2，下壁板长度Lb、角度θc为变量，在确定变量之后，即可确定对称面的整体外形。

图1 三维尾喷管建模示意图Fig.1 CAD model of 3Dnozzle

图2 对称面外形及参数化Fig.2 Symmetry plane geometry map of 3Dnozzle

尾喷管内膨胀段（OE段）上壁面型线，通过对基准面型线展向延拓得到。在每一个展向剖面上，采用超椭圆定义展向剖面型线。图3为三维尾喷管展向剖面的建模示意图。

在图3中，以‘o’点为坐标原点的超椭圆函数可以表示为：

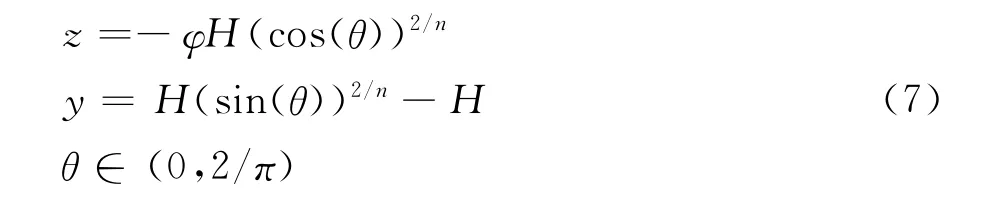
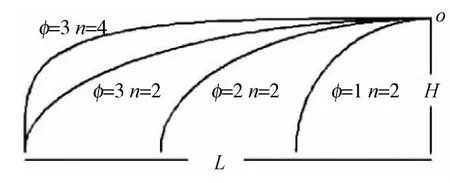
图3 三维尾喷管展向剖面Fig.3 Section plane curve of 3Dnozzle

其中L和H表示尾喷管型面在某个流向截面上的展向宽度和高度，L表示尾喷管侧缘距基准面的展向距离，H表示侧缘距基准面的法向距离，参数n可以控制超椭圆的弯曲程度，而φ＝L／H表示超椭圆的宽高比。同过以上的方程三维尾喷管展向截面的剖面线可以通过L，H，n这三个参数得到完全描述。L在尾喷管的内膨胀段和发动机入口处宽度相等，为150mm，在外膨胀段，喷管末端宽度定义为LL已知，为220mm。内膨胀段与外膨胀段通过一段圆弧过渡，圆弧半径为r，圆弧角为θ，圆弧与一段拐点配置在尾喷管末端且外凸的三次曲线相连。其中r和θ为设计变量。图4为展向宽度变化规律示意图。高度方面，在内膨胀段尾喷管的高度由下档板的位置确定，在外膨胀段沿流向的高度由以下公式确定：

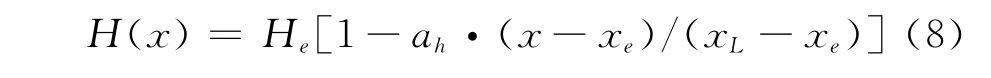
式中He为尾喷管内膨胀段结束处上下型面之间的高度，ah为一设计变量，决定侧壁高度的变化，ah越大，则侧壁高度随x增加而减小越快，当ah为0时，侧壁高度保持He不变。沿流向，喷管截面超椭圆曲线指数通过一下方程确定：

式中M为一正整数，本文取为200，c为一较小整数，本文取为3。an为设计变量，确定展向截面的形状，an越大则展向截面越接近于矩形。通过上面的型面建模过程，三维尾喷管的型面可以由完全由θ1、θ2、θc、R、Lb、r、θ、ah、an九个参数描述，其中前五个为二维对称面的参数，后四个为向三维延拓后所增加的参数。九个参数的取值下限为［1°，1°，－10°，50mm，80mm，50mm，1°，0，0.01］，取值上限为［40°，40°，10°，500mm，250mm，200mm，10°，0.5，0.2］。原始外形的九个参数分别为［20°，20°，－3°，200mm，100mm，100mm，5°，0.2，0.1］。

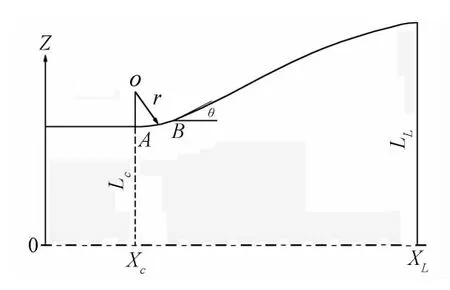
图4 三维尾喷管展向宽度变化规律Fig.4 Side wall width changing curve

在三维建模中，先根据具体外形在流向选定疏密适当的100个站位，而后根据读入的外形参数可计算得到该100个站位上展向切面上的控制型线，在每条控制型线生成21个控制点并连接为样条线，则半个上表面曲面即可采用这100条样条线结合为多截面曲面得到。在VB程序中，得到九个控制外形的参数后，即可计算得到个控制线上点的坐标，并调用CATIA接口将点连成线并最终生成曲面，实现外形生成的自动化。自动生成的半模外形见图5。

图5 采用CATIA二次开发自动生成的半模外形Fig.5 Half of the model automatically created by CATIA secondary development

2.2 计算网格及其自动生成

计算网格为分区对接结构网格，采用Gridgen软件生成，录制宏使网格生成自动化。由于考虑粘性流动，网格采用内O型拓扑以便于边界层的布置，网格见图6，共有8个分区，网格总数为217280。

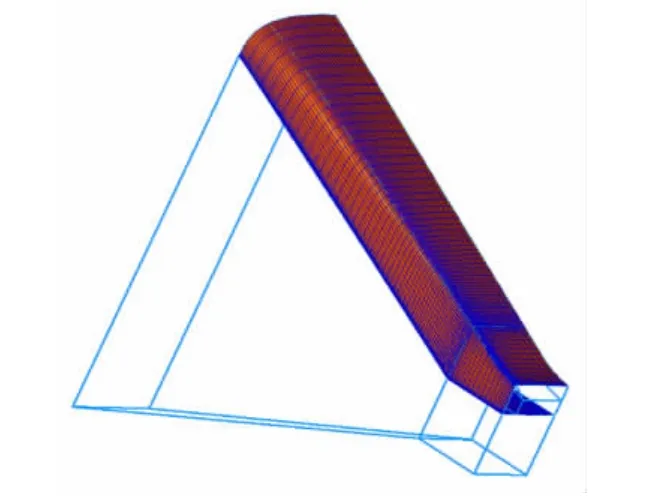
图6 Gridgen软件自动生成的计算网格Fig.6 Grid generated automatically by Gridgen

2.3 试验设计及Kriging模型构建

采用优化拉丁方方法［12］在整个设计区间内抽取100个样本点进行CFD计算得出其推力和升力，以此构建Kriging替代模型。优化拉丁方方法在随机拉丁方方法的基础上做了改进，使样本点散布更加均匀。为验证替代模型精度，在设计空间内再次随机抽取20个点分别采用CFD和替代模型计算以检验替代模型精度，结果如图7和图8所示，可见替代模型对升力FL的模拟效果好于对推力FT的模拟，替代模型的相对误差多在5%以内，最大不超过10%，替代模型精度满足使用要求。

2.4 多目标优化结果及分析

遗传算法参数选取为：实数编码，种群大小为100，遗传算法共计算100代；交叉操作采用单点交叉，交叉概率0.9，变异操作采用单点变异，变异概率为0.1。

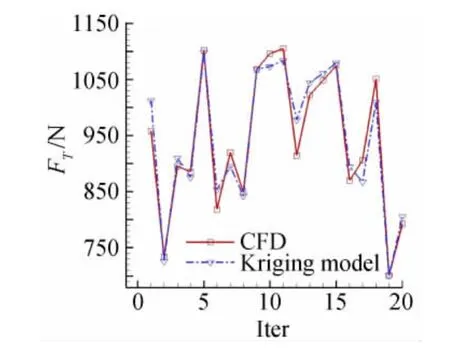
图7 CFD与Kriging模型计算推力结果Fig.7 Thrust computed by CFD and Kriging model

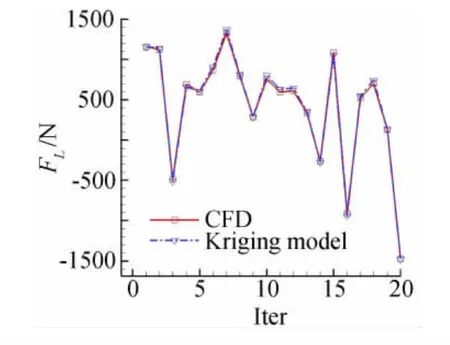
图8 CFD与Kriging模型计算升力结果Fig.8 Lift computed by CFD and Kriging model

图9为优化得到的Pareto前沿，并标明了原始喷管和选优喷管在Pareto前沿中对应的位置，可见Pareto前缘较为饱满，得到的优选喷管性能较原始喷管有了较大的提高。优选喷管的性能应保证推力和升力较原始喷管都有所提升，并综合考虑使喷管性能最优。由图9可见，原始构型的推力已足够大，若使推力有大幅度提升则会大大损失升力，因此所选择的优选构型推力仅有小幅度提高，但升力较原始构型提高了123.3%。优选喷管的九个参数为［17.65°，1.14°，－5.69°，211.68mm，199.92mm，70.03mm，1.36°，0.16，0.18］。由于这是替代模型得出的结果，再次对选优喷管进行CFD计算，结果见表1，可见两者相差不大，基于替代模型的优化设计达到了所期望的结果。

图9 多目标优化结果和Pareto前缘Fig.9 Multi－objects optimization result for 3Dnozzle

图10为原始外形与优选外形壁面等压力线图，可见优选外型较原始构型沿流向压力下降更缓慢，沿展向分布更加均匀。图11为原始外形和优化外形对称面等压力线图，可见优化外形内膨胀段较长，流动在下壁板出口处产生的膨胀波较原始喷管弱很多，因而使上壁面压力没有很快的下降，从而使升力大大增加。

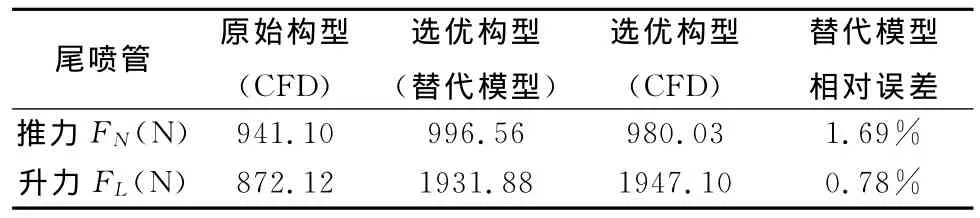
表1 原始构型与优化构型气动性能比较Table 1 Comparison between original and optimized 3Dafterbody nozzle

图10 原始尾喷管与优化尾喷管壁面压力比较Fig.10 Pressure contour comparison for optimization and original nozzle

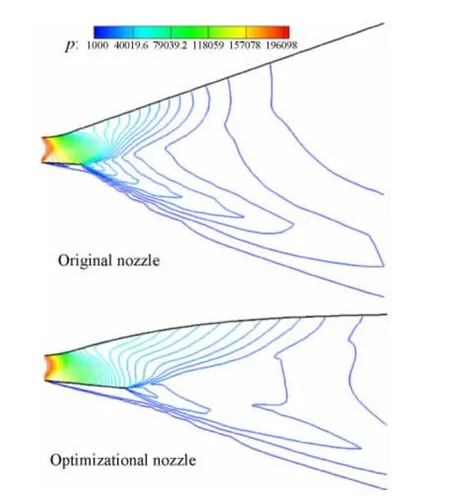
图11 原始尾喷管与优化尾喷管对称面流动等压力线图Fig.11 Pressure contour comparison of symmetry plane for optimization and original nozzle

本次优化工作在办公机上进行，使用单核CPU 2.4GHz进行计算。共进行CFD计算122次（构建替代模型100次、验证替代模型20次、原始及优化外形计算2次），每次CFD计算耗时30min，加上遗传算法运行时间10min，共耗时3670min。若不采用替代模型，优化过程共需进行CFD计算10000次，需耗时300000min，则优化工作根本无法进行。替代模型的引入大大缩短了优化过程所需时间；在精度上，由优化结果的CFD验证可以看出，替代模型的相对误差很小，精度满足要求。

3 结 论

本文通过试验设计方法抽取样本点进行CFD计算以构建替代模型来代替优化过程中的大规模CFD计算，在较短的时间内完成了吸气式高超声速飞行器三维后体尾喷管优化设计。在工程实际中，三维构型气动优化方法难以应用的瓶颈是复杂外形参数化及自动生成困难以及过大的计算量，本文的工作表明：

（1）采用CATIA二次开发能方便快捷地实现三维后体尾喷管参数化外形的自动生成，结合Gridgen软件的宏功能实现计算网格的自动生成，能高效地实现前处理的自动化，便于在工程中应用。

（2）使用优化拉丁方方法抽样来构建Kriging模型，能准确地模拟三维后体尾喷管在不同外形参数下产生的推力及升力，对非线性系统具有很好的模拟能力。

（3）基于替代模型的优化设计方法能大大缩短优化时间，高效地完成了三维后体尾喷管的优化设计，便于三维构型的优化设计工作广泛应用于工程实际。由于后体尾喷管为吸气式高超声速飞行器的一个部件，设计时必须考虑飞行器整体力矩平衡并兼顾各种性能，进一步的研究将进行三维机体／推进系统的一体化优化设计，即在本文方法的基础上，发展出一套对三维整机进行参数化的方法，并对其进行气动性能优化设计。

［1］李晓宇.高超声速飞行器一体化布局外形设计［D］.长沙：国防科学技术大学，2007.

［2］EDWARDS C L Q，SMALL W J，WEIDNER J P.Studies of scramjet／airframe integration techniques for hypersonic aircraft［R］.AIAA 75－58，1975.

［3］BAYSAL O，ELESHAKY M，BURGREEN G.Aerodynamic shape optimization using sensitivity analysis on third－order Euler equations［J］.JournalofAircraft，1993，30（6）：953－961.

［4］罗世彬.高超声速飞行器机体发动机一体化及总体多学科设计优化方法研究［D］.长沙：国防科学技术大学，2004.

［5］陈兵.空间推进算法及超燃冲压发动机部件优化设计研究［D］.北京：北京航空航天大学，2005.

［6］甘文彪，阎超.高超声速飞行器后体／尾喷管优化设计［J］.北京航空航天大学学报，2011，37（11）：1440－1445.

［7］贺旭照，倪鸿礼，周正，等.吸气式高超声速飞行器三维后体尾喷管优化设计［J］.推进技术，2009，30（6）：687－690.

［8］胡挺，吴立军.CATIA二次开发技术基础［M］.北京：电子工业出版社，2006.

［9］ALEXANDER I J fORRESTER，ANDY J KEANE.Recent advances in surrogate－based optimization［J］.ProgressinAerospaceSciences，2009，45（3）：50－79.

［10］SRINIVAS N，DEB K.Multiobjective optimization using nondominated sorting in genetic algorithms［J］.EvolutionaryComputation，1994，2（3）：221－248.

［11］DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multiobjective genetic algorithm：NSGAⅡ［J］.IEEETransactionsonEvolutionaryComputation，2002，6（2）：182－197.

［12］ANTHONY A G.Use of data sampling，surrogate models，and numerical simulation optimization in engineering design［R］.AIAA 2002－0538，2002.