不同厚度新月形覆冰对导线气动力特性的影响

楼文娟，林 巍，黄铭枫，沈国辉，陈 勇，闫 东

（1.浙江大学结构工程研究所，浙江 杭州 310058；2.河南电力试验研究院，河南 郑州 450052）

0 引 言

在一定的气象条件下，输电导线可能在其迎风面覆冰，具有翼形的某些特征，从而使受力情况变得复杂。在一定的风速和攻角下，导线容易产生舞动。舞动是输电导线的一种低频、大幅的自激振动。大幅度的舞动产生的反复动力冲击将导致塔臂和绝缘子的破坏及输电塔结构上横担和杆件螺栓的松动；导线舞动还将造成线路频繁跳闸与停电，对输电线路安全运行的危害很大［1］。

导线覆冰情况极其复杂，它与海拔高度、电线走向、风向、风速、气温等多种因素有关。常见的覆冰形式有雨淞、湿雪、干雪、霜淞、雾淞等五类［2］。其中，霜淞和雨淞两类覆冰附着力大，在雨淞地区，由于冻雨持续时间较长，可能形成较厚而坚实不易脱落的覆冰层，成为发生导线舞动的重大威胁。由于覆冰形状的随机性和多样性，目前国内外对覆冰导线的气动力研究只能选择具有代表性的典型覆冰形状进行研究。Mckay G A［3］，Kikuchi T［4］通过现场观测研究输电导线的覆冰形状。Yukino T［5］、肖正直等［6］通过试验研究了导线的覆冰形状。根据湖北中山口大跨越实际观测发现导线覆冰形状有如下规律［1］：气温较低，雨量较小，形成新月形；气温较低，雨量较大，风速一般，一般形成扇形；气温较低，雨量较大，风速较大，一般形成D型；气温较高，雨量较大，风速一般，形成垂挂的冰凌。日本学者M Masataka对124次舞动观测中的覆冰形状进行了归类［2］，结果表明，在实际舞动的观测中新月形覆冰占有相当大的比重。

覆冰导线气动力三分力系数是舞动分析计算的重要参数。这些参数可通过风洞试验［6－9］或CFD数值模拟［10－11］获得。但以往的试验主要针对单导线进行，因此，实际高压线路中常用的分裂导线气动力系数仍十分缺乏。且除文献［8］外，其他文献均在均匀流场中进行，实际线路中气流必然存在湍流的成分。CFD数值模拟与风洞试验结果相比只能在一定程度上反映覆冰导线的气动力特性，在某些风攻角下存在较大的误差。由于覆冰的随机性和多样性，已有的成果仍不能满足舞动研究的需要。积累不同厚度覆冰及覆冰分裂导线的气动力系数对研究导线舞动具有重要的学术与应用价值。

本文制作了4种不同覆冰厚度的新月形导线节段模型，在5%的均匀湍流场中测试了4种不同覆冰厚度的单导线及二、四分裂导线的气动力特性。研究了覆冰厚度对气动力特性的影响。分析了不同覆冰厚度导线的驰振稳定性，阐明了分裂导线气动力特性与单导线的区别。

1 试验概况

1.1 试验模型

根据实际输电线路导线截面尺寸，按1∶1的几何尺寸制作刚性模型。参考国标（LGJ GB117983）的型号规定，单导线通常选用 LGJ－240（φ21.6mm），本文为与分裂导线直径相一致以便于比较，将所有导线直径统一采用 LGJ－400／35（φ26.8mm），分裂导线间距相应进行放大，覆冰厚度对导线直径无量纲化。设计0.25D、0.5D、0.75D和1D等4种厚度的新月形覆冰，D为裸导线的直径。表1给出了覆冰导线试验模型的详细规格，试验模型截面如图1所示，模型长度取800mm。

表1 覆冰导线试验模型规格表Table 1 Specifications of test models

图1 不同覆冰厚度导线截面图Fig.1 Sections of conductor with different ice thickness

1.2 试验设备

试验在浙江大学边界层风洞（ZD－1）中进行。有关实测资料表明，发生舞动的风速多集中在7～15m／s，本次试验风场取风速为10m／s，湍流度为5%的均匀流。

均匀湍流场通过安装在风洞试验段入口处的多功能尖塔实现，如图2所示。

图2 均匀湍流场模拟Fig.2 Wind tunnel simulation of homogeneous turbulence

测力设备为德国 ME－SYSTEM公司生产的高频动态测力天平，数据采样频率达1000Hz，具有大小两个量程。小量程水平力量程为20N，扭矩量程为4N·m；大量程下水平力量程为130N，扭矩量程为26N·m。测力精度3‰。本次试验单导线和二分裂导线选用小量程，四分裂导线则选用大量程。

试验时将高频测力天平中心与风洞的转盘中心保持一致，模型通过转接板与天平刚性连接。为消除导线端部流体分离影响，保证导线主体上的二元流动，导线模型上下两端设置表面光滑的端板，模型转接板与下端板之间不相碰。上端板与模型间保留微小缝隙使得上部端板的荷载不被传至天平。下端板抬高是为了考虑消除风洞底面的边界层效应。试验模型及装置照片如图3所示。风向角定义如图4所示，由于覆冰模型的对称性风攻角范围取为0°～180°，间隔为5°，对某些升力系数变化大的角度进行测试风向角加密。测量时天平的采样频率设为200Hz，每个攻角下采样时间30s。

2 试验内容

覆冰导线的气动力可表示为升力FL、阻力FD和扭矩M，如图4所示。将气动力无量纲化可得：式中CL、CD、CM分别为覆冰导线的升力系数、阻力系数和扭转系数。U为试验风速，ρ为试验时空气密度，l和A分别为模型的有效长度和有效迎风宽度，B为分裂导线的间距。对单导线：A＝B＝D＝0.0268m；对二分裂导线：A＝2D＝0.0536m，B＝0.448m；对四分裂导线：A＝4D＝0.1072m，B＝0.45m。

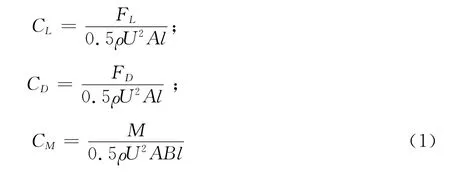
图3 风洞试验模型及装置Fig.3 Conductor model setup in the wind tunnel

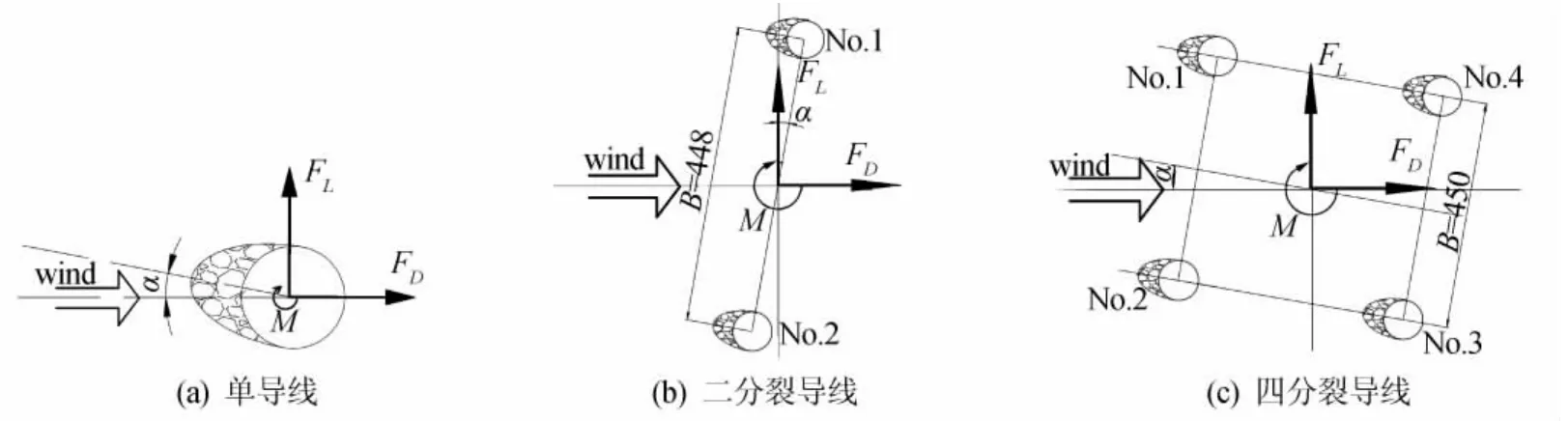
图4 气动三分力方向及风攻角定义Fig.4 Definition of aerodynamic force direction and wind angle

试验所测得的力为随风洞转盘转动的天平坐标轴下的X、Y轴力，需将各风攻角下天平轴下的气动力转化为气流轴下的升力和阻力。将高频天平测到的气动力时程进行时均化处理，最终通过式（1）计算得到所需的动三分力系数。

3 覆冰导线气动力特性试验结果

3.1 单导线气动力特性

不同覆冰厚度下单导线的气动力系数如图5所示。升力系数由正到负呈正弦状变化，随着覆冰厚度的增加，曲线两侧在15°和170°附近出现尖峰。1D厚度覆冰在小攻角范围内的峰值大于0.75D厚度覆冰，而在大攻角范围内的峰值，0.75D却比1D厚度的高，这表明，随着覆冰厚度的增大，到特厚覆冰时升力系数曲线变化规律会有局部的变化。由于覆冰的对称性，0°和180°风攻角下升力系数接近于零。

阻力系数在0°～180°之间呈半波状分布，两端小中间大，这与导线实际投影面积的变化有关。随着覆冰厚度的增大，相应攻角下阻力系数绝对值变大。厚覆冰时，在升力系数出现尖峰的攻角处（15°～20°），阻力系数曲线也出现拐点。

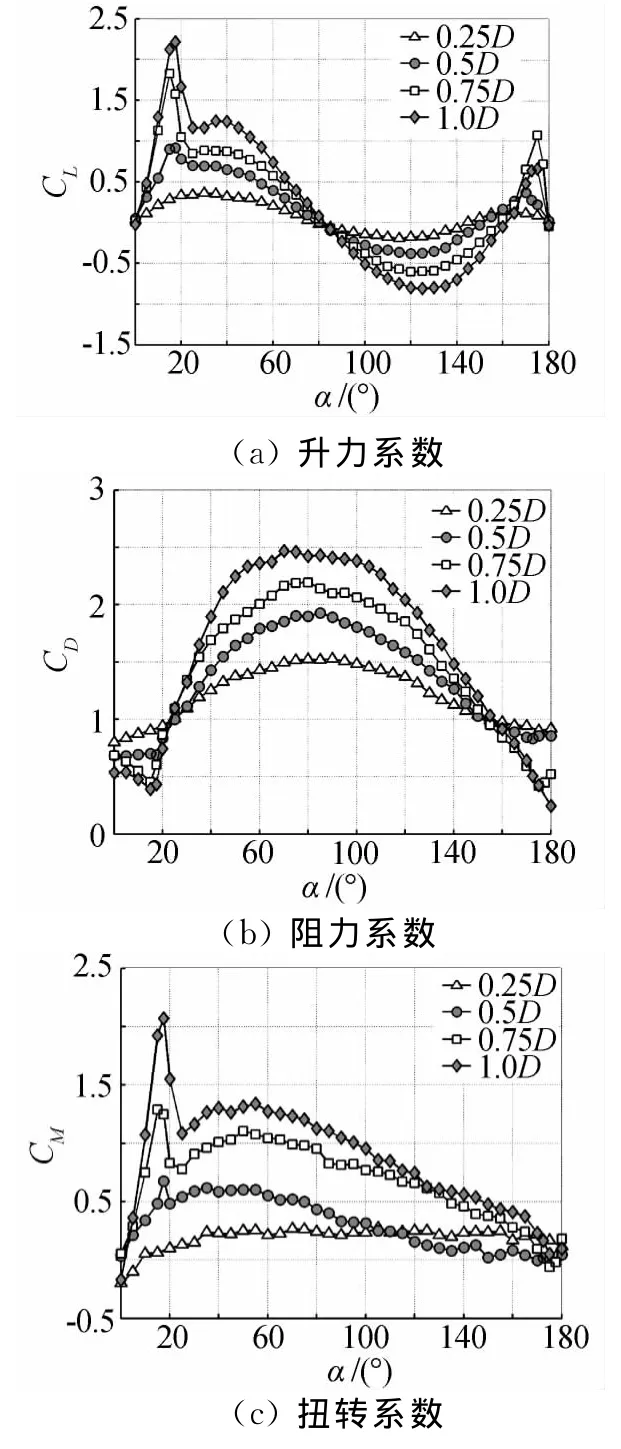
图5 覆冰单导线的气动力系数Fig.5 Aerodynamic force coefficients of single iced conductor

扭转系数曲线同样由于覆冰的对称性，在0°和180°风攻角下接近于零。薄覆冰时导线截面接近圆形扭转系数较小，且随风向角变化不明显。随着覆冰厚度的增大，扭转系数明显加大，且在15°～20°之间有较大突变，出现尖峰。

3.2 分裂导线气动力特性

图6和图7分别给出了0.75D和1D模型的分裂导线气动力系数及其与单导线的比较。从图中可以看出，由于上风尾流的影响，二分裂导线的阻力系数在90°攻角附近相对单导线下降约20%，其他攻角下阻力系数与单导线相差不大。对四分裂导线来说，由于尾流的干扰，除90°攻角外，在45°及135°攻角下阻力系数也有较大幅度的下降，降幅约15%。对扭转系数来说，为方便与单导线比较，定义转化关系如下：

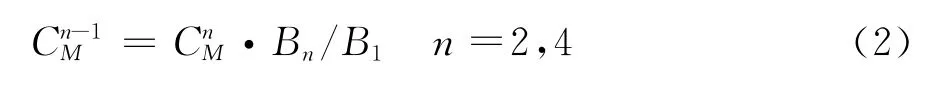
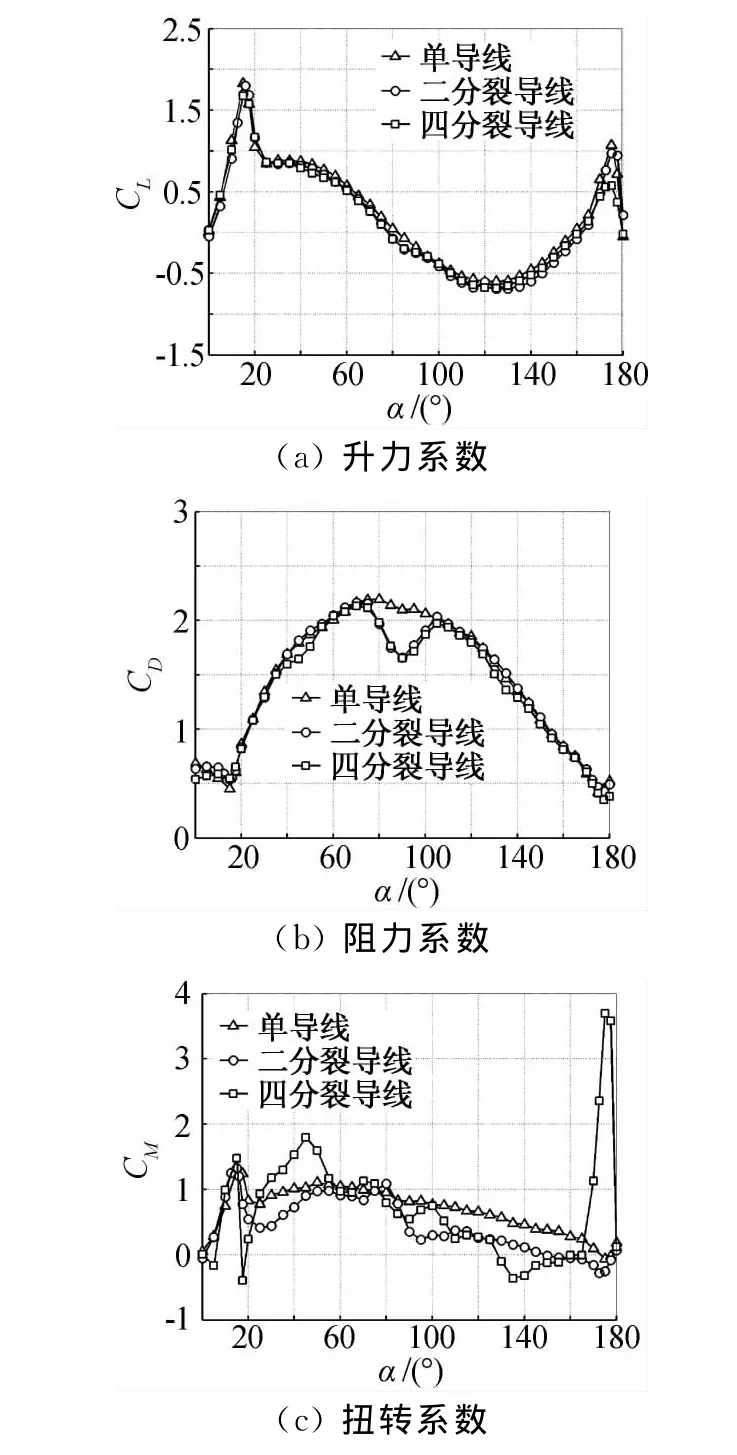
图6 0.75D厚覆冰分裂导线气动力系数Fig.6 Aerodynamic force coefficients of single and bundle 0.75Diced conductors

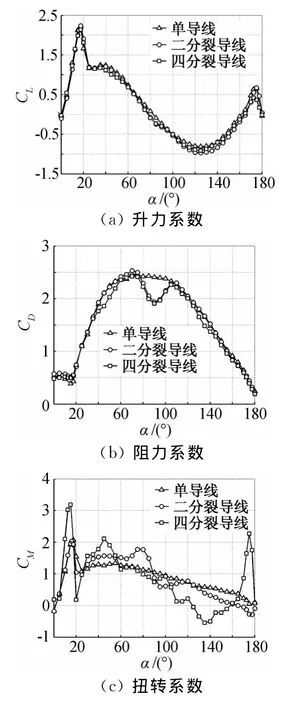
图7 1D厚覆冰分裂导线气动力系数Fig.7 Aerodynamic force coefficients of single and bundle 1Diced conductors

式中，和分别为分裂导线和分裂导线转化成相应单导线的气动扭转系数。B1和Bn分别为单导线和分裂导线的扭转特征长度。

从图6和图7可以的看出，分裂导线尤其是四分裂导线的扭转系数与单导线相差很大。这与尾流干扰导致各子导线的气动力特性差异有关。分裂导线的扭矩由三个部分组成，可表示如下：

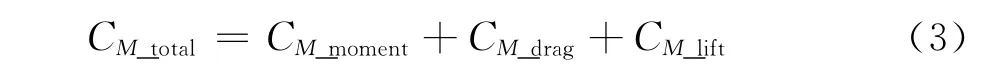
式中，CM＿total为分裂导线整体气动扭转系数，CM＿moment、CM＿drag、CM＿lift分别为子导线自身扭矩、阻力和升力对分裂导线整体气动扭矩的贡献。对四分裂导线来说，各分量可表示如下：

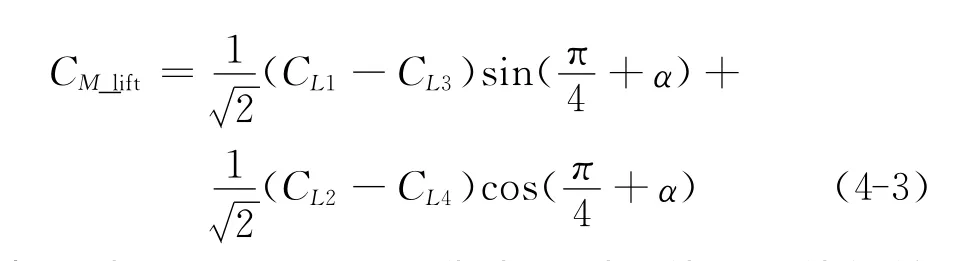
式中，下标i（i＝1，2，3，4）代表分裂导线子导线的编号，α为风攻角。

从式（4）中可以看出，分裂导线由于尾流的干扰，子导线间升力和阻力系数的差异对分裂导线整体扭转系数的影响是巨大的，因此分裂导线的扭转系数很难通过单导线来确定。由于测力设备的限制，可通过数值模拟等手段得到分裂导线各子导线的气动力，从而明确阻力和升力对整体扭矩的贡献。

3.3 驰振稳定性分析

根据Den Hartog驰振机理［12］，覆冰导线驰振稳定性可由下式判断：

式中，Den即为DenHartog系数。若Den小于零则导线将可能发生舞动。可以看出，影响Den Hartog系数的气动参数为升力与阻力系数。

根据Nigol舞动机理［13］，当覆冰满足某种特定条件时，扭转振动为自激振动，若导线的扭转频率和横风向自振频率接近，扭转振动就激发了导线的横风向振动。导线发生尼戈尔舞动的必要条件可用下式表示：

式中，C为覆冰导线的扭转系数称为Nigol系M数。对升力系数和扭转系数求导可得不同覆冰厚度下的Den Hartog系数和Nigol系数如图8～图10所示。

由图8可见，新月形覆冰单导线的不稳定攻角分别在15°～30°和170°～180°范围内。随着覆冰厚度的减小，Den Hartog系数绝对值变小，当为0.25D的薄覆冰时，全攻角的Den Hartog系数均大于零。理论上对于薄覆冰情况，根据Den Hartog竖向舞动机理导线将不会发生舞动。

对分裂导线来说，Den Hartog舞动的稳定区与单导线基本一致，而Nigol舞动的不稳定区有所不同。二分裂导线在80°～100°攻角范围内出现不稳定区，而原本对Nigol机理稳定的大攻角范围（170°～180°）在四分裂导线时变成不稳定区。

若考虑导线覆冰后重力偏心等因素的影响，导线将存在初始凝冰角，初始风攻角极易在15°～30°和170°～180°范围内出现，发生舞动的可能性较大。

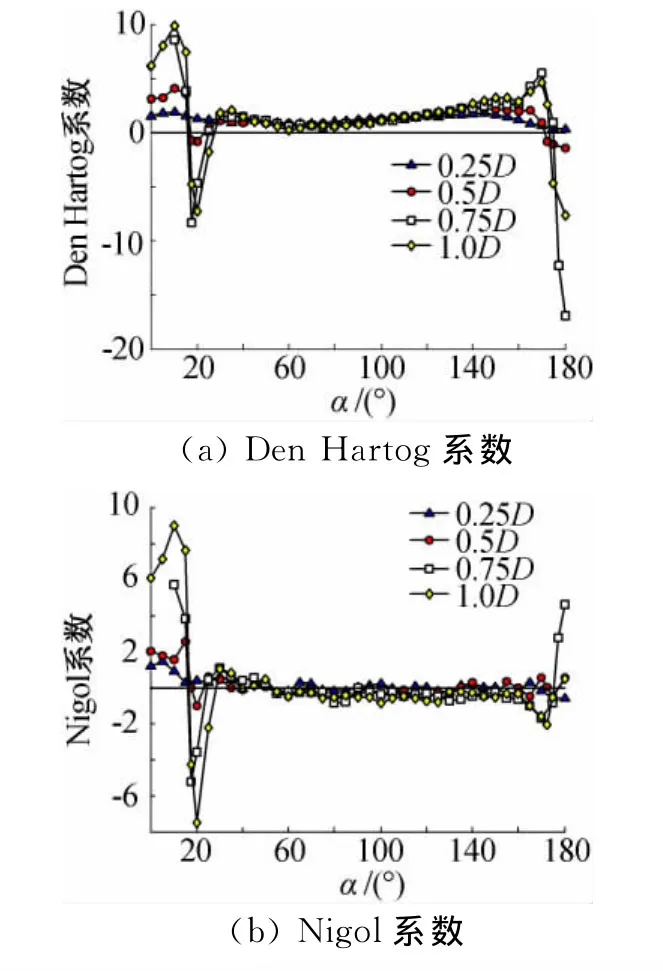
图8 覆冰单导线Den Hartog和Nigol系数Fig.8 Den Hartog and Nigol coefficients of single iced conductors

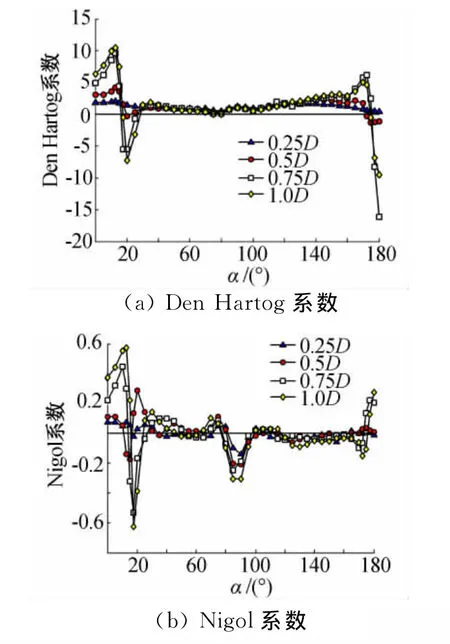
图9 二分裂覆冰导线Den Hartog和Nigol系数Fig.9 Den Hartog and Nigol coefficients of two bundle iced conductors

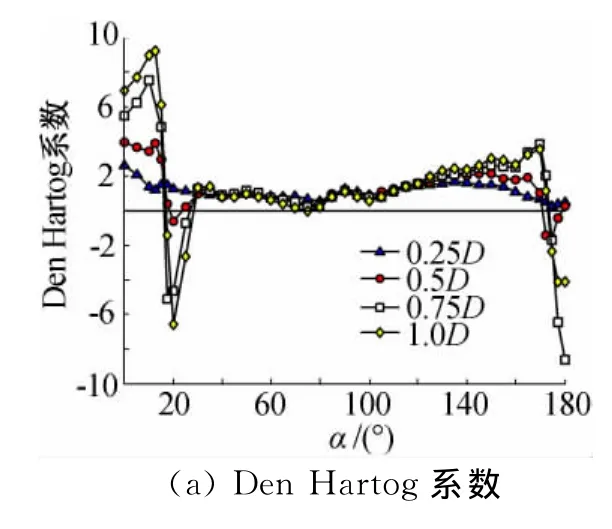
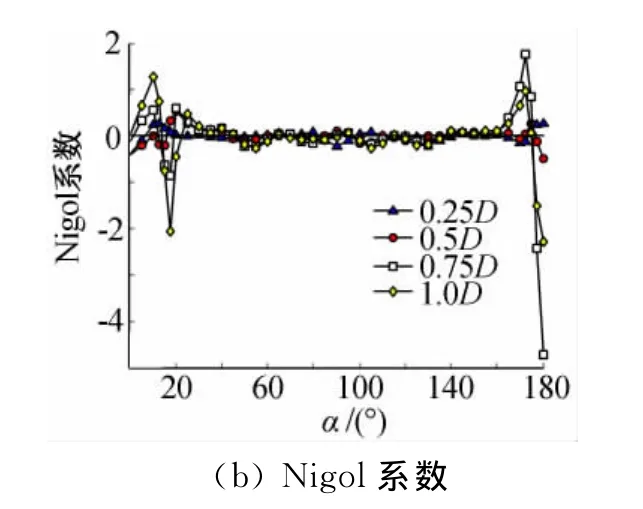
图10 四分裂覆冰导线Den Hartog和Nigol系数Fig.10 Den Hartog and Nigol coefficients of four bundle iced conductors

4 结 论

本文通过对新月形覆冰导线节段模型的气动力测试，获得了不同覆冰厚度单导线、二、四分裂覆冰导线气动三分力系数及其随攻角的变化规律，研究了分裂导线三分力系数与单导线的区别与联系，主要结论如下：

（1）随着覆冰厚度的增加，新月形覆冰导线的升力系数的尖峰不断增大，但对1D厚度的特厚覆冰来说，大攻角下升力系数的峰值却小于0.75D。

（2）新月形覆冰导线的升力和阻力系数随覆冰厚度的增加，气动力系数绝对增大，变化规律一致。当覆冰厚度较大时，扭转系数在15°～20°之间出现较大尖峰。

（3）结合Den Hartog竖向舞动机理，新月形覆冰导线可能发生舞动的攻角范围为15°～30°和170°～180°。其中15°～30°攻角范围对Nigol舞动机理而言也是不稳定区。

（4）分裂导线的升力系数与单导线基本一致，分裂导线阻力系数由于尾流的干扰，局部风攻角范围与单导线相比有较大下降。二分裂导线在90°攻角附近最大降幅约为20%；四分裂导线在45°、135°和90°附近均有下降，最大幅度分别为15%和20%。

（5）分裂导线的扭转系数由子导线自身阻力、升力、扭转系数三部分贡献组成。由于子导线之间的气动力差异，分裂导线的整体扭转系数与单导线显著不同，也不能由单导线简单的叠加得到，计算时若采用整体气动力参数，应引起注意。

［1］郭应龙，李国兴，尤传永.输电线路舞动［M］.北京：中国电力出版社，2003.

［2］CIGRE.State of the art of conductor galloping［R］.CIGRE Technical Brochure，No.322，TF B2.11.O6，2007.

［3］MCKAY G A，THOMPSON H A.Estimating the hazard of ice accretion in Canada from climatological data［J］.J.Appl.Meteor，1969，8（6）：927－935.

［4］KIKUCHI T，TANAKA K，SAITO T，et al.Measures of icing and snow accretion on transmission line［J］.JournaloftheJapaneseSocietyofSnowandIce，2006，68（5）：457－466.

［5］YUKINO T，HASE Y，MATSUDA M，et al.Experiment of snow accretion and geometrical analysis of the shape［C］／／8thInternational Workshop on Atmospheric Icing of Structures，Tokyo，1998：95－99.

［6］肖正直，晏致涛，李正良，等.八分裂输电导线结冰风洞及气动力特性试验［J］.电网技术，2009，（5）：90－94.

［7］RENAUD K，JEAN－LOUIS.Benchmark cases for galloping with results obtained from wind tunnel facilitiesvalidation of a finite element model［J］.IEEETransactionsonPowerDelivery，2000，15（1）：367－374.

［8］王昕，楼文娟，沈国辉，等.覆冰导线气动力特性风洞试验研究［J］.空气动力学报，2011，29（5）：573－579.

［9］李万平，黄河，何锃.特大覆冰导线气动力特性测试［J］.华中科技大学学报，2001，29（8）：84－86.

［10］黄河，刘建军，李万平.覆冰导线气动力特性的数值模拟［J］.工程力学，2003，（增刊）：201－204.

［11］吕翼，楼文娟，孙珍茂，等.覆冰三分裂导线气动力特性的数值模拟［J］.浙江大学学报（工学版），2010，44（1）：174－179.

［12］DENHARTOG J P.Transmission line vibration due to sleet［J］.AIEETransaction，1932，4：1074－1086.

［13］NIGOL O，BUCHAN P G.Conductor galloping 2：torsional mechanism［J］.IEEETransactionsonPower ApparatusandSystems，1981，100（2）：708－720.