大型风力机结冰过程水滴收集率三维计算
易 贤,王开春,马洪林,朱国林
(中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳 621000)
0 引 言
风力机在寒冷的气候(温度低于0℃)环境下运行时,如果遇到含有过冷水滴的气流,或者遭遇雨雪天气,在风力机表面(包括叶片、轮毂、机舱、塔架、风速风向仪等风力机所有部件表面)会发生结冰现象。结冰会改变叶片的气动外形,破坏风力机的流场特性,使风能利用系数降低,减小出力;同时,结冰还会引起额外的过载及振动,冰载荷的不平衡会增加机组部件的疲劳,轻者,使风力机停止运行,带来经济损失,重者,造成叶片损坏甚至导致整个风机倒塌,危及人们的生命财产安全。鉴于风力机结冰的危害,近年来人们越来越重视这方面的研究[1]。
风力机结冰包括沉积结冰(Precipitation Icing,主要由冻雨和湿雪引起)和过冷水滴结冰(In-Cloud Icing,主要由过冷水滴撞击在风力机表面所引起)两种形式[2],其中过冷水滴结冰是低温气象条件下常见的一种结冰形式。水滴收集率(也称水滴局部收集系数)定义为风力机某局部区域实际所收集的水量与该区域可能收集的水量最大值之比,它表征了部件表面的水滴撞击范围以及撞击区域内水量的分布。水滴收集率是结冰研究中最重要的参数之一,只有获得水滴收集率,才能进行结冰预测、探测以及防/除冰系统设计。对于过冷水滴结冰,常用的研究手段有工程估算、结冰风洞试验和数值计算。其中试验研究是早期主要采用的方法[3-4],近年来,开始陆续出现用数值计算的手段开展研究的报道[1,5-7],由于旋转条件下风力机流场的复杂性,这些计算多采用拉格朗日法计算水滴收集率,或者采用叶片的截面翼型进行二维简化计算。本文在前期发展的飞机结冰三维计算方法基础上[8-10],建立了适合于大型风力机结冰过程水滴收集率计算的三维数值方法和计算程序,并对某1.5MW级水平轴风力机的水滴收集率进行了计算,获得了不同直径水滴在风力机表面的撞击特征以及水滴收集率在叶片上的分布规律,为开展风力机结冰防护研究打下了较好基础。
1 水平轴风力机空气流场计算方法
风力机的空气绕流场是典型的包含旋转机械的流场,对于这类流场计算,有单旋转坐标系方法、多参考坐标系(Multiple Reference Frame,简称 MRF)方法[11]、滑移网格方法、动态重叠网格方法等,其中,当流场中同时存在旋转部件和非旋转部件(如转子/定子)时,MRF方法由于其鲁棒、简便、高效的特点,在工程中得到了广泛的使用,一些CFD商业软件如FLUENT、STAR-CD、CFX等,都集成了该方法。
MRF方法的基本思路为:将计算区域分为旋转区和非旋转区,在非旋转区,流动的控制方程为非旋转坐标系(如惯性坐标系)下的方程,在旋转区域,流动的控制方程为旋转坐标系下的控制方程。对不同区域的流动分别进行求解,在区域的交界面上,要求流场的参数完全一致。
本文在原有的非旋转流场计算研究的基础上,建立了计算风力机流场的MRF方法,现概述如下。
1.1 空气流场计算的控制方程
非旋转区域空气流场计算的控制方程为低速粘流的时均N-S方程,其通用形式为:
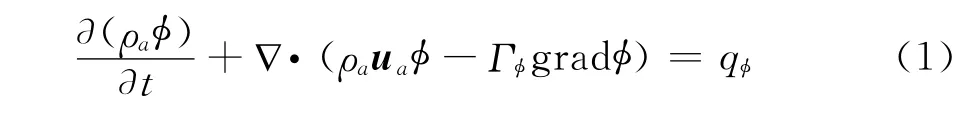
方程(1)中,φ为输运变量,ρa为空气密度,ua为空气速度,Γφ为扩散系数,qφ为源项,φ、Γφ和qφ取不同的值,可代表空气的连续性方程、动量方程和其他标量(如湍动能等)的输运方程,方程中各项的物理意义及具体表达式可参见文献[8],此处不再详述。
在旋转区域内,控制方程也可以写成输运方程的形式:
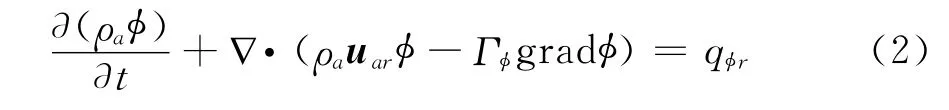
方程(2)中,uar为空气在旋转坐标系中的速度,qφr为旋转坐标系中的源项。当φ=1、qφr=0时,方程(2)为连续性方程,当φ=uar时,方程(2)为动量方程,此时源项的表达式为:
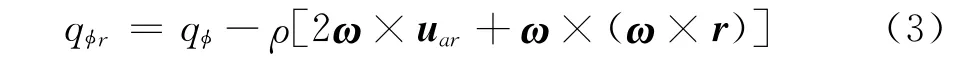
其中,ω为旋转角速度,r为流体质点在旋转坐标系中的矢径。
在旋转区域和非旋转区域的交界面上,要求流场参数一致,两个坐标系内的速度关系为:

1.2 控制方程的有限体积离散
采用有限体积法离散求解方程(1)、(2)。以点P为中心点的六面体为例,方程中各项的离散方法为:
(1)对流项的离散。
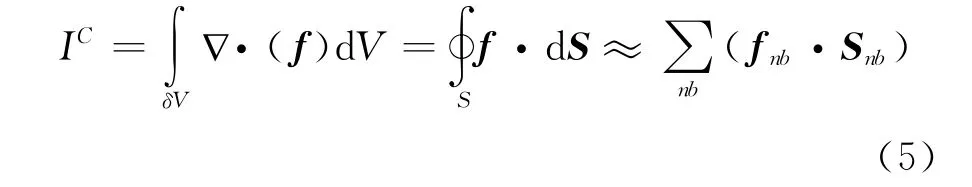
式(5)中,nb=e,w,n,s,t,b,分别代表以 P点为中心的控制体的六个面,Snb为各面对应的面积,对于空气相的控制方程有:
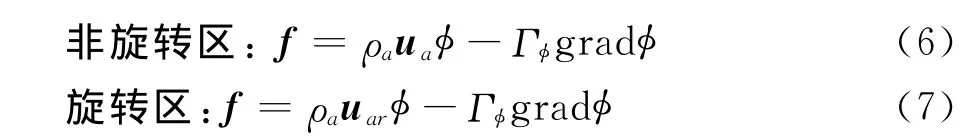
控制体界面上的变量值fnb用迎风插值和线性插值相结合的方法计算,表达式为:
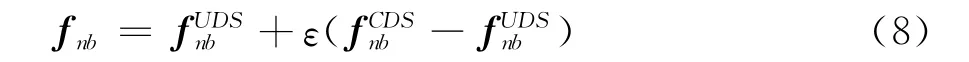
其中为迎风插值的量,为线性插值的量,ε为混合因子,0≤ε≤1。
(2)源项的离散。输运方程的源项对不同的方程都有不同的表达式,为了使其离散化表达式尽可能逼近源项本身,加强代数方程的主对角优势,提高代数方程组求解的稳定性,对源项采用线性化方式做进行处理,即令

则源项的离散形式为:
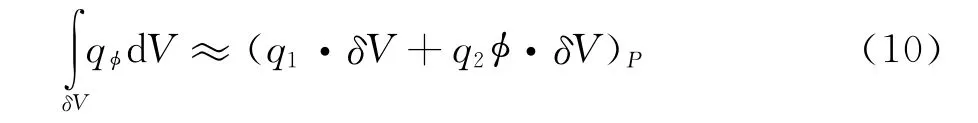
式中δV为控制体的体积。
(3)时间项离散。方程(1)、(2)的时间项采用如下二阶精度的隐式离散:
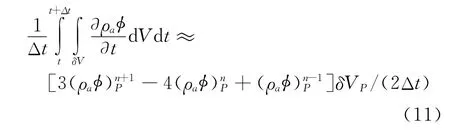
其中,上标n+1、n和n-1分别代表t+Δt时刻、t时刻和t-Δt时刻的值。
2 水滴项的控制方程及求解方法
水滴收集率计算在空气流场计算完成之后进行,主要有两种方法[12-13],一种是拉格朗日法,即用拉格朗日的观点,计算跟踪流场中单个水滴的运动,并判断其是否与物面碰撞,从而得到物面各处的水滴收集量及其分布;另一种是欧拉法,该方法将水滴看作与空气单向作用的、在空间连续分布的液态相,通过流体力学的观点求解水滴相的控制方程,得到流场中水滴容积分数分布,进而获得水滴收集率。鉴于拉格朗日法在三维计算中的不足,本文发展了三维水滴收集率计算的欧拉方法。
2.1 水滴相流场计算的控制方程
水滴相方程的求解统一在惯性坐标系中进行,引入水滴容积分数α,其定义为空间微团中水滴相所占的体积比例,则可以建立水滴相的控制方程,包括连续方程和动量方程,分别为[8]:
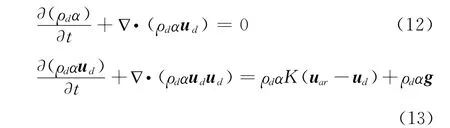
方程(12)、(13)中,ud为水滴速度,ρd为水滴密度,g为重力加速度,K为惯性因子,其表达式为:
式(14)中,μa为空气动力粘性系数,d为水滴直径,CD为水滴阻力系数,Re为相对雷诺数,其表达式为:

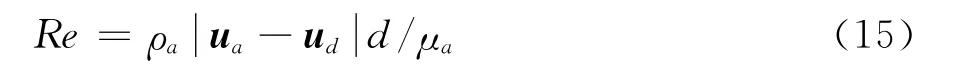
水滴运动过程中,阻力随相对雷诺数变化而变化,本文采用如下公式确定阻力[8]:
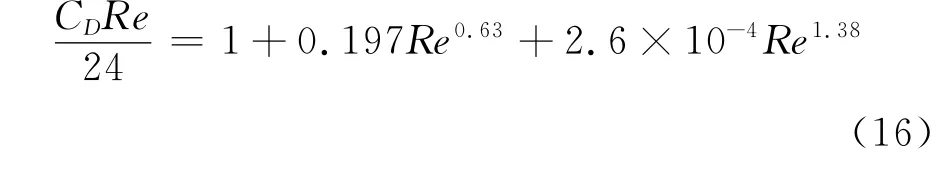
与空气控制方程类似,水滴相控制方程可以统一写成输运方程的形式:
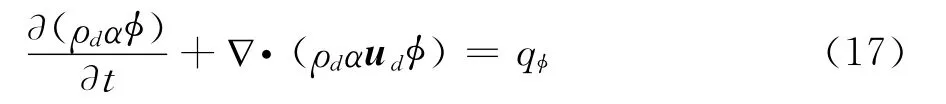
式中,qφ为源项,φ取1、ud、vd或wd分别代表连续方程和x、y、z方向的动量方程。
2.2 水滴相控制方程的离散方法
对于方程(17),对流项和源项的离散方法与方程(1)、(2)一致,时间项采用一阶显式离散,即:
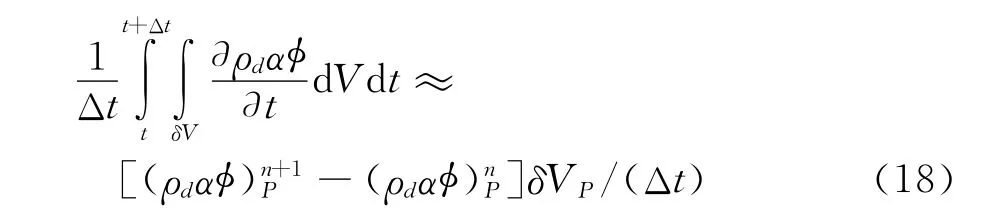
2.3 壁面边界条件
与空气流场计算在壁面采用无滑移壁面边界条件不同,对于水滴相计算,采用壁面吸入边界条件,即如果水滴与物面碰撞,则认为水滴从碰撞点流出。
3 水滴收集率的计算
由于水滴容积分数α较小(10-6量级),可以认为空气和水滴是单向作用,即只考虑空气对水滴的作用,忽略水滴对空气的作用。因此,水滴收集率的计算步骤可概括为:首先,计算空气场,本文采用SIMPLE方法计算空气场,湍流模型为标准k-ε湍流模型[14];其次,在得到空气流场分布的基础上,求解水滴相控制方程;最后,水滴收集率β可在获得当地水滴容积分数α和水滴与物面的相对速度udr之后,由以下表达式得到:

其中,α∞为远场水滴容积分数,u∞为远场来流速度,n为物面碰撞点处的单位法线向量。
由于udr=ud-ω×r,式(19)可以写成:
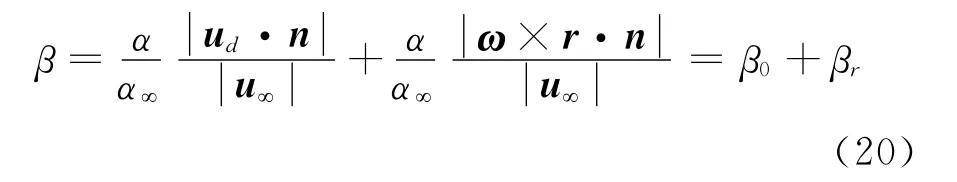
从式(20)可以看出,旋转状态下的水滴收集率β,由两部分组成,一部分是风力机旋转速度为0时的水滴收集率β0,另一部分是由于旋转而产生的水滴收集率βr。在惯性坐标系下,水滴收集率的物理意义定义为:物面某局部区域所收集的水量与该区域所收集的水量最大值之比,因此β0值应该在[0,1]区间,而βr的值则与物面某区域的旋转半径有关,半径越大,βr的值也越大。因此,在旋转条件下,由式(19)计算得到的β值将会出现大于1的情况。
4 大型风力机水滴收集率计算
根据以上数值方法,开发了相应的计算程序,并针对某1.5MW级的水平轴风力机进行了应用计算。
4.1 计算外形及网格
计算外形选用某1.5MW级的水平轴风力机,半径R=41m,忽略塔架的影响。如图1,坐标原点取为风力机轮毂中心,坐标轴方向为:x轴与远场来流方向一致,y轴垂直向上,z轴按右手系确定。计算采用多块对接网格,网格规模为1800万。图2显示了风力机表面轮毂附近的网格。
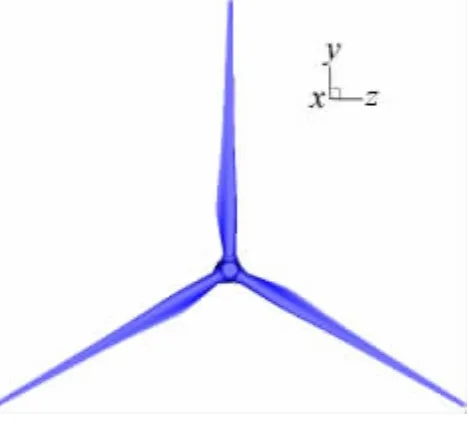
图1 计算外形及坐标方向Fig.1 Wind turbine configuration and frame
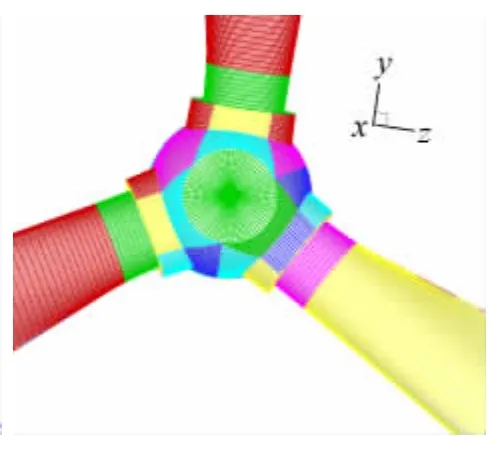
图2 轮毂附近表面网格 Fig.2 Surface grid near the hub
4.2 风力机空气流场计算结果
本文计算了两种来流条件下风力机的气动特性,并与设计值进行了对比,计算条件为:
计算条件1:来流速度8m/s,风轮转速16.7r/min,浆距角0°,叶尖速比为9。
计算条件2:来流速度11m/s,风轮转速17.4r/min,浆距角3.2°,叶尖速比为6.8。
图3给出了速度为8m/s时叶片上的压力计算结果。图3(a)给出了叶片上压力分布云图,图3(b)~图3(f)显示的是叶片上R=4m、13m、22m、31m和40m五个不同位置截面上的压力系数曲线。计算显示,在靠近轮毂附近(R=4m),由于叶片截面还不是翼型形状,迎风面和背风面的压力呈现相反的变化趋势,在30%弦长处,吸力面在迎风和背风面之间发生转换;叶片中部(R=22m)一直到叶尖附近(R=40m),压力分布呈相似的曲线轮廓。
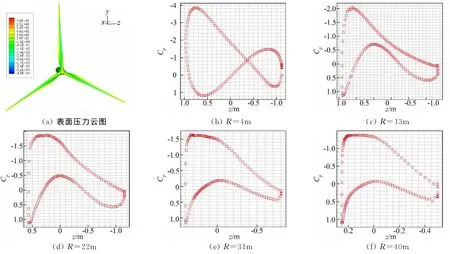
图3 叶片表面压力分布(v=8m/s)Fig.3 Pressure distribution on the blade(v=8m/s)
表1给出了两种速度条件下,本文计算的轴功率与设计值的比较,可见本文计算的功率与设计值接近,计算值比设计值只分别低0.6%和1.3%。

表1 计算的轴功率与设计值的对比Table 1 Comparison of computed power and designed power
采用固定8m/s的来流速度、改变风轮转速的方式,计算了不同叶尖速比条件下风轮的气动特性。图4(a)~图4(c)分别给出了λ=9、4和2三种叶尖速比条件下,吸力面上的极限流线分布情况。图中显示,叶尖速比λ=9时,吸力面的流动为附着流,未出现分离,整个叶片表面近似为二维弦向流动,叶尖速比λ=4时,在叶片的中部首先出现分离,当叶尖速比降至2时,整个吸力面上的流动已完全分离。
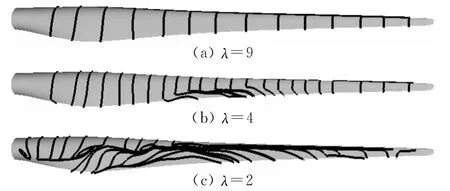
图4 吸力面极限流线分布Fig.4 Limiting streamlines distribution on suction surface
4.3 风力机水滴收集率计算结果
在风力机空气流场计算的基础上,开展了水滴收集率计算,对比了不同直径水滴的收集率在风力机表面的分布情况。计算条件为:来流速度8m/s,密度1.225kg/m3,环境压力101325Pa,风轮转速16.7r/min,浆距角0°,叶尖速比为9,水滴直径选取了三种,从大到小分别为100μm、40μm和20μm。
图5~图8给出了水滴直径d=100μm时的计算结果。图5为风力机表面的水滴收集率分布云图,由图可见,水滴主要撞击在轮毂表面和叶片前缘;图6为收集率云图在轮毂附近的放大,图7为单个叶片表面的分布云图,图8给出的是叶片表面不同展向位置的水滴收集率曲线。计算显示:(1)从叶片根部到叶尖,水滴收集率逐渐增大,叶尖附近(R=40m)的最大收集率达到7.5以上,而叶片根部附近(R=4m)的收集率仅为0.2左右;(2)轮毂上的水滴收集率极小(不到0.1),小于叶片根部的收集率。
根据以上水滴收集率计算结果,可以对轮毂表面的结冰厚度进行估算,物体表面某处结冰的厚度h可以表达为[8]:

图5 风力机表面水滴收集率分布云图(d=100μm)Fig.5 Contours of collection efficiency(d=100μm)
图6 轮毂附近的水滴收集率分布云图(d=100μm)Fig.6 Collection efficiency near hub(d=100μm)
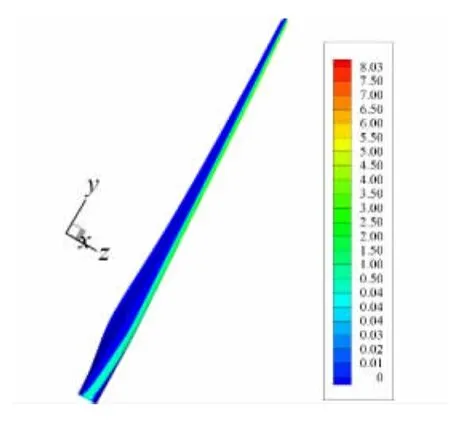
图7 叶片表面的水滴收集率分布云图(d=100μm)Fig.7 Collection efficiency on blade(d=100μm)
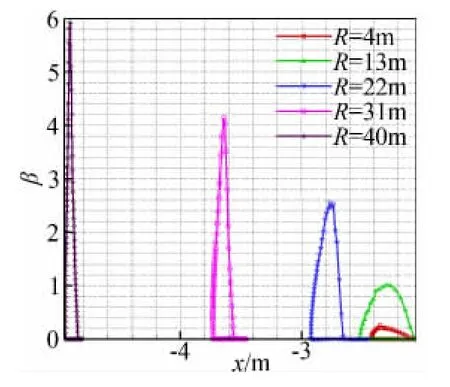
图8 叶片上不同位置水滴收集率曲线(d=100μm)Fig.8 Collection efficiency distribution on blade(d=100μm)
其中f为冻结系数(0≤f≤1),β为当地的水滴收集率,LWC为空气中的液态水含量[15],V为来流速度,dt为结冰时间,ρi为冰的密度。
根据式(20),轮毂表面β的最大值取为0.1,取f为1,V取为8m/s,LWC取0.5g/m3,ρi取700kg/m3,则1h的结冰厚度约为0.2cm,连续50h的结冰厚度也仅为10cm。由于结冰主要影响风力机的气动特性和叶片的载荷强度及疲劳特性,因此在实际分析时,可以忽略轮毂的结冰,主要考虑叶片结冰的影响。
图9、图10给出了水滴直径d=40μm时,风力机表面的水滴收集率分布;图11、图12给出的是水滴直径为20μm的结果。可以看出,水滴直径变小之后,水滴撞击特性的变化规律为:(1)水滴收集率随水滴直径变小而减小;(2)不同直径水滴在风力机表面的撞击区域以及水滴收集率在叶片上的分布特征保持类似。
图9 轮毂附近的水滴收集率分布云图(d=40μm)Fig.9 Collection efficiency near hub(d=40μm)
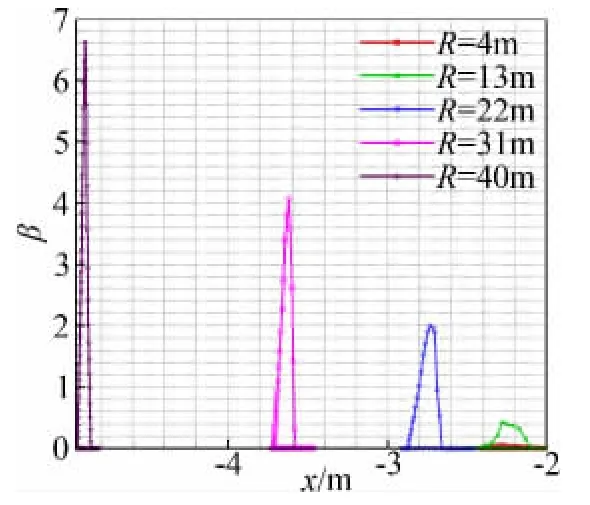
图10 叶片上不同位置水滴收集率曲线(d=40μm)Fig.10 Collection efficiency distribution on blade(d=40μm)
图11 轮毂附近的水滴收集率分布云图(d=20μm)Fig.11 Collection efficiency near hub(d=20μm)
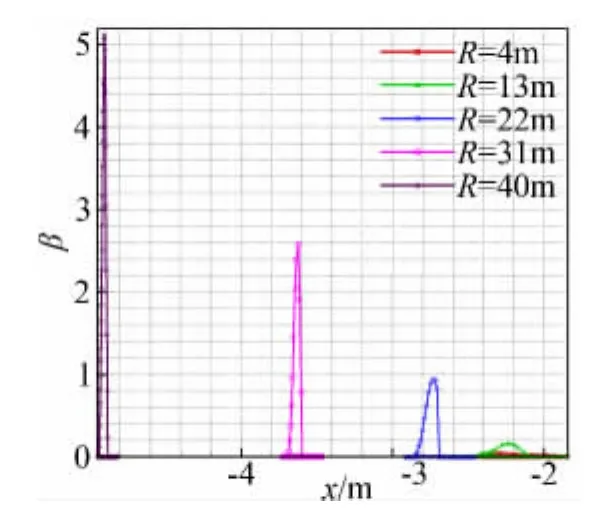
图12 叶片上不同位置水滴收集率曲线(d=20μm)Fig.12 Collection efficiency distribution on blade(d=20μm)
以上结果说明对于过冷水滴在风力机叶片表面的结冰,其基本规律有两个,一是冰主要结在叶片前缘,二是叶尖结冰远比叶根处严重。因此,在进行结冰分析、设计结冰探测方法和防除冰方案时,叶片前缘,尤其是叶尖附近的叶片前缘,需要重点关注。
5 结 论
建立了适合于大型风力机结冰过程水滴收集率计算的三维数值方法和计算程序,并对某1.5MW级水平轴风力机的水滴收集率进行了计算,得到如下结论:
(1)本文的工作基于前期发展的飞机结冰三维计算方法,旋转和非旋转区的空气流场、水滴相的控制方程均采用统一的有限体积离散方法,方便了计算程序的编制,对风力机流场和水滴收集率的计算结果初步表明本文发展的算法以及相应的计算程序是有效的。
(2)对某1.5MW级水平轴风力机结冰过程水滴收集率的计算表明,水滴主要撞击在轮毂表面和叶片前缘,轮毂上的水滴收集率极小,从叶片根部到叶尖,水滴收集率逐渐增加,且叶尖处收集率远比叶根处高。
(3)在进行结冰分析、设计结冰探测方法和防除冰方案时,可以忽略轮毂和叶片根部附近结冰的影响,叶片前缘,尤其是叶尖附近的叶片前缘,需要重点关注。
(4)风力机结冰过程涉及流动、传质、传热和相变等多种物理现象的耦合,对该问题进行三维数值模拟是一项复杂的工作,本文发展的风力机流场和水滴收集率求解方法,为进行三维结冰计算打下了较好的基础。
[1]FORTIN G ,PERRON J.Wind turbine icing and deicing[R].AIAA-2009-0274,2009
[2]FROHBOESE P,ANDERS A.Effects of icing on wind turbine fatigue loads[J].JournalofPhysics:ConferenceSeries,2007,(75):012061.
[3]JASINSKI W J,NOE S C,SELIG M S,et al.Wind turbine performance under icing conditions[R].AIAA-1997-0977,1997.
[4]HOCHART C,FORTIN G,PERRON J.Icing simulation of wind-turbine blades[R].AIAA-2007-1373,2007.
[5]MAKKONEN L,LAAKSO T,MARJANIEMI M,et al.Modeling and prevention of ice accretion on wind turbines[J].WindEngineering,2001,25(1):3-21.
[6]BATTISTI L,FEDRIZZI R,RIALTI M,et al.A model for the design of hot-air based wind turbine ice prevention system[A].Proceedings of the WREC[C].Aberdeen,2005.
[7]朱程香,王珑,孙志国,等.风力机叶片翼型的结冰数值模拟研究[J].空气动力学学报,2011,29(4):522-528.
[8]易贤,王开春,桂业伟,等.结冰面水滴收集率欧拉计算方法研究及应用[J].空气动力学学报,2010,28(5):596-601.
[9]易贤,桂业伟,朱国林.飞机三维结冰模型及其数值求解方法[J].航空学报,2010,31(11):2152-2158.
[10]易贤,桂业伟,朱国林,杜雁霞.运输机翼型结冰的计算和实验[J].航空动力学报,2011,26(4):808-813.
[11]LUO J Y,ISSA R I,GOSMAN A D.Prediction of impeller-induced flows in mixing vessels using multiple frames of reference[J].InIChemESymposiumSeries,1994,136:549-556.
[12]BRAGG M B,GREGOREK G M,SHAW R J.An analytical approach to airfoil icing[R].AIAA-81-0403,1981.
[13]BOURGAULT Y,HABASHI W G,DOMPIERRE J,et al.An eulerian approach to supercooled droplets impingement calculations[R].AIAA-97-0176,1997.
[14]ZHU G L,KRONAST M.The calculation of ground effect on a car flow field using two dimensional Navier-Stokes equations[J].ACTAAerodynamicSinica,1993,11(1):35-40.
[15]易贤.飞机积冰的数值计算与积冰试验相似准则研究[D].绵阳:中国空气动力研究与发展中心,2007.

