割补法的改进和应用
袁 武,阎 超,杨 威
(1.中国运载火箭技术研究院 空间物理重点实验室,北京 100076;2.北京航空航天大学 国家计算流体力学实验室,北京 100191)
0 引 言
重叠网格[1]方法在初始挖洞结束后,若挖洞曲面距离物面很近或是直接将物面默认为挖洞曲面,则可能导致洞边界贴近物面,使网格重叠区域庞大,同时插值区流场梯度很大,影响流场求解的效率,且降低解的精度。
人们希望能将插值区从物面附近移开,以避免插值对流场计算的不利影响,因此,出现了一些在挖洞结束后能对洞面进行优化的技术,如阵面推进技术[2]和割补法[3]等。其中,割补法建立在迭代优化思想的基础上,洞边界点离散的做推进运动,经切割和填补两个阶段改善洞面的质量,由于无需人工控制洞边界点的推进距离,因此自动化程度较高,是目前最有代表性的洞面优化技术之一。
本文对传统的割补法技术进行了研究,指出其在处理复杂网格时可靠性较差,并针对割补法的缺陷提出了改进的方法,通过数值算例对新方法进行了验证。
1 割补法简介
割补法将挖洞结束后形成的网格洞边界经切割和填补两步,逐渐推离物面,最终在远离物面的地方形成网格重叠区域。在切割阶段,由洞边界点构成的阵面逐步远离物面向外扩张,直至再也没有网格单元重叠;填补阶段,洞边界面逐步收缩,直至出现洞外网格单元(即正常点)的重叠。填补结束后,如果希望得到两层插值边界,以确保流场求解时的二阶精度,需要将邻近洞边界的洞内点转变为插值点。
割补法在优化过程中,洞边界点沿网格线离散地作推进运动,每次推进的距离就是该段网格线的长度。当网格尺度在各方向上相差较大,或网格形状匹配性差时,推进阵面在空间上参差不齐,容易有个别洞边界点异常,即产生“孤点”,严重时能导致整个推进阵面崩溃,使重叠失败。
2 割补法的研究和改进
2.1 缝隙问题和两类洞内点
在割补法的实际应用中发现[4],当物面距离很近时,填补过程容易因为少数洞边界点找点过程的失败而导致网格进入物面内。图1是前缘襟翼网格重叠失败的示例,切割结束后,主翼网格的洞边界紧挨襟翼后缘,在填补过程中,洞边界向相邻的洞内点收缩,在襟翼后缘A点处,洞边界推进物面,并迅速将襟翼内的全部洞内点转换为正常点,使重叠失败。
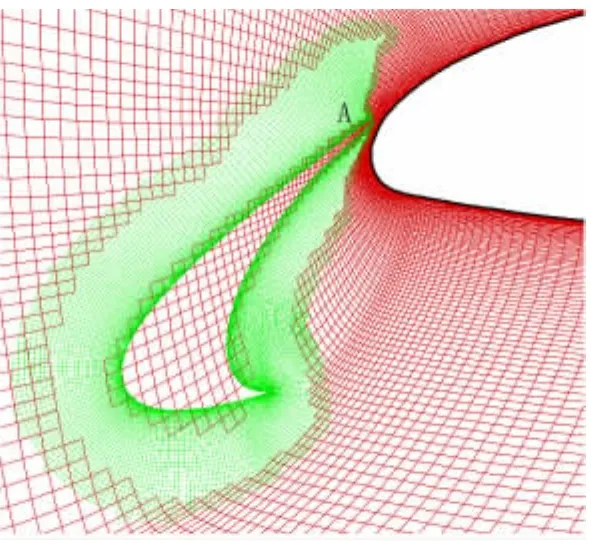
图1 前缘襟翼网格重叠失败示例Fig.1 Failure of the grid overset for the multi-element airfoil
有经验的设计人员在搭建网格时就会考虑如何避免狭缝重叠失败,例如将缝隙适当增大,或者在缝隙附近加密网格等。但人们更希望通过对重叠网格方法的改进来解决这一问题。注意到在网格区域中,洞内点可以划分为两类(参见图2)Ⅰ型洞内点是由挖洞产生的,落入物面内部的点;Ⅱ型洞内点是洞面优化中,在洞边界逐渐推离物面的过程中产生的。图1示例重叠失败的直接原因就是,落入襟翼内部的Ⅰ型洞内点在填补过程中被错误修改。
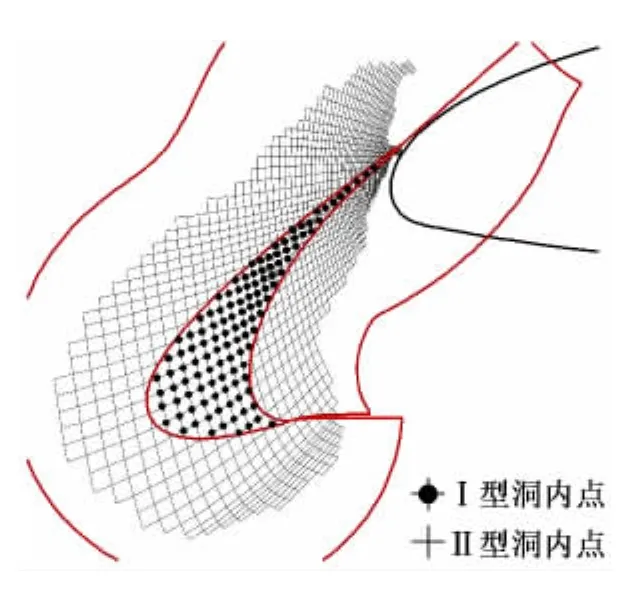
图2 两类洞内点Fig.2 Two kinds of hole point
因此,一种十分自然的思想就是在优化过程中对两类洞内点区别对待,Ⅰ型洞内点被物面屏蔽,不在流场中,洞内点属性应受“保护”不被修改;Ⅱ型洞内点是洞面向远离物面方向扩展的结果,在填补过程中,洞面收缩,Ⅱ型洞内点属性是允许修改的。因此,在程序中对两类洞内点进行区分,填补时,若相邻的洞内点为Ⅰ型洞内点,则不修改相邻点,洞边界在该处停止移动。采用新方法研究前缘襟翼重叠问题,参见图3,狭缝处挖进物面的问题得到了解决。
2.2 孤点和双阵面推进
目前,二阶空间离散格式在工程应用中较为广泛,对重叠网格,希望在重叠区域能建立两层插值边界,以满足二阶格式在重叠边界处求解精度的要求。然而在某些情况下,这一要求并不容易满足。一种常见的情况仍然是缝隙问题,图4是弹身和尾舵网格重叠示例,切割结束后,弹身网格洞边界在尾舵前缘处沿轴向向外推出了一层,就因与尾舵网格沿法向推出的洞边界相遇而停止移动,因此弹身网格在尾舵前缘处最多只能建立一层洞边界,导致局部插值精度降低。
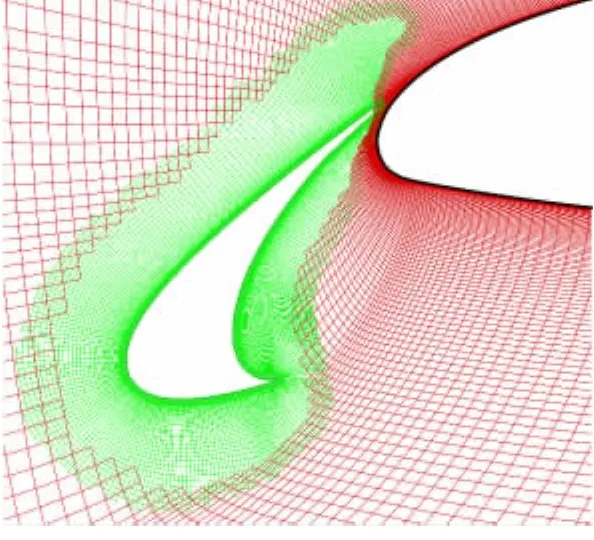
图3 前缘襟翼网格重叠示例Fig.3 Illustration of the grid overset for the multi-element airfoil

图4 弹身和尾舵网格切割结束时示意Fig.4 Illustration of cutting result for the missile body and rudder configuration
另一种情况,在填补结束后建立两层插值边界时,第二层边界上可能出现有插值点找不到有效贡献单元的问题,特别是当重叠区落在网格扭曲或长细比较大的区域时。图5是二维情况的示意,由于网格因素使洞边界参差不齐,但已建立的一层洞边界,各点均能找到有效贡献单元,满足填补过程迭代终止的条件,因此是一种可能的情况。第二层插值边界由洞边界向洞内点一侧建立,mesh1中与洞边界点A相邻的洞内点B,即默认的第二层插值点,而B点贡献单元顶点中包含对方的洞内点C,是一个无效的插值点。文献[5]称之为孤点,一些求解器中也有针对孤点的解决方案,但流场求解精度在局部的降低是不可避免的。需要注意的是,切割阶段也会产生孤点,文献[6]给出了有效的解决措施,本文主要讨论填补时的孤点问题。

图5 二维网格填补阶段结束后重叠区示意Fig.5 The overset area after the paste procedure for the two-dimensional grid
上述两种情况,前者是两物体物面距离太近,缝隙处在交叉方向上只覆盖了一层网格,理论上已经无法建立两层插值边界,只能通过增大缝隙或加密网格来改善;后者是由于洞边界落在网格扭曲或网格差异性较大区域,割补法不能正确处理,因此是本文希望解决的一种情况。
传统的割补法在优化过程中,只有一层洞边界“活动”,对默认的第二层边界即相邻的洞内点没有约束,因此优化结束时无法确保第二层边界有效。本文提出了一种在填补阶段双阵面推进的思想,即将与洞边界相邻的洞内点作为第二层洞边界,两层边界同时进行检查和推进,当两层边界均满足迭代终止的条件时,填补阶段结束,此时保留的两层边界即最终的插值边界。
双阵面推进需解决的关键问题是当第一层边界点满足要求,而第二层边界点错误时,如何驱动阵面跨过第一层边界点。方法的实现过程简述如下:
1)用切割阶段结束后产生的洞边界点和相邻的洞内点构造阵面,分别记作frg1和frg2,阵面点处于“活动”状态;
2)寻找阵面点的网格贡献单元,并依次进行以下判断:
i.若贡献单元顶点不含洞内点,该阵面点进入非活动状态;
ii.若贡献单元任一顶点是洞内点,则若该阵面点是frg1,标记为正常点;若该阵面点是frg2,标记为临时属性frg_tmp。
3)检查阵面点,进行以下判断:
i.若frg1与frg_tmp相邻,修改frg1为正常点;
ii.若frg2与正常点相邻,修改frg2为frg1。
4)再次检查阵面点,将frg_tmp修改为活动的frg1;若阵面点是frg1,将相邻的洞内点标记为活动的frg2。
5)重复上述步骤2至4,直到再也没有活动的阵面点。
方法在步骤2和步骤3中,当frg1满足要求,而frg2是无效插值点时,将frg1修改为正常点,frg2经frg_tmp再修改为frg1,成功的实现了洞边界的调整。
2.3 改进的割补法
本文在传统割补法的基础上,引入了两类洞内点的概念,和双阵面推进的思想,提出了一种改进的割补法,其思路参见图6。新方法将初始挖洞产生的洞内点,标记为Ⅰ型洞内点,并将相邻的正常点修改为初始洞边界。在切割过程中,保持一层洞边界向远离物面的方向推进,产生的洞内点标记为Ⅱ型洞内点。填补过程中,将与第一层洞边界相邻的Ⅱ型洞内点修改为第二层洞边界,两层边界同时保持“活动”状态,进行贡献单元属性的检查和判断,优化结束的条件是两层边界点同时满足有效插值点的要求,此时保留的两层边界点即为最终的插值边界。
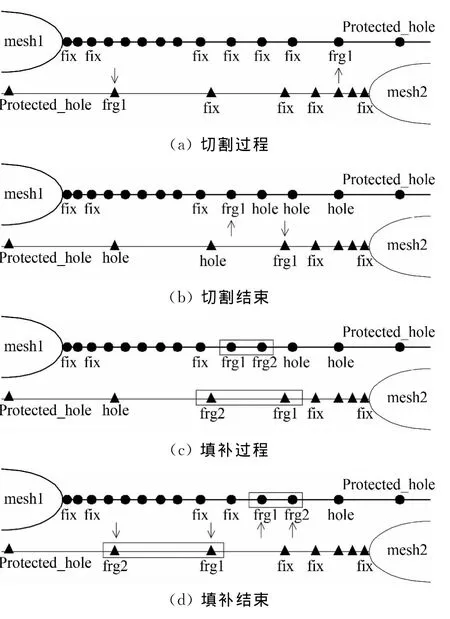
图6 改进的割补法一维示意Fig.6 One dimensional procedure for the improved cut-paste method
填补过程中,若洞边界点有相邻的Ⅰ型洞内点,认为洞边界在局部区域已推至物面附近,在此处应停止推进。有一种可能的情况是图4所示缝隙问题,此时由于两类洞内点被区分,不会出现挖进物面的问题,但局部可能无法建立两层插值边界,程序中会作一些适当的处理,以确保在以局部精度损失为代价的条件下,使重叠过程得以继续。
3 计算方法
3.1 重叠网格方法
本文改进的割补法技术已在MI-GRID中得到应用。MI-GRID是北航阎超课题组研制的重叠网格软件,核心模块采用洞映射和割补法技术,包含了孤点清除、体积优化、物面重叠、动态重叠等方法[7-8]。该重叠网格软件计算效率高、可靠性好、使用方便,先后参与了国内多个航空航天型号研制工作,包括复杂外形飞行器、子母弹抛撒、助推级分离、折叠翼打开等项目,得到了有效考核。
3.2 数值方法
本文算例均求解雷诺平均NS控制方程,空间离散采用Roe的FDS格式,MUSCL插值方法和Van Albada限制器用于获得二阶空间离散精度;湍流模型采用SST剪切应力输运模型;时间离散采用稳定性高的LU-SGS隐式计算方法。关于数值方法具体可参考文献[9]。
4 算例研究
4.1 Titan IV运载火箭
本文对美国大力神四号(TitanⅣ)大型捆绑式运载火箭的超声速绕流问题[10]进行数值模拟研究。计算条件为:M∞=1.6,ReL=1.1×107,α=0°,由于流动条件对称,故使用半模计算。采用重叠网格方法分别生成芯级和助推级的计算网格,网格数目为190万和40万。
TitanⅣ运载火箭采用并联式布局,芯级和助推级距离较近,是典型的狭缝重叠问题。图7是本文方法建立的对称面重叠网格和流场结果,芯级和助推级之间的缝隙得到了准确描述,重叠结果正确,流场结构清晰合理。图8是本文方法和传统割补法重叠结果的比较,显然传统割补法没有区分两类洞内点,在狭缝重叠时因填补中阵面点判断错误,使阵面推进物面,导致重叠失败。
图9是火箭芯级中心线上的压力分布与实验值的比较,计算结果与实验值吻合很好,说明本文改进的方法重叠结果较好。图9中,因为在风洞实验中,芯级与助推级间存在连接机构,导致实验的峰值点略高。
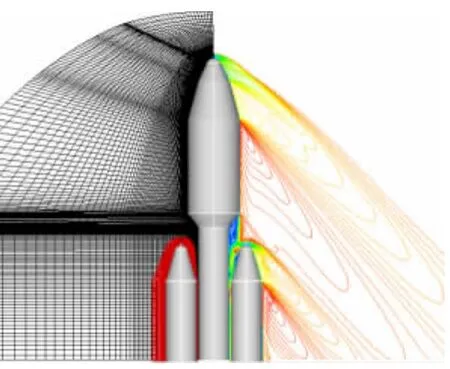
图7 对称面重叠网格和等马赫线流场图Fig.7 Illustration of the overset grid and Mach contours for the symmetry plane
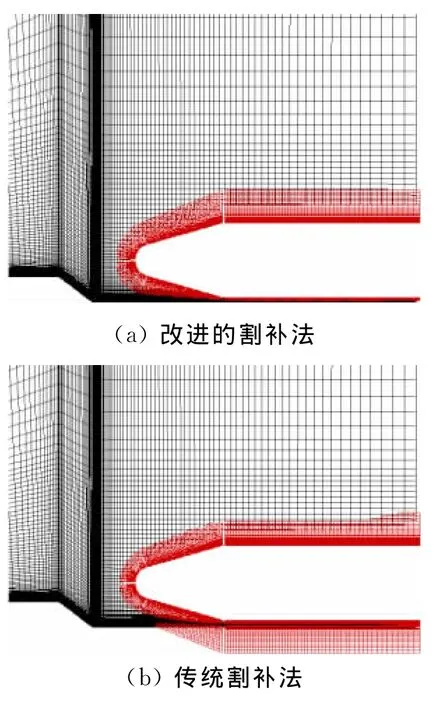
图8 不同方法重叠结果比较Fig.8 Comparison of the different overset methods
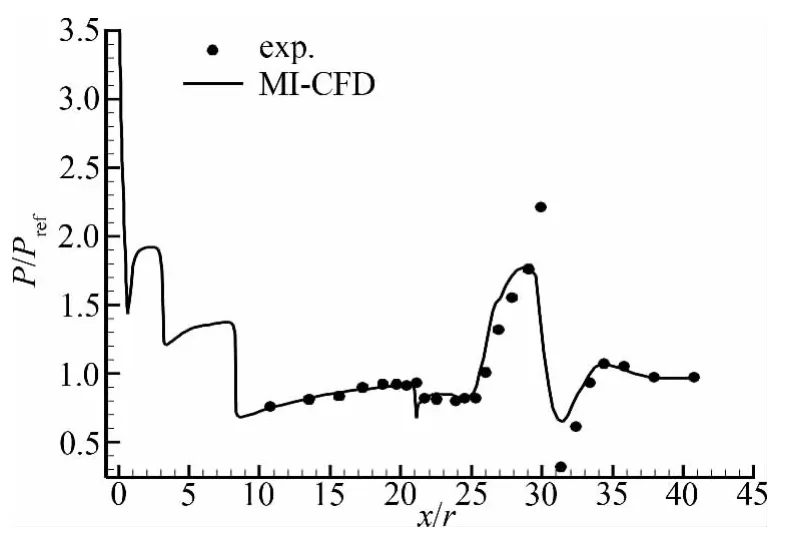
图9 芯级中心线压力分布Fig.9 Pressure distribution of the central stage
4.2 子母弹抛撒算例
子母弹抛撒的空气动力学问题是一类典型的超声速或高超声速多体干扰、非定常复杂流动问题。采用重叠网格方法求解子母弹抛撒问题,已成为国内外最常用的方法[11-12]。本文对典型外形的子母弹抛撒问题进行了研究,母弹模型包含弹仓,子弹模型包含呈十字布局的四片尾翼。计算条件为:抛撒马赫数3.0,抛撒高度10km,母弹迎角0°。母弹、子弹和四片尾翼分别生成计算网格,其中母弹网格数目为320万,子弹网格数目为42万,单个尾翼网格数目30万。
图10、图11是采用本文方法建立的子母弹模型重叠网格示意。在弹仓附近,由于网格过渡需要,母弹网格沿径向较密,使重叠区附近母弹网格各方向尺度,及母弹网格与子弹网格之间的差异较大,这对割补法一类按逻辑坐标推进的迭代优化方法是不利的,但本文方法仍能正确生成重叠网格。图12对子弹模型重叠结果的比较则更为直观,传统割补法产生的重叠区在上述不利区域容易产生孤点,而改进方法在同样情况下,在第二层边界建立失败时,能由第二层边界驱动重叠阵面继续推进,避免了孤点的产生,使重叠结果较好,重叠边界整洁。
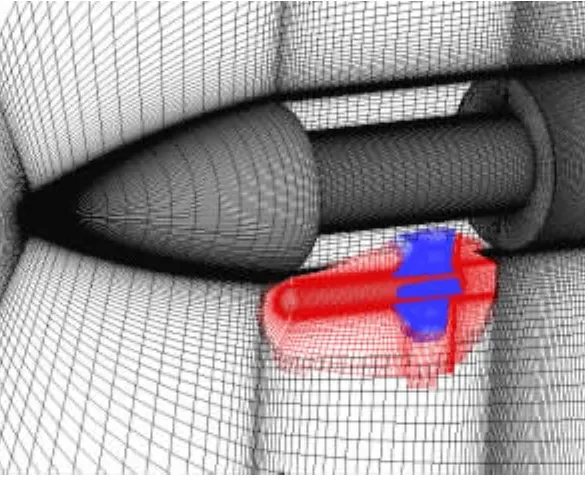
图10 对称面重叠网格示意Fig.10 Illustration of the overset grid for the symmetry plane
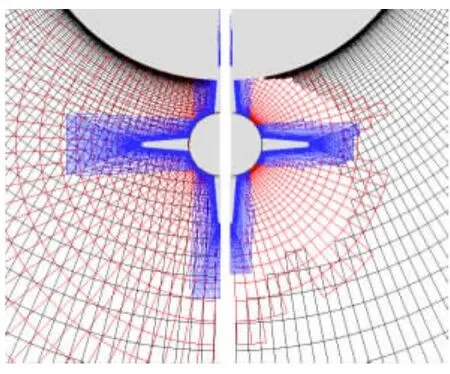
图11 截面重叠网格示意Fig.11 Illustration of the overset grid for the truncated plane
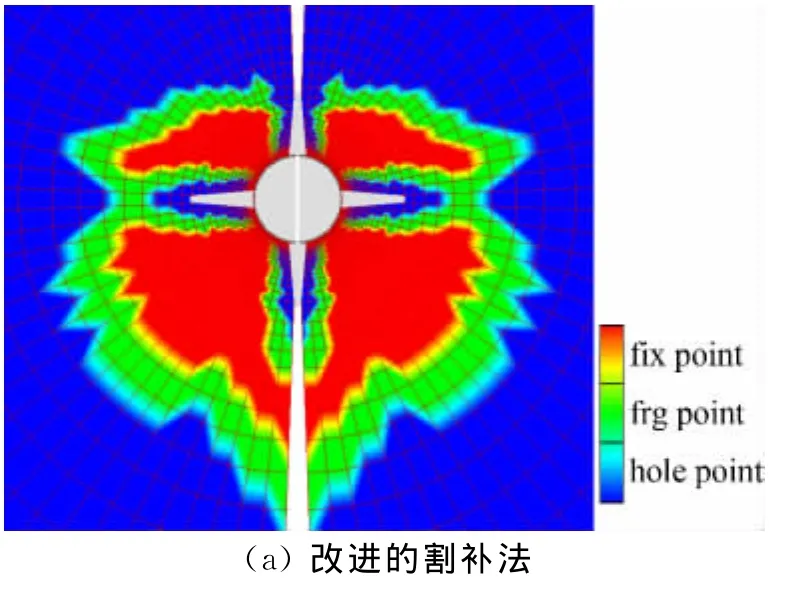
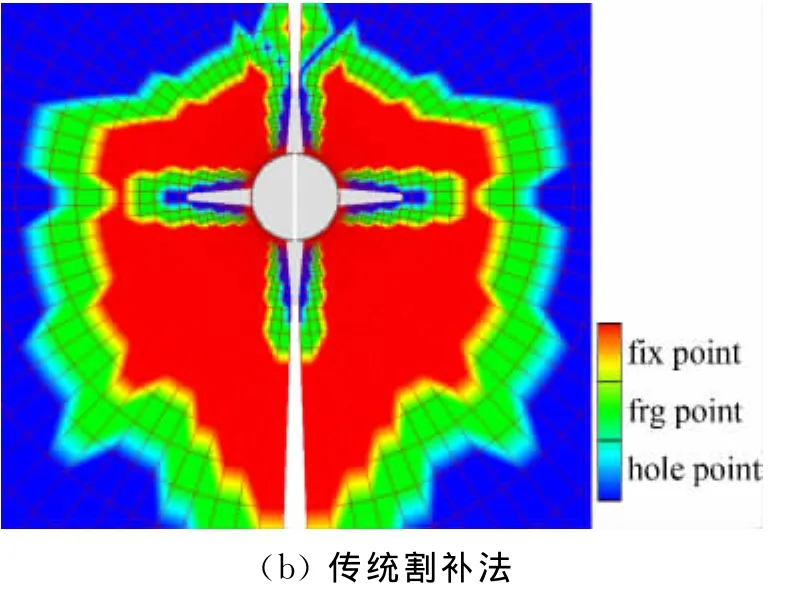
图12 子弹模型不同方法重叠结果比较Fig.12 Comparison of the different overset methods for missile configuration
图13是由数值计算获得的对称面和截面流场图,图中流场等值线在重叠区衔接较为光滑,流场结构清晰,说明本文使用的重叠网格方法和CFD求解方法对子母弹抛撒流场具有较强的解算能力。
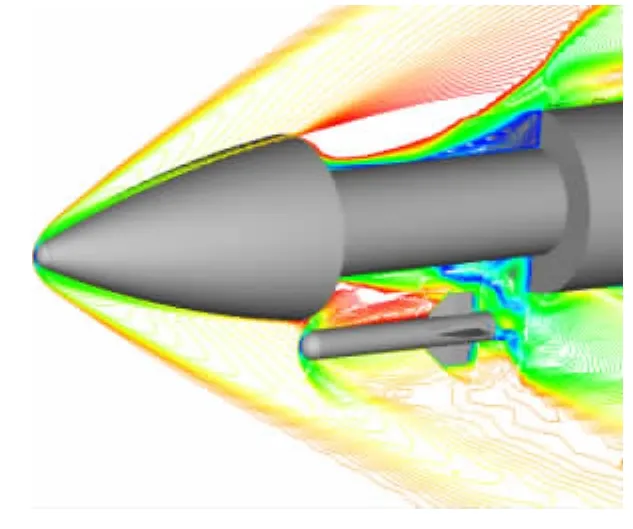
图13 对称面等马赫线流场图Fig.13 Mach contours of the symmetry plane
5 结 论
本文对割补法进行了研究,指出传统的割补法在处理缝隙、网格扭曲、网格差异性大等情况时可靠性较差,在此基础上进行了改进,主要有:
(1)提出了两类洞内点的概念,将在物理上被屏蔽的洞内点和切割过程中产生的洞内点区分,前者在填补阶段不允许修改,从根本上避免了挖进物面的问题;
(2)针对网格扭曲或网格差异大,可能无法建立两层有效插值边界的问题,提出了双阵面联动推进的思想,当第二层边界点不满足要求时,能有效驱动阵面继续推进,避免了第二层插值边界无法建立的问题;
(3)经算例研究,本文针对割补法提出的改进能有效解决狭缝重叠、网格扭曲等复杂网格情况。
[1]RALPH W N,JEFFREY P S.A summary of the 2004 overset symposium on composite grids and solution technology[R].AIAA 2005-921.
[2]WEY T C.Development of a mesh interface generator for overlapped structured grids[R].AIAA 1994-1924.
[3]CHO K W,KWON J H.Development of a fully systemized chimera methodology for steady/unsteady problems[J].JournalofAircraft,1999,36(6):973-980.
[4]FAN J J,YAN C.Enhancement and application of overset grid assembly[J].ChineseJournalofAeronautics,2010,23(6):631-638.
[5]RALPH W N,DAVID A B,ROBERT F K.Suggar++:an improved general overset grid assembly capability[R].AIAA 2009-3992.
[6]李亭鹤,阎超,李跃军.重叠网格技术中割补法的研究与改进[J].北京航空航天大学学报,2005,31(4):402-406.
[7]李亭鹤.重叠网格自动生成方法研究[D].北京航空航天大学,2004.
[8]范晶晶.复杂重叠网格方法研究及多体运动的非定常流动模拟[D].北京航空航天大学,2010.
[9]阎超.计算流体力学方法及应用[M].北京航空航天大学出版社:2006,245-248.
[10]STEPHEN T,JOHNSON C T.Launch-vehicle simulations using a concurrent,implicit Navier-Stokes solver[R].AIAA 95-0223.
[11]SPINETTI R L,JOLLY B A.Time-accurate numerical simulation of GBU-38sseparating from the B-1Baircraft with various ejector forces,store properties,and loadout configurations[R].AIAA 2008-187.
[12]张辉.重叠网格技术在飞行器多体分离问题中的应用[D].北京航空航天大学,2010.

