涡环旋转伞开伞稳定性及减速导旋运动特性研究

郭 锐，刘荣忠，胡志鹏，马晓冬

（1.南京理工大学 机械工程学院，江苏 南京 210094；2.西安交通大学 航天航空学院，陕西 西安 710049）

0 引 言

降落伞是一种应用极为广泛的柔性软质气动力减速装置，采用只能承受拉伸力，而不能承受压力和弯曲力的特殊纺织材料组成［1］。涡环旋转伞是一种常见的旋转降落伞，由于伞衣的高速旋转，使得带涡环旋转伞的物伞系统在下降时具有良好的稳定性。此外，它还具有开伞动载小、阻力系数大的优点，所以被广泛应用于兵器的弹道控制、飞机的着陆减速和控制、空降空投、航天飞行器的安全回收技术以及火星金星等外太空的探险和着陆等领域［2－3］。

在工程界和学术界，国内外众多研究者对降落伞系统进行了大量研究和探索，降落伞的设计主要基于“设计－试验－评估改进－再设计－再试验”的设计思想。在降落伞的工程应用中，需要依赖大量的风洞试验、空投试验或射击试验来判断其运动特性［4－5］。但是，已有研究多关注轴对称的平面圆形或锥形减速伞系统，研究内容也多集中在物伞系统飞行动力学［6－10］、开伞充气过程的流场特性［11－15］方面，对旋转降落伞尤其是涡环旋转伞的运动特性尚缺乏比较系统的研究。

本文以一种典型的涡环旋转伞系统为研究对象，通过伞塔投放试验方法，研究了涡环旋转伞的开伞稳定性和减速导旋运动特性，获得了伞衣幅的结构参数及伞绳的连接方式对其减速导旋运动的影响规律，从而为涡环旋转伞的结构设计和推广应用提供一定的理论依据。

1 涡环旋转伞系统减速导旋运动模型

1.1 典型涡环旋转伞系统结构特点

本文研究的涡环旋转伞系统主要由4部分组成，包括伞衣幅、伞绳、旋转接头及载物。如图1所示。

涡环旋转伞的结构复杂，它一般由4片伞衣幅和多根不同长度的伞绳连接而成，如图2所示。伞衣幅上不对称的开口设计可以实现降落伞在充满气的情况下，整个降落伞系统形成一定的凸面和倾斜度，在不对称空气动力和力矩的作用下实现旋转性能。

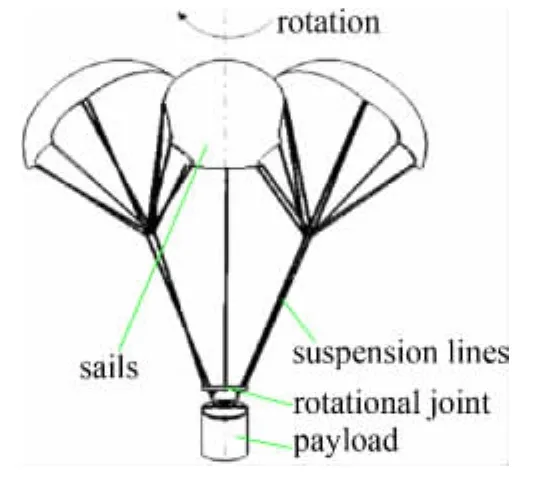
图1 涡环旋转系统结构简图Fig.1 Configuration of the vortex ring parachute－payload system

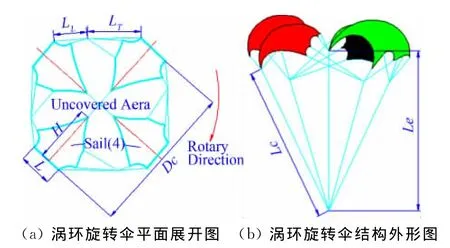
图2 涡环旋转伞主要结构示意图Fig.2 Major structural dimensions of the vortex ring parachute

开伞以后，涡环旋转伞自空中下降时，作用在四个伞衣幅上的气动力沿着与伞衣幅曲率半径相反方向的分力实现减速，沿着伞衣幅面切线方向的分力形成升力和导旋力矩，使伞旋转，并通过旋转接头机构带动物体旋转。当作用在系统上的阻力等于物伞系统的重力时，达到落速稳定；而当物伞系统的极阻尼力矩等于旋转伞的气动导旋力矩时实现转速稳定。

1.2 减速运动平衡方程

涡环旋转伞系统受到的外力包括重力、阻力和升力。为简化分析，忽略涡环旋转伞姿态的变化，即不考虑升力的影响，则当物伞系统达到落速平衡状态时，物伞系统的阻力与重力相互平衡。由此有平衡方程：

式中，ρ为空气密度；g为重力加速度；md为载物的质量；mp为涡环旋转伞的质量；vbalance为系统的平衡落速；（CpSp＋CdSd）为系统的阻力特征，其中Cp为涡环旋转的阻力系数，Cd为载物的阻力系数，Sp为涡环旋转伞的迎风阻力面积，Sd为载物的迎风阻力面积。

由上式不难看出，当载物的质量一定时，涡环旋转伞系统的平衡落速与其阻力特征成反比。若不考虑伞衣幅变化带来的阻力系数微小变化，则随着涡环旋转伞面积的增加，系统的平衡落速将会降低。

1.3 转动平衡方程

涡环旋转伞受到的力矩包括气动导旋力矩、极阻尼力矩、赤道阻尼力矩及载物通过接头传递的摩擦力矩。为简化分析，忽略涡环旋转伞姿态的变化，把四个伞衣构成的涡环旋转伞视为一个整体，同时近似认为物伞系统绕图示中心轴旋转，则根据动量矩定理，涡环旋转伞的转动方程为：

式中，Jx为涡环旋转伞的极转动惯量；Mpz为涡环旋转伞的气动导旋力矩；Mxz为涡环旋转伞的极阻尼力矩。

式中，q为动压，表示单位体积中气体质量的动能，q＝ρv2；lp为伞衣特征长度，dp为伞的特征直径；为极阻尼力矩系数导数；mpz为伞的导旋力矩系数。当稳定落速不超过60m／s时，m＇xz、mpz近似为常数。

由此可见，对于结构已经确定的涡环旋转伞系统，当物伞系统的稳定落速不超过60m／s时：（1）其转速落速比k为定值；（2）由于qSplpdPm＇xz是常数，则提高转速与落速比的关键是提高涡环旋转伞的导旋力矩Mpz。

2 伞塔试验研究

2.1 涡环旋转伞模型设计

本文研究的涡环旋转伞系统由4片相同的非对称伞衣幅和34根不同长度的伞绳连接而成。考虑到载物稳定平台要求（平衡落速10m／s～15m／s，平衡转速2.5rev／s～4rev／s），因此研究时，设计了四种伞衣幅结构（P1、P2、P3和P4），并选取两种伞绳连接方式（JA和JB），其结构参数分别如表1和表2所示。其中，H表示伞衣幅高度，L表示伞衣幅长度，S表示伞衣幅面积，Dc表示伞衣幅展开的等效直径，如图2（a）所示；Lc表示中心绳长度，Le表示边绳长度，ΔL表示前后伞绳长度差。为了比较分析，选取组合后的涡环旋转伞结构方案共八种，分别是P1JA、P1JB、P2JA、P2JB、P3JA、P3JB、P4JA、P4JB。

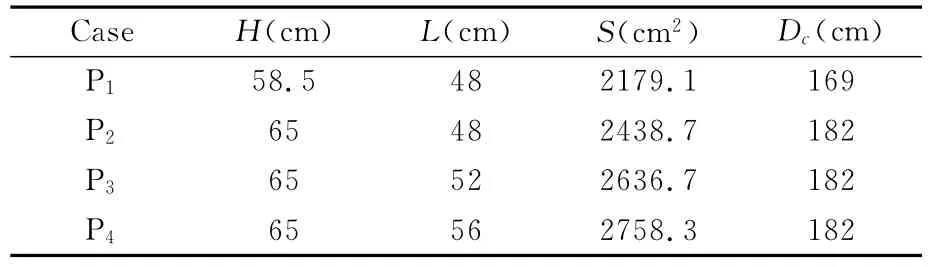
表1 伞衣幅结构参数Table 1 Configuration parameters of the parachute sail

表2 伞绳连接方式结构参数Table 2 Joint parameters of the parachute cords

2.2 伞塔投放试验方法

本文设计了一种伞塔投放试验方法，如图3所示。试验的主要目的是考察涡环旋转伞实现减速导旋性能的能力，通过改变涡环旋转伞的结构参数，研究其对物伞系统运动规律的影响程度，进而指导该类降落伞系统的总体设计。

图3 伞塔投放试验布置Fig.3 Parachute tower test

试验在湖北襄樊航宇救生设备610所进行，采用125m高的伞塔进行投放试验。将物伞系统从塔顶投下，观察其开伞程序、开伞稳定性，并通过姿态参数存储测量仪和正交布置的高速摄像仪测试并记录其下降过程中的空中姿态参数变化规律，包括滞空时间、下落速度和转动速度。

2.3 试验数据测试方法

如图3所示，基于交汇摄影测量法，采用两台高速摄像仪，使其视轴交汇于目标区，测出下降过程中的目标仰角及方位角，则可以通过三角形正弦定理计算出目标的姿态参数。本文主要关注其下降过程中的落速变化。

此外，基于地磁场的近地不变性，我们设计了一种姿态参数存储测量装置。采用三轴加速度计和三轴磁阻传感器，获得6路的加速度分量和地磁分量。试验结束回收测量仪，基于MATLAB调用存储数据进行数据处理，可以得到物伞系统在下降过程的转速变化。

3 试验结果及分析

3.1 试验结果

我们共进行了27组试验，记录了涡环旋转伞系统的自由下降过程及落地姿态，如图4所示。

因人为操作原因，高速摄像获取的完整落速数据较少，我们从试验结果中提取了8组有效试验数据，对试验采集的原始数据进行处理，得到了涡环旋转伞系统在下降过程中的落速和转速，如表3所示，部分结构方案处理后的结果如图5所示。

图4 物伞系统自由下降过程姿态Fig.4 Attitude of the parachute－payload system

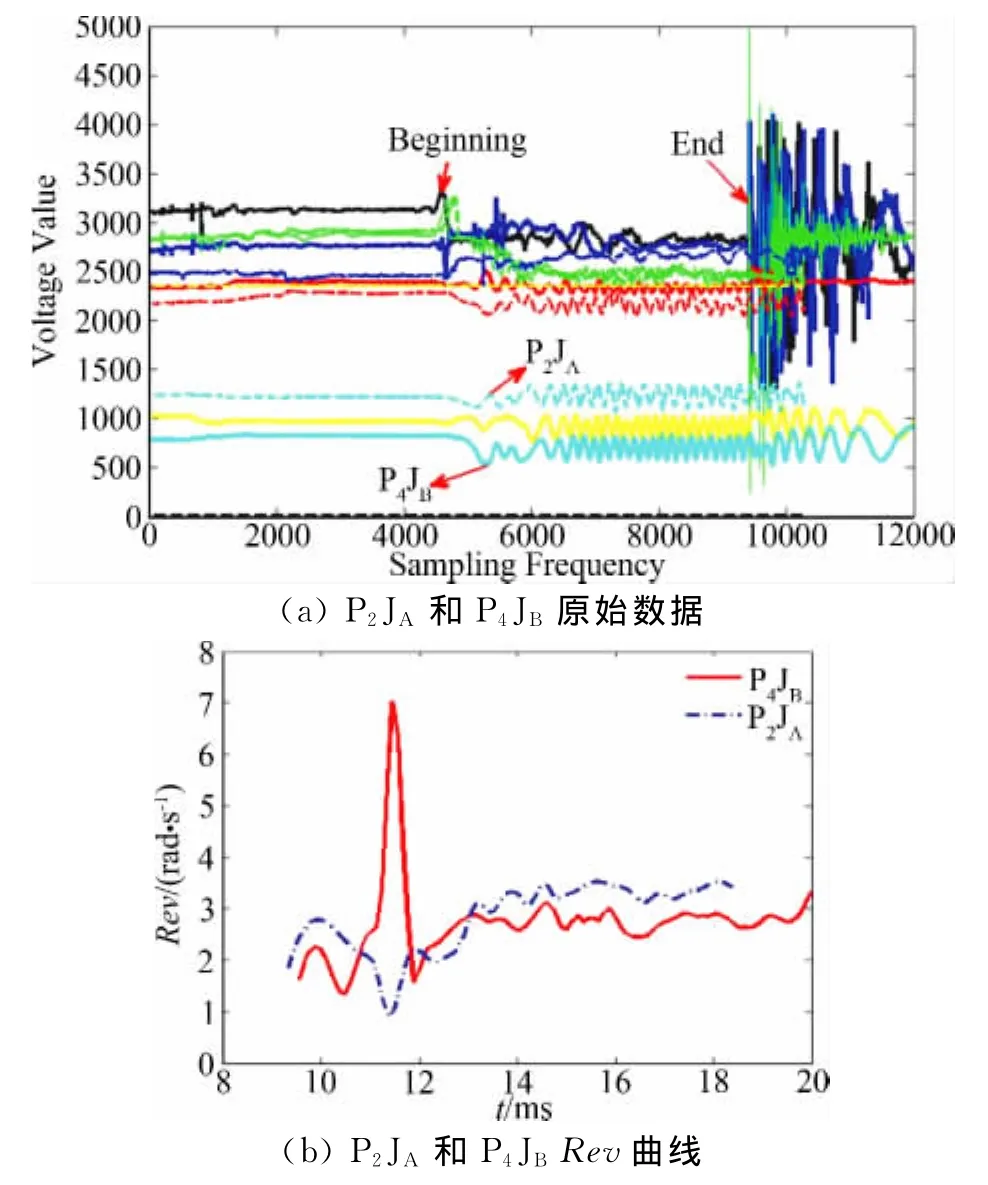
图5 部分方案的原始数据及计算得到的转速曲线Fig.5 Initial three－axial data and its calculated rotating speed of the parachute－payload system

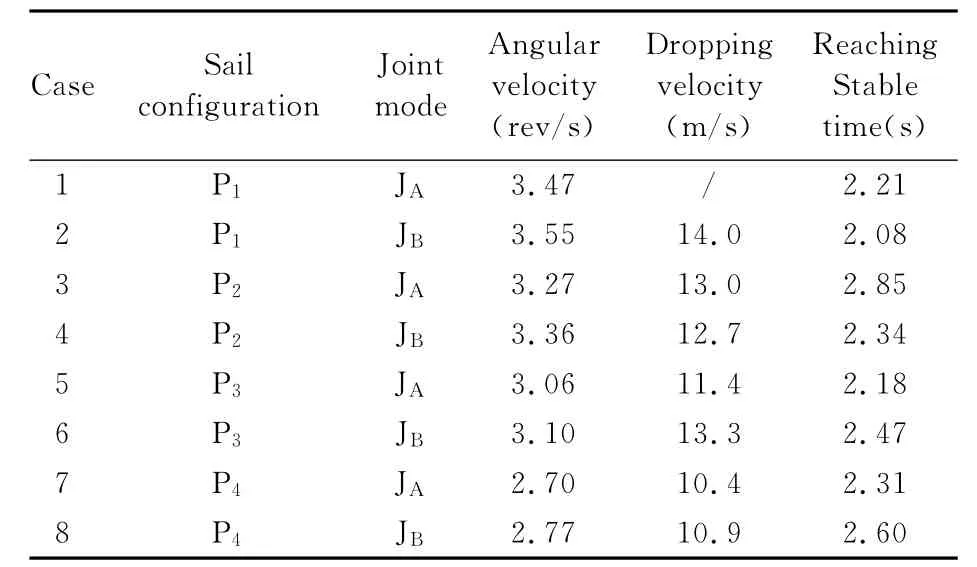
表3 伞塔投放试验数据的处理结果Table 3 Experimental results in the tower test

3.2 开伞稳定性

由表3可以看出，8种方案均顺利开伞，涡环旋转伞的伞衣在开伞充气后很快可以达到平衡转动状态，过渡时间在2～3s。当涡环旋转伞系统达到平衡状态时，物伞系统运动较为平稳，摆动较小，充分验证了涡环旋转伞的开伞稳定性良好。

由图6还可以看出，随着伞衣面积的增大，JB涡环旋转伞方案的开伞稳定时间也随之呈线性增加，这主要是由于伞衣面积增加导致的平衡落速的下降，从而影响了涡环旋转伞到达稳定的时间。从试验结果整体可以看出，JA涡环旋转伞方案的开伞稳定性波动较大，一定程度上说明JA方案的伞衣幅结构与伞绳连接方式匹配性较差，故JB方案较JA方案的稳定性好。

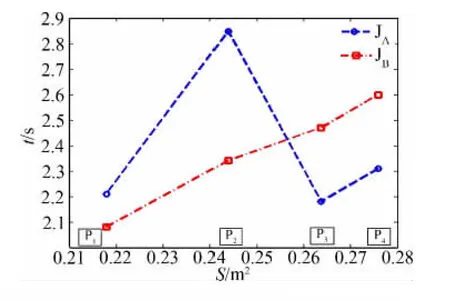
图6 稳定时间随伞衣面积的变化曲线Fig.6 Inflated stable time along with the variety of parachute area

3.3 运动特性的影响规律

由图7可以看出，当载物的质量一定，伞衣面积越大，其对应的平衡转速越低。P1结构方案的平衡转速可以达到（3.47～3.55）rev／s，而P4结构方案的仅有（2.70～2.77）rev／s。当伞绳连接方式相同时，即比较方案P1JB和P4JB的平衡转速平均值，P1方案的平衡转速比P2方案高28.16%。一般认为，伞衣面积越大，伞受到的空气导转力矩越大，所以物伞系统的转速应该越高，但试验结果与此恰好相反。实际上，这并不矛盾，由表3可以看出，平衡转速较高的方案，物伞系统的平衡落速也相对较高，这说明伞衣面积减小，伞受到阻力变小，导致其平衡落速较高，由式（3）可知，系统的平衡落速与平衡转速的比值为定值，故伞的平衡转速也较高。

由图7还可以看出，当载物的质量一定，对于同样大小伞衣面积的结构方案，方案JB的连接方式得到的平衡转速明显高于方案JA，平均值高约2.24%。比较方案P2JA与P2JB可以发现，随着ΔL增加1／3，物伞系统的转速增加2.75%，转速提高的效果较为明显。由此可知，前后伞绳差对于提高涡环旋转伞系统的平衡转速具有明显效果。

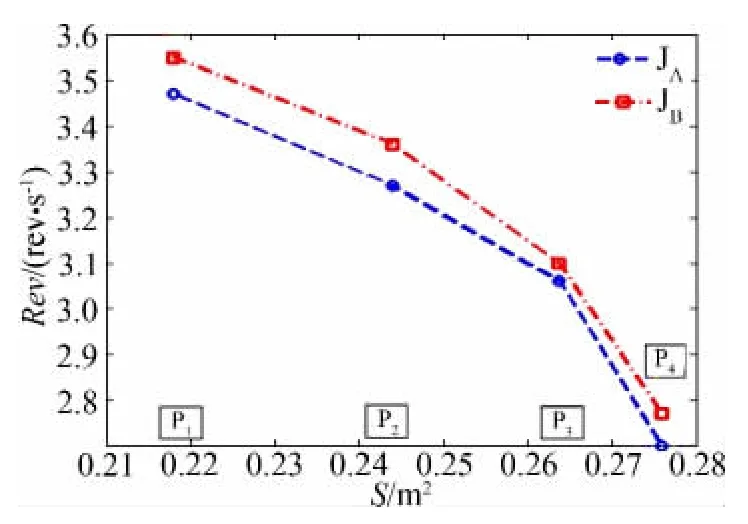
图7 平衡转速随伞衣面积的变化曲线Fig.7 Rotating angular velocity along with the variety of parachute area

图8 平衡落速随伞衣面积的变化曲线Fig.8 Dropping velocity along with the variety of parachute area

由图8可以看出，当载物的质量一定，伞衣面积越大，其对应的平衡落速越低，这与式（1）的分析结果对应一致。P1结构方案的平衡落速可以达到14m／s，而P4结构方案的平均平衡落速仅有10.65m／s。同样可以看出，当载物的质量一定，对于同样大小伞衣面积的结构方案，若剔除Case6方案的试验值（Case6方案平衡落速较高可能是由于人为或环境因素造成），则JA的连接方式得到的平衡落速与方案JB的差别不大，这主要是因为两种连接方式的伞衣平面展开直径Dc相同（如表1所示），这样，伞衣充气后得到的伞衣展开面积几乎一致，则根据式（1）可知，其平衡落速相差不大。

由前面的讨论还可以发现，当载物质量一定，随着伞衣面积的增加，系统的平衡落速和转速相应的减小，但其比值k几乎不变。如表4所示。也就是说，当涡环旋转伞系统达到平衡下降状态时，物伞系统的平衡转速和落速比是定值。在涡环旋转伞的设计应用中，通常希望涡环旋转伞在很小的速度下就能达到较高的转速。因此，在涡环旋转伞结构已定的前提下，如何提高其转速与落速之比是下一步研究的关键。

表4 平衡转速与落速比值Table 4 Ratio of the angular velocity and the balanceable dropping velocity

4 结 论

（1）在稳定落速不超过60m／s时，涡环旋转伞系统的平衡转速和平衡落速的比值约为定值。

（2）当涡环旋转伞系统达到稳定平衡状态，即落速一定、转速一定，则提高转速与落速比的关键是提高涡环旋转伞的导旋力矩。

（3）当载物的质量一定，伞衣面积越小，其转速越高。但是，随着伞衣面积的增加，系统的平衡落速和转速相应的减小。

（4）当载物的质量一定，对于同样大小伞衣面积的结构方案，前后伞绳差的增大可以提高物伞系统的平衡转速。

致谢：感谢湖北襄樊航宇救生设备610所韩晋阳及国营第5013厂胡晓东等为本文提供试验准备、样品加工及高速摄影测试工作的帮助。

［1］王利荣.降落伞理论与应用［M］.北京：宇航出版社，1997.

［2］EWING E G，BIXBU H W，KNACKE T W.Recovery systems design guide［R］.ADA 070251，1978.

［3］GUO R，LIU R Z.Dynamics model of the rigid and flexible coupling system for terminal－sensitive submunition［J］.JournalofChinaOrdnance，2007，28（1）：10－14.

［4］杨党国，范召林，李建强，等.弹舱流动特性数值模拟及风洞试验研究［J］.空气动力学学报，2009，27（3）：377－381.

［5］余莉，明晓.降落伞技术的研究进展及展望［J］.世界科技研究与发展，2005，27（5）：21－25.

［6］WATTS G.Technique to eliminate computational instability in multibody simulations employing the lagrange multiplier［R］.NASA TP 3220，1992.

［7］DJERASSI S，VIDERMAN Z.Motion analysis of two cable－connected bodies in atmospheric free－fall［J］.JournalofAircraft，1998，35（1）：78－83.

［8］MARTINS S.Modeling of parachute dynamics in a synthetic flight mechanics simulations′environment［R］.AIAA 2009－2943.

［9］JOHN D F，ROBERT H T.Multibody parachute flight simulations using singular perturbation theory［R］.AIAA 2009－2920.

［10］吴卓，曹义华，宋乾福.锥形降落伞开伞过程流动结构相互作用的数值模拟［J］.航空动力学报，2009，24（7）：1584－1593.

［11］JOHARI H.Aerodynamics of parachute opening［R］.ADA411095，Worcester，USA：Mechanical Engineering Department Worcester Polytechnic Institute，2002.

［12］JOHN A C，AMANDA M V，ROBERT D B.Statistical reconstruction of mars entry，descent，and landing trajectories and atmospheric profiles［R］.AIAA 2007－6192.

［13］VLADIMIR S D.Axisymmetric parachute shape study［R］.AIAA 2009－2944.

［14］彭勇，程文科，宋旭民，等.降落伞充气过程研究方法综述［J］.中国空间科学技术，2004，24（3）：38－44.

［15］丁娣，程文科.大型伞绳帆和抽打现象连续模型及验证［J］.航天返回与遥感，2010，31（5）：22－26.