基于变可信度代理模型的气动优化
黄礼铿,高正红,张德虎
(西北工业大学 翼型叶栅空气动力学国家重点试验室,陕西 西安 710072)
0 引 言
随着飞行器性能要求的不断提高,气动外形设计面临更大的挑战,出现了越来越多的高可信度气动分析方法。高可信度方法通常需要很大的计算量,虽然在过去的几十年间计算能力发生了巨大的变化,但高可信度模型仍然无法直接应用于优化设计。为了提高优化过程的效率,一种有效的方法是构造基于代理模型的优化方法[1-2]。
代理模型方法最基本的思路是通过构建目标函数的近似模型即代理模型,替代优化设计中复杂的气动特性分析方法,从而减少优化问题求解的计算量。目前可行的代理模型技术包括数据拟合模型、降阶模型、以及启发式模型,数据拟合模型,通常通过对高可信度模型的样本数据进行拟合或者退化得到高可信度模型输入与输出之间的关系,构造简化的近似模型,常用的方法有BP神经网络(Backpropogation Neural Net,BPNN)[3]、径向基函数(Radial Basis Function,RBF)[4]、Kriging 模型[5]、高斯过程(Gaussian Process,GP)[6]、多项式响应面(Polynomial Response Surface Method,PRSM)[7]等等;降阶模型,降阶模型的构建依赖于控制方程信息,通常由偏微分方程或者常微分方程描述的系统可以构建降阶模型,降阶模型不适合于控制方程未知或基于经验关系的情形,如使用正规正交分解(Proper Orthogonal Decomposition,POD)[8]和模型分析一类的方法得到的降阶模型;启发式模型,也被称为多可信度、变可信度、变复杂度模型,变可信度模型利用两个不同可信度的计算工具对相同的物理过程进行数值模拟,一般高可信度的方法精度较高,但需要更大的计算代价,低可信度的方法精度较低,但是需要的计算代价很低,利用大量低可信度数据来提高少量高可信度数据构造的代理模型精度,减少得到合理精度代理模型所需要的计算代价[9]。
对于复杂的多设计变量气动外形优化问题,构造精确的代理模型需要大量的样本计算量。如何在确保预测精度的前提下,降低代理模型样本计算量是代理模型研究的重要方向。变可信度代理模型因引入两种不同可信度目标函数计算模型的样本,通过利用计算量较少的低可信度模型样本,减少计算量较大的高可信度样本的计算,得到了广泛的关注[10]。本文采用Co-Kriging方法[11-12]开展变可信度代理模型研究,传统的变可信度代理模型简单的使用不同可信度模型的差值或比值实现,但是Co-Kriging方法使用两组独立的样本数据,能够处理更为复杂的关系,因此用其构建代理模型具有更大的灵活性,并且可以提供预测结果的误差估计,给样本补充提供了依据。文中通过典型函数问题研究了如何通过选样方案设计,构造高效的变可信度代理模型。在此基础上,针对RAE2822翼型气动设计问题,基于不同代理模型的翼型优化设计对比证实了该方法的工程实用性。
1 Co-Kriging变可信度代理模型
代理模型可以使用有限数量的数值模拟结果来代表真实模型。为了使用有限数量的样本数据得到高精度的高可信度模型近似,为了提高代理模型的计算效率和预测精度,人们对代理模型方法的结构和学习方法进行了大量研究,但是代理模型的预测精度与样本数量直接相关,高精度气动特性分析样本的计算代价是制约代理模型精度提高的主要因素。变可信度代理模型可以利用大量低可信度模型信息来提高少量高可信度模型数据构造的代理模型的精度,在大大减少计算量的情况下得到较高的代理模型预测精度。传统的变可信度代理模型方法利用高低可信度模型之间的差值,利用代理模型方法对高低精度模型的差值进行建模,用差值代理模型对低可信度模型的误差进行修正,提高其预测精度。由于对同一样本需分别采用高、低可信度模型进行分析,并且在使用中需要计算低可信度模型,其计算量仍然较大,而且其预测精度很大程度上依赖于低可信度模型的分析精度。Co-Kriging方法利用两组独立的高、低可信度样本数据,充分利用样本数据挖掘低可信度模型信息,降低了样本数据和代理模型使用中的计算代价。Co-Kriging方法是Kriging方法的扩展,以使用于双层甚至是多层模型的代理模型构造,其构造的代理模型的近似估计可以表示如下:
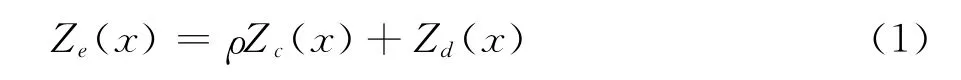
其中Zc()代表对低可信度样本数据构造的Kriging代理模型,Zd()表示对高、低可信度样本数据差值构造的Kriging代理模型。考虑两组独立的高、低可信度数据,高可信度数据有ne个样本Xe,低可信度模型有nc个样本Xc,样本点之间的协方差可以表示为:
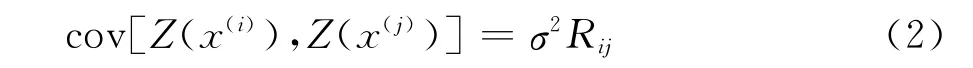
其中样本之间的相关性矩阵R是由一个空间相关函数(Spatial Correlation Function,SCF)决定的:
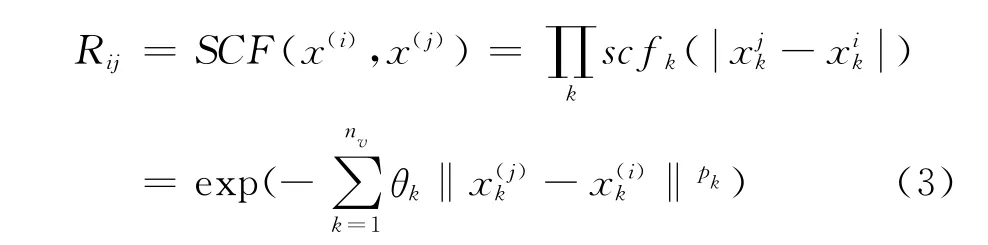
若Rc(Xc,Xe)表示样本数据Xc与Xe之间的空间相关性矩阵,则Co-Kriging方法的协方差矩阵即可表示为
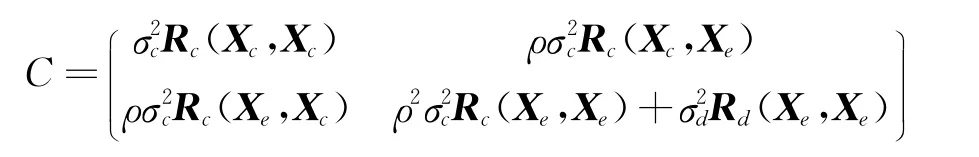
因此Co-Kriging方法有两种不同的空间相关函数,有更多的相关参数(θc、θd、pc、pd以及放大因子ρ)需要估计。由于低可信度模型数据与高可信度模型数据相互独立,相关参数θc、pc的估计求解与标准Kriging方法的求解方法相同。为了估计θd、pd以及ρ,首先定义:

其中yc(Xe)是在点Xe处低可信度模型的值yc。这样就可以采用与标准Kriging类似的优化过程来求得对θd、pd以及ρ的估计。Co-Kriging模型的预测估计式可表达如下:
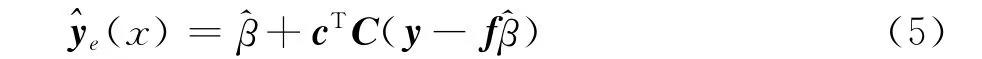
其中=(fTC-1f)-1fTC-1y,f表示值全为1的ns维列向量
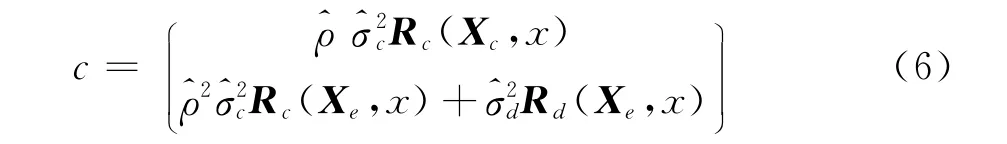
同Kriging方法一样,Co-Kriging方法也可以给出估计值的均方误差估计,其表达式为:
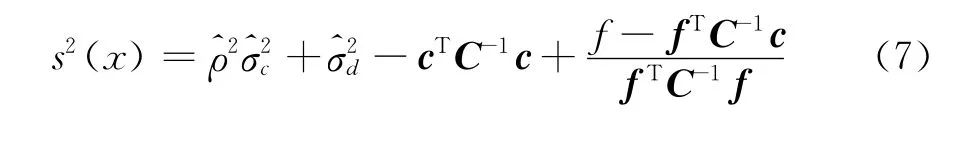
2 选样方案研究
代理模型的近似精度与样本数量和样本可信度直接相关,Co-Kriging变可信度代理模型可以使用两组独立的高、低可信度样本数据,合理分配两种可信度模型的选样数量对Co-Kriging方法构造的代理模型的近似精度以及计算代价至关重要。为此使用两个函数算例开展选样方案研究,针对不同数量的高、低可信度样本数据构造了三种代理模型进行对比,a)使用Kriging方法和高可信度样本数据直接构造高可信度模型的近似(Kriging);b)使用Kriging方法和高、低可信度样本数据的差值构造差值的近似,再加上低可信度模型的值作为高可信度模型的近似(Delta-Kriging);c)使用Co-Kriging方法和变可信度模型样本数据作为高可信度模型的近似(Co-Kriging)。为了进行代理模型的近似误差对比,利用拉丁超立方方法选取独立的检验数据,误差选为均方相对误差(Mean Relative Square Error,MRSE)
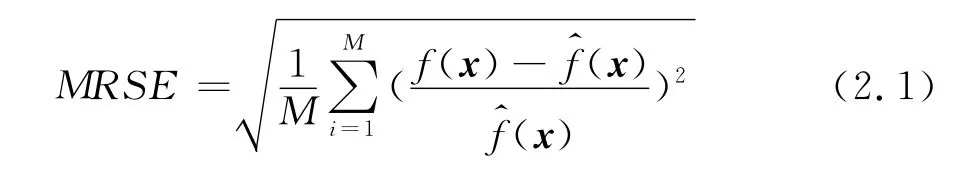
及最大相对误差(Max Relative Error,MRE)作为检验代理模型预测误差的标准
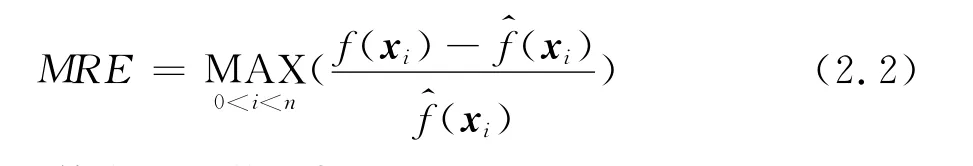
2.1 单变量函数分析
假设高可信度模型为函数fe(x)=(7x-1)2sin(14x-4),x∈{0,1)。低可信度模型可以表达为fc(x)=Afe+B(x-0.5)-C其中A=0.4,B=10,C=-5。由于问题非常简单,样本点的选取是认为指定的,通过测试得知nsh=4,nsl=11时,Co-Kriging方法就可以得出与真实函数吻合的近似结果(如图1)。当高可信度模型的选样数量nsh=4即3nv+1时,不同低可信度选样数量nsl的近似结果如图1,可见Co-Kriging对低可信度样本数量非常敏感,较少的低可信度样本数量的近似结果反映不了真实函数的基本趋势,而低可信度模型的样本数量nsl=11即达到10nv+1时,又可以得到与真实函数完全吻合的近似结果。当低可信度模型的选样数量足够11nv+1时,不同高可信度选样数量nsh的近似结果如图2,Co-Kriging变可信度代理模型只需要较少的高可信度样本(3nv+1)就可以得到与真实函数吻合的近似结果,Kriging模型和Delta-krigng模型则需要更多的高可信度样本(10nv+1)。在高可信度模型样本不足时,Delta-Kriging模型的近似结果要比Kriging模型的更精确。
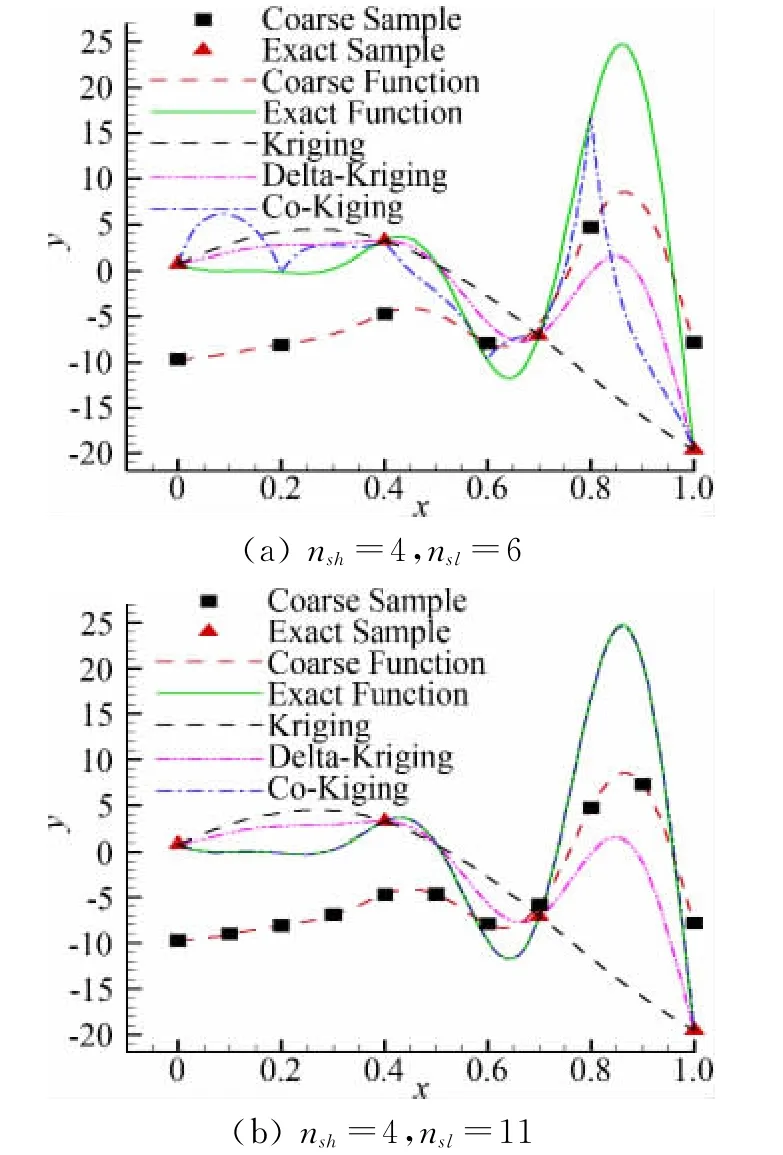
图1 低可信度选样数量对代理模型预测结果的影响Fig.1 The influence of number of low-fidelity samples
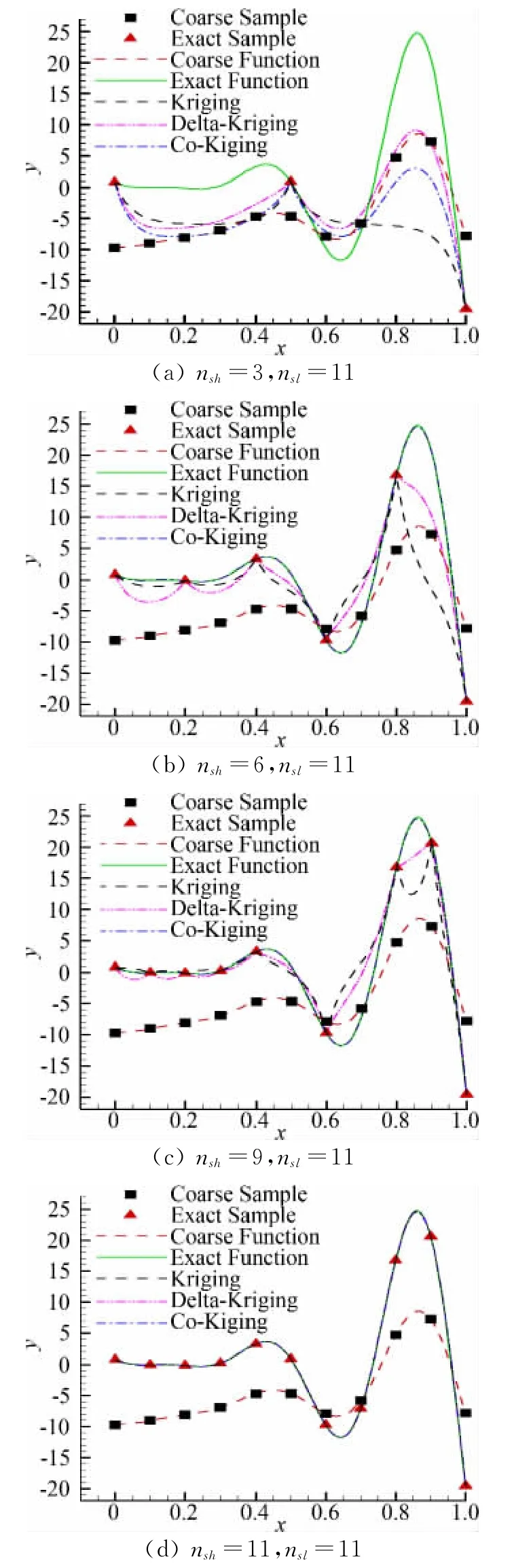
图2 高可信度选样数量对代理模型预测结果的影响Fig.2 The influence of number of high-fidelity samples
2.2 双变量函数
高可信度模型为函数fe(X)=20++x-10cos(2πx1)-10cos(2πx2),x1,x2∈[0,2]。该函数是一个具有多峰值的双变量函数,构造的低可信度模型则表达为fc(X)=Afe+B(x1+x2-0.5)-C。其中A=0.6,B=5,C=1。由于问题的复杂度增加,样本的选取采用了拉丁超立方方法(Latin Hypercube Method),给定较多高可信度选样数量时nsh=5nv+1,不同低可信度选样数量nsl的近似结果如图3,可见当问题复杂度提高时Co-Kriging方法对低可信度样本数量要求很高,需要低可信度样本数量nsl达到35nv+1,才能得到与真实函数吻合的近似结果。
图3 低可信度选样数量对代理模型预测结果的影响Fig.3 The influence of number of low-fidelity samples
在低可信度选样数量足够时nsl=35nv+1,不同高可信度选样数量nsh的近似结果如图4,使用Co-Kriging方法只需要3nv+1的高可信度样本就可以得到满意的近似结果。可见问题的复杂程度决定Co-Kriging方法对低可信度模型的选样数量,而对高可信度模型需要的样本数量影响不大,由于低可信度模型的计算时间和资源消耗都很廉价,Co-Kriging方法可以大大减少构造高精度代理模型的代价。
3 气动优化算例
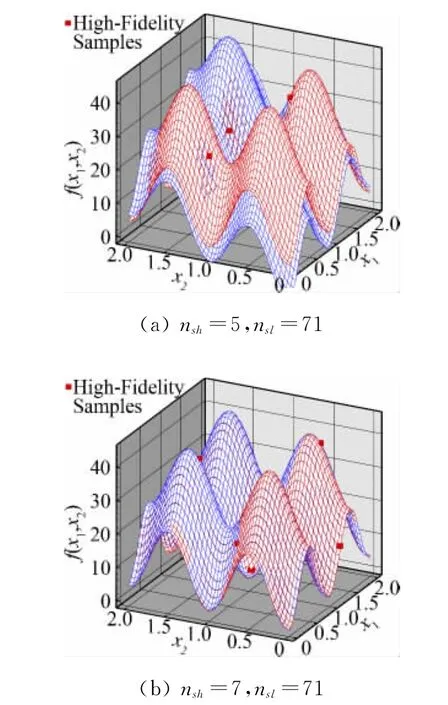
图4 高可信度选样数量对代理模型预测结果的影响Fig.4 The influence of number of high-fidelity samples
由于测试函数体现不出复杂工程优化问题的非线性特性,因此进行一个RAE2822翼型减阻优化算例来进一步证实Co-Kriging方法的特性,计算状态为M=0.729以及攻角α=2.31°。为了进行翼型的气动特性计算,将全速度势方程解作为低可信度模型,而把RANS方程的数值解作为高可信度模型。翼型采用Hicks-Henne方法进行参数化,总的设计变量个数为12个。根据函数算例的结果,使用拉丁超立方方法(Latin Hypercube Method)选取了150个低可信度样本。
图5为代理模型对升力系数预测结果的对比,基于差值的Delta-Kriging变可信度模型在样本数量较少时其近似精度要比Kriging模型高,但随着样本数量的增加,其预测精度与Kriging模型的越来越一致,Co-Kriging变可信度模型在大量低可信度数据的辅助下使用很少的高可信度样本就得到了很高的近似精度,这说明基于高、低可信度差值的Kriging模型可以提取的高低可信度模型间的关系信息很有限,而Co-Kriging方法可以充分挖掘低可信度模型的信息,大大提高了代理模型的效率,在基于高精度复杂数值模拟的优化设计时带来极大的好处。
利用遗传算法进行了基于代理模型和RANS方程数值模拟的翼型减阻优化,优化中对翼型的最大厚度以及升力系数进行约束。遗传算法的种群规模为100,优化进行了30代,优化模型为:
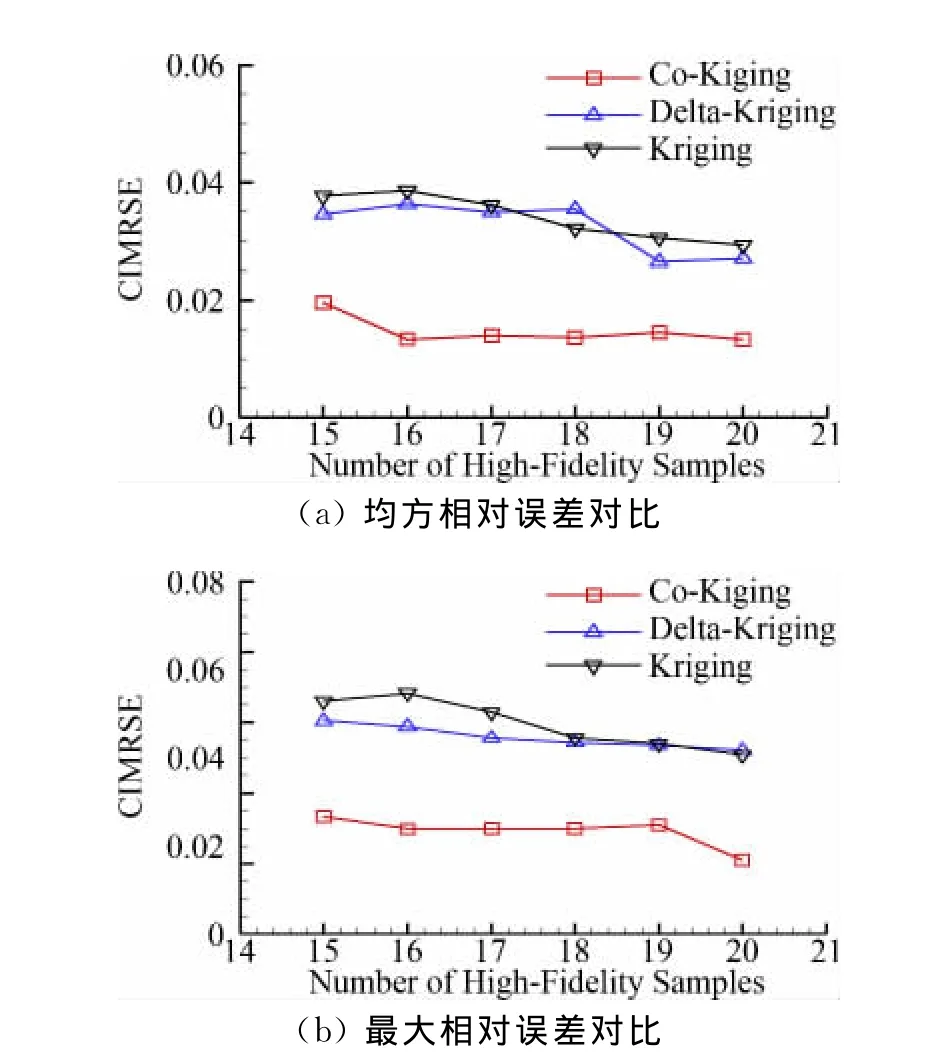
图5 代理模型预测误差对比Fig.5 Comparison of lift coefficient approximation
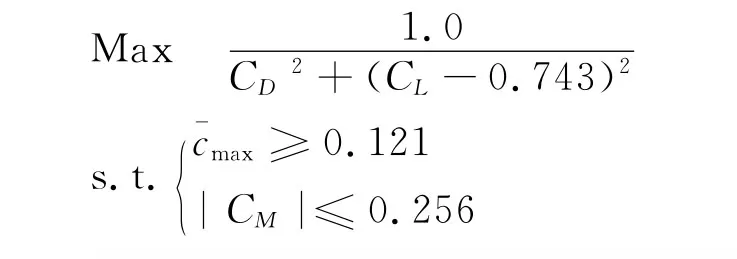
CD、CL、CM分别为翼型的阻力系数、升力系数和俯仰力矩系数。目标函数的设置是期望升力系数尽量靠近0.743,同时最小化阻力,并且对控制翼型的最大厚度max和俯仰力矩系数进行约束。基于代理模型的优化中对每一代的最优解进行验证并更新代理模型,优化后的翼型形状和压力分布如图6,可见基于Co-Kriging变可信度模型的优化结果与基于RANS方程数值模拟(即高可信度模型)的优化结果基本一致,优化后翼型的激波得到了极大地削弱。而基于Kriging模型的优化结果虽然也削弱了激波,但是比另外两种方法的要强一些。这说明利用足够的低可信度样本数据(大于10nv+1)和少量高可信度样本数据构造的Co-Kriging变可信度代理模型可以给出更好的近似结果和正确的优化方向,同时大大减少了优化过程的计算代价,可以满足工程设计优化的需要并提高优化设计过程的效率。
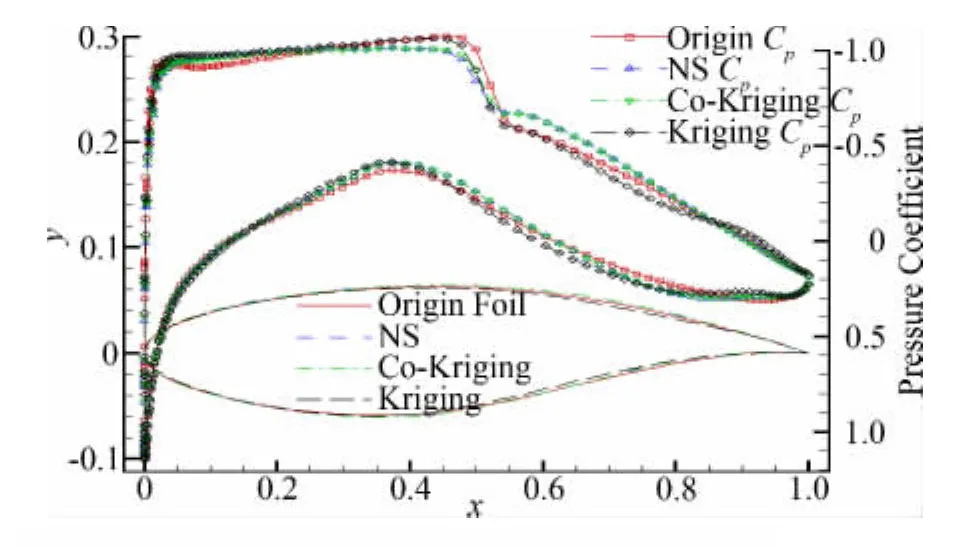
图6 优化结果翼型和压力分布Fig.6 The optimized airfoil and pressure coefficient distribution
4 结 论
本文利用Co-Kriging方法构造了一种高效的变可信度代理模型,可以利用大量低可信度模型数据来增强模型的预测能力,提高代理模型的效率,在高可信度数据难以获取时可以带来极大的好处。代理模型的近似精度与样本数量和样本可信度直接相关,使用单变量函数和双变量函数算例对代理模型进行的选样方案研究表明,Co-Kriging方法比Kriging方法更加高效,只要超过3nv+1就可以得到合理近似精度,其所需低可信度模型数据则要随着问题的复杂程度不断增加。用遗传算法进行的基于代理模型的翼型减阻优化结果证实Co-Kriging变可信度代理模型更加高效,其优化结果和使用高可信度模型直接进行优化的结果基本一致,能够满足工程设计优化的需要。
[1]IKJIN LEE,CHOI K K,ZHAO L.Sampling-based RBDO using the dynamic Kriging(D-Kriging)method and stochastic sensitivity analysis[A]//13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference[C].Fort Worth,Texas,2010.AIAA 2010-9036.
[2]ALLAIRE D,WILLCOX K.Surrogate modeling for uncertainty assessment with application to aviation environmental system models[J].AIAAJournal,2010,48(8):1791-1803.
[3]阎平凡,张长水.人工神经网络与模拟进化计算[M].清华大学出版社,2005.
[4]BUHMAN N,MARTIN D.Radial basis functions:theory and implementations[M].Cambridge university press,2003.
[5]SACKS J,WELCH W J,MICHELL T J,WYNN H P.Design and analysis of computer experiments[J].StatisticalScience,1989,4(4):409-435.
[6]GIBBS M N.Bayesian Gaussian processes for regression and classification[D].[PhD Thesis].University of Cambridge,1997.
[7]MYERS R,MONTGOMERY D.Response surface methodology[M].New York:John Wiley & Sons,Inc.,1995.
[8]ZIMMERMANNL R,GORTZ S.Non-linear reduced order models for steady aerodynamics[J].ProcediaComputerScience,2010,1:165-174.
[9]LEIFSSON L,KOZIEL S.Multi-fidelity design optimization of transonic airfoils using physics-based surrogate modeling and shape-preserving response prediction[J].JournalofComputationalScience,2010(1):98-106.
[10]DANIEL M J,GEOFFREY T P,WILLIAM N D,et al.Robust multi-fidelity aerodynamic design optimization using surrogate models[R].AIAA 2008-6052.
[11]FORRESTER A I J,So′BESTER A,KEANE A J,et al.Multi-fidelity optimization via surrogate modeling[J].ProceedingsoftheRoyalSocietyA.,2007,463(11):3251-3269.
[12]MYERS D E.Matrix formulation of Co-Kriging[J].MathematicalGeology,1982,14(3):249-257.
[13]SHAWN E G,HAROLD K,DON E B II.Comparison of three surrogate modeling techniques:datascaper,Kriging,and second order regression[R].AIAA 2006-7048.
[14]MARTIN J D,SIMPSON T W.Use of Kriging models to approximate deterministic computer models[J].AIAAJournal,2005,43(4):853-863.
[15]张德虎,高正红,李焦赞,等.基于双层代理模型的无人机气动隐身综合设计[J].空气动力学学报,2013,31(3):394-400.

