大跨桥梁抖振力与脉动风速空间相关性的对比研究

李少鹏，李明水，马存明，廖海黎

（西南交通大学 风工程试验研究中心，四川 成都 610031）

0 引 言

大跨度桥梁可以视为一种细长结构，传统的抖振分析一般基于片条假设，近似认为脉动风及其引起的非定常气动力具有线性关系，即抖振力的空间相关性与脉动风的空间相关性是等价的［1］。研究结果表明，对于大跨桥梁，脉动风的顺风向积分尺度（大约100m～200m）至少10倍于结构的特征尺寸，因此紊流引起的非定常阻力可以采用片条假设较为精确的描述。而脉动风的竖向积分尺度（大约30m～50m）与桥宽接近，因而抖振升力与抖振力矩的跨向分布则不能用片条假设精确描述［2］，这也是桥梁抖振精细化研究的一个重要方向。

Roberts认为在风洞中由格栅产生的紊流是各项同性的，其脉动风谱可以用Von Karman谱良好的拟合，并据此提出了适用于各向同性紊流的空间相关性计算方法［3］。Mann等人也提出了类似的、计算各向同性紊流空间相关性的计算公式［4－6］。李等［7］基于经典空气动力学理论进一步研究了各向同性紊流下抖振力的空间相关性，定义了抖振力和脉动风空间交叉谱以及无量纲相干函数的一般表达式，并通过实际算例验证了其理论的有效性。Larose［8－9］和马［10］运用尖塔、格栅形成紊流场，通过节段模型测压试验，直接测得表面压力分布，将测点压力沿断面积分即可得到该截面的抖振力，进而研究抖振力的跨向相关性，试验表明，对于箱形断面，抖振力的跨向相关性大于脉动风的相关性。

在Larose等人的节段模型测压试验中，由于风洞试验段尺寸以及模型缩尺比的限制，故采用的试验段长度较小，其中，Larose节段模型试验段长度0.3m，马［10］的试验段长度0.48m，因此以上试验均无法反映较长跨向间距内抖振力的跨向相关性。而且以上试验成果均反映的是风洞被动模拟紊流场下抖振力的跨向相关性，而风洞试验结果能否反映自然大气紊流下抖振力的跨向相关性尚无定论。为了突破上述试验瓶颈，进一步研究抖振力的跨向分布规律，理论分析方法可成为解决这一难题的有效手段之一。

本文将以抖振升力为例，通过理论分析手段，建立能够合理描述抖振力跨向相关性的数学模型，并与Larose的试验结果进行对比，进而得到抖振力跨向相关性的一般规律。本文的研究成果可以推广到抖振力矩与阻力的跨向相关性研究之中。

1 抖振力跨向相关性数学模型

基于各向同性紊流假设，以升力为例，抖振力及脉动风的跨向相关性以互相关系数来表示：

式中，ΦjAB为A、B两点的互相关系数（j＝1表示抖振升力，j＝2表示纵向脉动分量，j＝3表示竖向脉动分量）；CovjAB为A、B两点的协方差；σjA、σjB分别为A或B点的均方根；SjAB为A、B两点的互谱；SjA、SjB分别为A、B点的点谱。

对于各向同性紊流，可以认为σjA＝σjB，即SjA＝SjB（j＝1～3），因此下文用Sj来表示任意两点的点谱。由此式（1）可以化简为如下形式：

式中，j＝1～3，意义同上。

Larose定义如下形式的抖振升力模型：

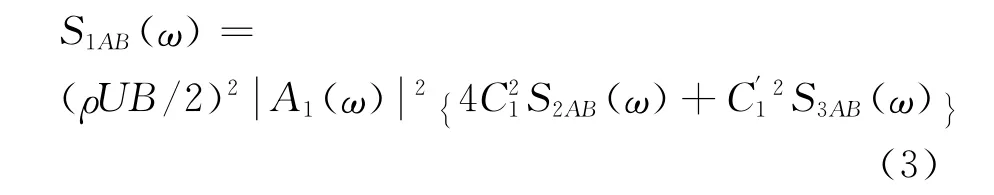
式中，S1AB、S2AB及S3AB的定义与式（1）相同；A1为气动导纳函数；C1为升力系数；表示升力系数导数。

式（2）中气动导纳采用Sears函数形式的Liepmann［11］近似表达式：

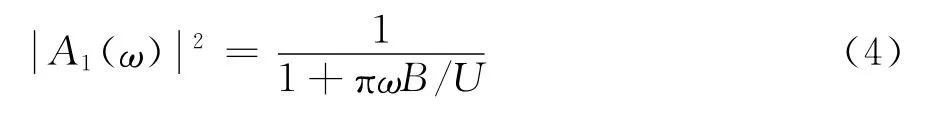
式中，B为桥宽，U为平均风速。

本文采用李等［4］提出的脉动风互谱计算公式：

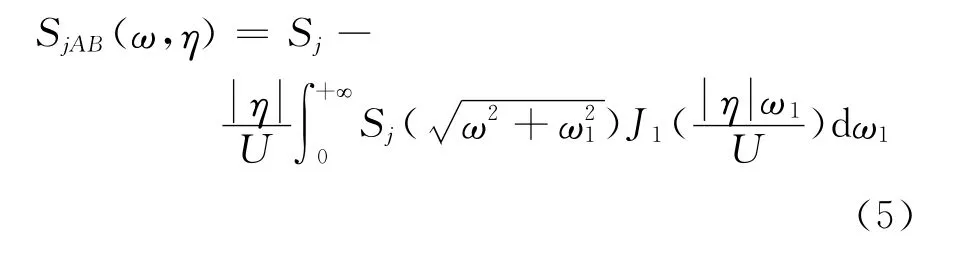
式中，j＝2或3，分别表示纵向及竖向脉动分量；η为A、B两点距离；U为主梁水平高度处的平均风速；J1（ω）为第一类Bessel函数。

在此，以Von Karman谱表示风洞模拟风谱，以基于大量实测而建立的自然大气功率谱Simiu谱［12］和Panofsky谱［13］分别表示纵向、竖向自然大气风谱，根据式（2）～式（5），分别对两类风谱下抖振力及脉动风沿跨向的互相关系数进行数值积分，由此可得其精确解。

Von Karman谱［14］如下表示：

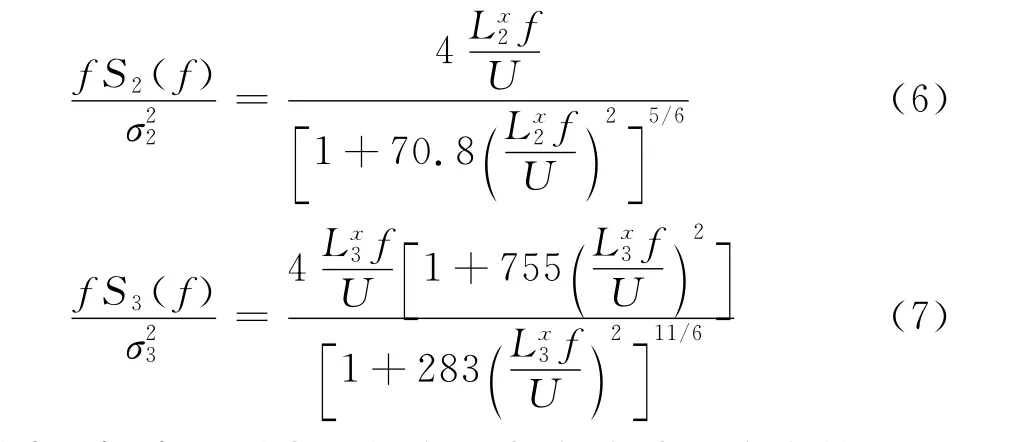
式中，、分别表示纵向及竖向脉动风均方值；、分别为纵向和竖向脉动风积分尺度。

对于各向同性紊流，一般认为：＝以及＝／2，但 Bearman［15］发现风洞试验产生的各向同性紊流满足＝1.46，因而竖向 Von Karman谱可以表示为：

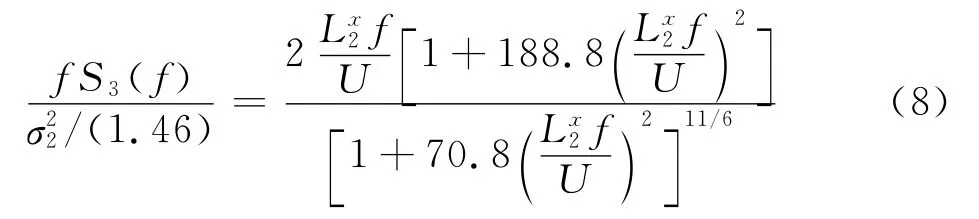
Simiu谱如下表示：

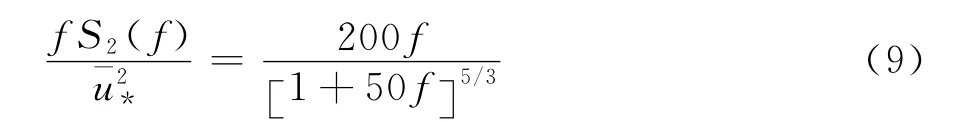
式中，f＝nz／U；为剪切速度均方值。

Panofsky谱如下表示：

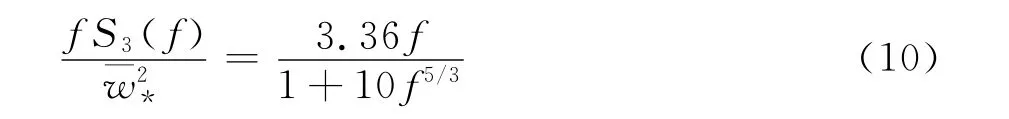
式中，f＝nz／U为剪切速度均方值，对于各向同性紊流，可近似认为≈。

将式（6）～式（10）代入式（2）～式（5），可得抖振力及脉动风沿跨向互相关系数的一般性表达式：

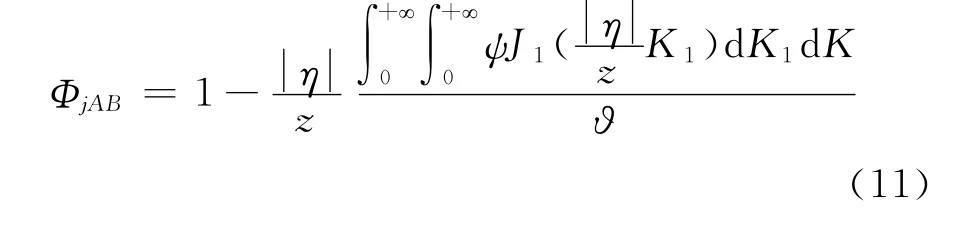
式中，j＝1～3；ψ、ϑ为待定参数；K＝为无量纲折减频率（对于自然大气风谱，z表示高度；对于风洞模拟风谱，z表示纵向积分尺度Lu）。

对于不同类型的风谱，只需改变参数ψ、ϑ即可得到抖振力以及脉动风沿跨向的互相关系数，在风洞模拟风谱以及自然大气风谱下，ψ、ϑ的取值分别如下：

对于纵向Von Karman谱：

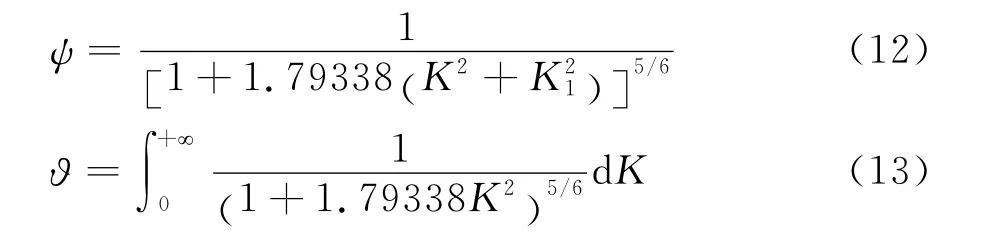
对于竖向Von Karman谱：

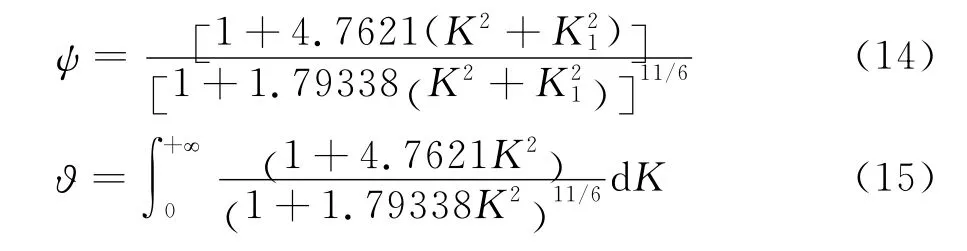
基于风洞试验风谱的抖振力：

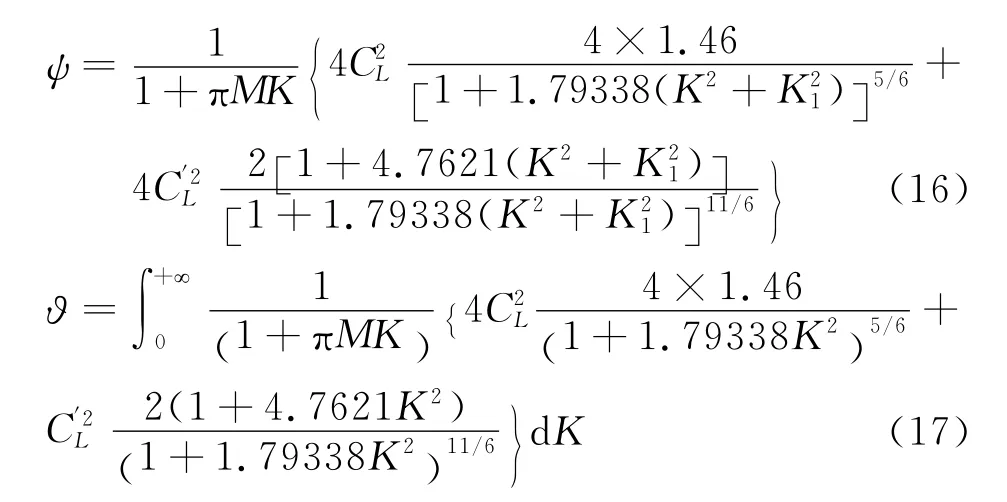
式中，M＝B／z；z为主梁水平高度。

对于Simiu谱：

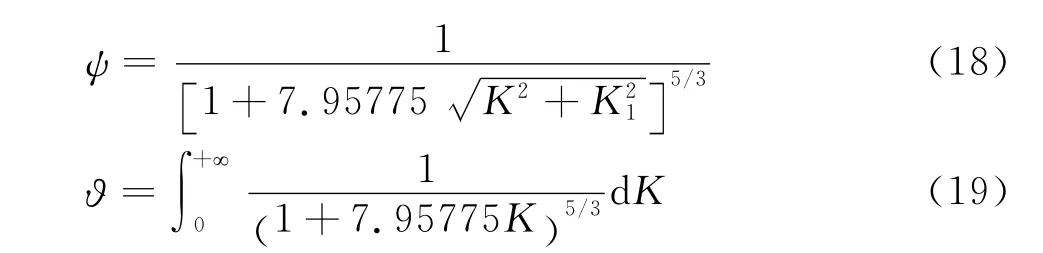
对于Panofsky谱：

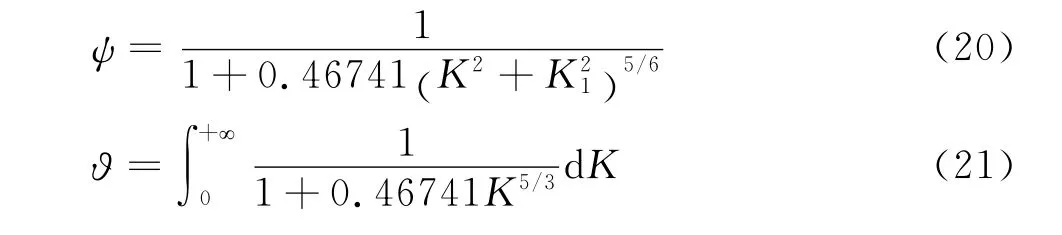
基于自然大气风谱的抖振力：

不同的跨向间距内，在风洞模拟风谱下抖振力及脉动风的跨向相关系数分别如图1、图2所示，为了清晰表示，图2横坐标采用对数坐标。

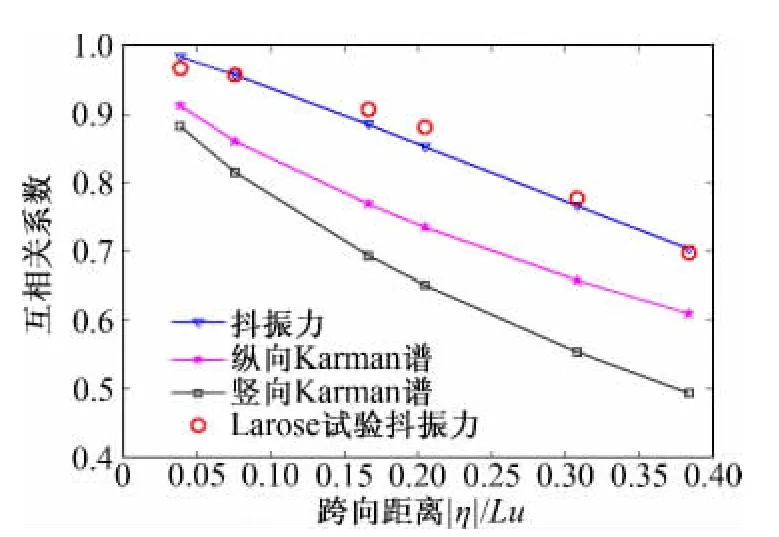
图1 风洞模拟风谱下抖振力及脉动风的互相关系数Fig.1 Cross－correlation coefficient of buffeting force ＆turbulence based on tunnel wind spectrum

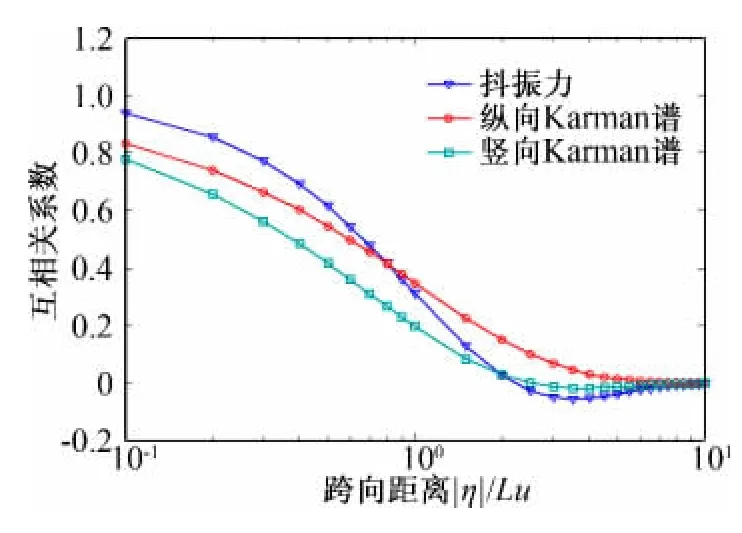
图2 风洞模拟风谱下抖振力及脉动风的互相关系数Fig.2 Cross－correlation coefficient of buffeting force ＆turbulence based on tunnel wind spectrum

自然大气风谱下抖振力与脉动风的跨向相关系数如图3所示：

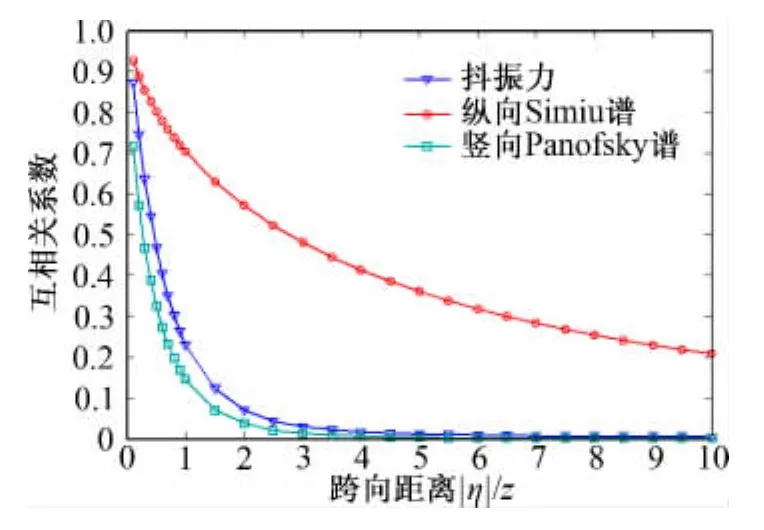
图3 自然大气风谱下抖振力与脉动风互相关系数Fig.3 Cross－correlation coefficient of buffeting force ＆turbulence based on natural wind spectrum

综合图1～图2结果可以得出，在风洞模拟风谱下，抖振力的跨向相关性高于脉动风的相关性这一结论仅在一定的跨向间距内成立。由图1所示，在较小间距内，理论计算得到的抖振力互相关系数与Larose的风洞试验结果很好的吻合。但是，如图2所示，随着跨向距离的增大，抖振力的跨向相关性逐渐低于脉动风的跨向相关性，并介于纵向与竖向脉动风的相关性之间。而在自然大气风谱下，由图3可以清晰的反映出抖振力的跨向相关性介于纵向脉动风与竖向脉动风的相关性之间。

由此，可以大胆推断，抖振力的跨向相关性高于脉动风的相关性这一论断成立是有一定限定条件的，即在风洞试验产生的紊流场中，其仅在一定的跨向间距内成立；而在自然大气紊流场中，抖振力的跨向相关性则介于纵向脉动分量与竖向脉动分量的相关性之间。

2 基于Davenport相干函数经验公式的抖振力跨向相关性

由于自然大气中的脉动风不符合各向同性紊流假设，为了进一步验证上述推断的有效性，下面采用Davenport提出的相干函数经验公式来求解自然大气风谱下抖振力的跨向相关性。

Roberts［3］和 Houblt［16］都曾定义过如下形式的空间谱的相关系数函数：

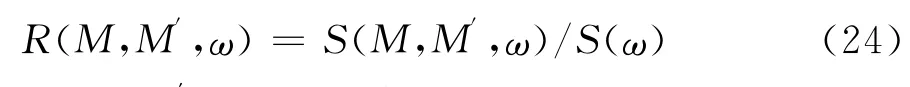
式中，M和M′为空间任意两点。

按照上述定义，本文采用下式来计算两点脉动风的互谱：

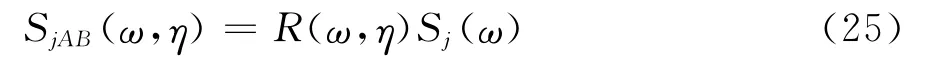
式中，j＝2～3，分别表示纵向及竖向脉动分量；R（ω，η）为相干函数，这里采用Davenport［17］相干函数经验公式：

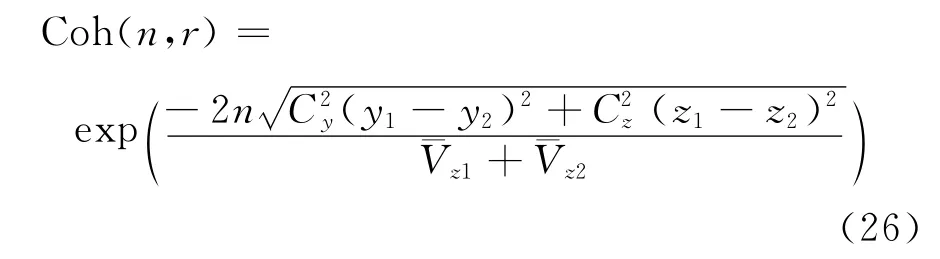
式中，n为频率；r为空间两点距离；y1、y2、z1、z2分别为空间两点的横向坐标和竖向坐标；1、2分别为高度z＝z1和z＝z2处的平均风速；Cy、Cz分别为与横向及竖向相关的指数衰减系数，Cy和Cz一般可取Cy＝8，Cz＝7。

考虑到桥梁主梁的高度较小，近似地认为整个主梁在同一水平高度上，即z1＝z2；则式（26）可以化简如下：

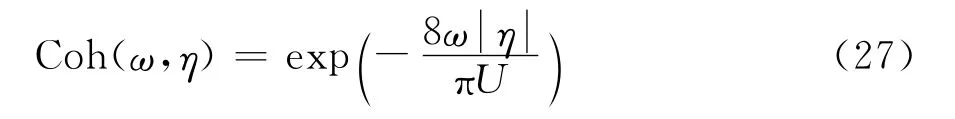
式中，η为跨向距离，U为主梁水平高度处平均风速。

将式（27）代入式（25）即可得到空间两点抖振力及脉动风的互谱：

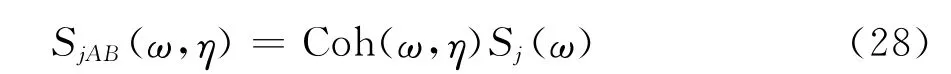
将自然大气风谱及式（28）代入式（2）即可得到此风谱下的抖振力和脉动风的跨向互相关系数，分析结果如下所示：

对于Simiu谱：

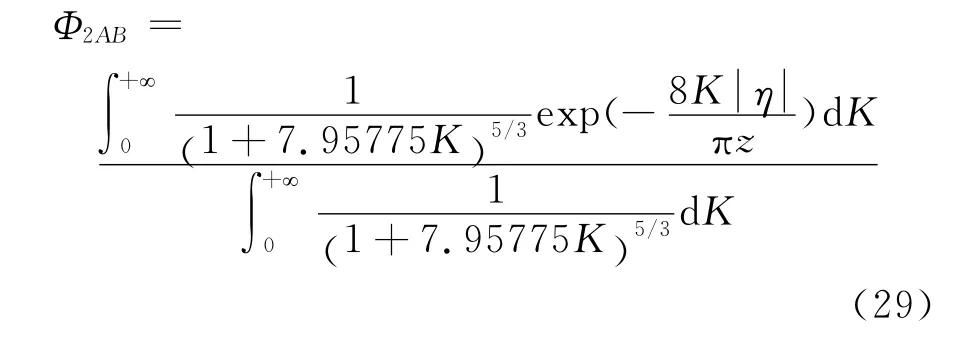
对于Panofsky谱：

基于自然大气风谱的抖振力参数如下所示：

由式（29）～式（31）可得自然大气风谱下抖振力及脉动风的跨向互相关系数如下所示。

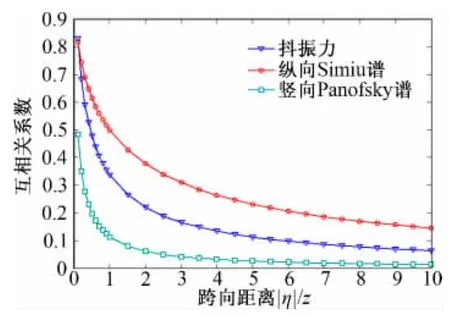
图4 基于经验相干函数的抖振力及脉动风互相关系数Fig.4 Cross－correlation coefficient of buffeting force ＆turbulence based on empirical coherence function

对比图3、图4可以发现，根据Davenport相干函数经验公式得到的抖振力及脉动风的互相关系数与第2节理论计算结果趋势一致，由此可以验证在自然大气紊流场中本模型的有效性。

3 结 论

本文通过理论分析方法，深入研究了抖振力与脉动风在不同流场以及较大跨向间距范围内的跨向相关性，由此可以得以下结论：

（1）在风洞模拟紊流场中，在较小的跨向间距内，抖振力的跨向相关性高于脉动风的相关性，并与Larose试验结果吻合，而随着跨向间距的增大，抖振力的跨向相关性逐渐低于脉动风的相关性。

（2）在自然大气紊流场中，抖振力的跨向相关性介于纵向脉动风与竖向脉动风的相关性之间。

［1］DAVENPORT A G.The application of statistical concepts to the loading of structures［J］.ICEProceedings，1961，19（4）：449－472.

［2］LAROSE G L.The spatial distribution of unsteady loading due to gusts on bridge decks［J］.JournalofWindEngineeringandIndustrialAerodynamics，2003：1431－1443.

［3］ROBERTS J B，SURRY D.Coherence of grid generated Turbulence［J］.JournalofEngineeringMechanics，ASCE，1973，99（6）：1227－1245.

［4］MANN J.The spatial structure of neural atmospheric surface－layer turbulence［J］.JournalofFluidMechanics，1994，273：141－168.

［5］MANN J，KRISTENSEN L，COURTNEY M S.The great belt coherence experiment－a study of atmospheric turbulence over water［R］.Riso Report R－596，1991：51.

［6］FORSCHING H W.气动弹性力学原理［M］.沈克扬，译.上海科技出版社，1981：695－696.

［7］李明水，贺德馨，王卫华.大跨度桥梁抖振响应的频域分析［J］.空气动力学学报，2000，18（1）：74－80.

［8］LAROSE G L，TANAKA H，GIMSING N J，et al.Direct measurement of buffeting wind forces on bridge decks［J］.JournalofWindEngineeringandIndustrialAerodynamics，1998，74－76：809－818.

［9］LAROSE G L.Gust loading on streamlined bridge decks［J］.JournalofFluidandStructures，1998，12（5）：511－536.

［10］马存明.流线箱型桥梁断面三维气动导纳研究［D］.［博士论文］.西南交通大学，2007.

［11］LIEPMANN H.On the application of statistical concepts to buffeting problem［J］.JournalofAeronautical Science，1952，19（12）：793－800.

［12］SIMIU E.Wind spectra and dynamic alongwind response［J］.JournaloftheStructuralDivision，1974，100：1897－1910.

［13］BUSH N E，PANOFSKY H A，Recent spectra of atmospheric turbulence［J］.TheQuarterlyJournaloftheRoyal MeteorologicalSociety，1968，94（400）：132－148.

［14］SHIAU B S.Velocity spectra and turbulence statistics at the northeastern coast of Taiwan under high－wind conditions［J］.JournalofWindEngineeringandIndustrialAerodynamics，2000，88（2）：139－151.

［15］BEARMAN P W.Some measurements of the distortion of turbulence approaching a two－dimensional bluff body［J］.JournalofFluidMechanics，1972，53（3）：451－467.

［16］HOUBLT J G.On the response of structural having multiple random inputs［R］.WGLR－Jahrbuch 1957，1958.

［17］DAVENPORT A G.The dependence of wind load upon meteorological parameters［A］.Proceedings of the international research seminar on wind effects on building and structures［C］.University of Toronto Press，1968：19－82.