高斯射线束叠前深度偏移成像研究
谢 飞,李 佩,黄中玉,3,魏修成,3,朱成宏
(1.中国石油化工股份有限公司石油勘探开发研究院,北京 100083;2.中国地质大学(北京),北京 100083;3.中国石油化工集团公司多波地震重点实验室,北京 100083)
在复杂介质条件下,叠前深度偏移技术能提供很好的构造成像结果。Kirchhoff积分叠前深度偏移方法以其灵活的目标处理功能,高效的数值计算和对空间非规则采样数据的适应能力等特点,在石油工业界得到了广泛应用。然而,对于由复杂构造引起的多值走时、阴影、焦散等问题,采用Kirchhoff偏移方法成像效果往往不如单程波方法。高斯束偏移方法是Kirchhoff偏移方法的改进,既具备Kirchhoff偏移方法的灵活性和适应性,又能解决焦散、多值走时等问题,其成像效果堪比单程波算子,同时还能克服单程波算子的倾角限制,成像回转波[1-6]。
Hill[7]提出了叠后高斯束偏移方法,通过局部的倾斜叠加将波场分解为高斯束。对每个高斯波束偏移成像、叠加得到最终的偏移结果。Hale[8-9]详细分析了Kirchhoff偏移、倾斜叠加偏移和高斯束偏移的关系,指出高斯束偏移与Kirchhoff偏移、倾斜叠加偏移相比的优点,并给出了具体的计算公式,分析了其计算效率。
Hill[10]给出了叠前高斯束偏移的方法。在共偏移距偏移中,通过对所有偏移距射线参数进行扫描找到使总走时虚部最小的炮点射线参数和检波点射线参数的组合。这种扫描可以在稀疏的偏移成像点网格上执行,然后将值再内插到较密集的成像网格点上,因此具有较高的计算效率和精度。
Gray[11]指出由Hill提出的共偏移距偏移方法对于较规则的观测系统是合适的,但是对于其它观测系统的记录,或者是地表高程变化大、近地表速度变化剧烈时不利于成像。Gray提出炮集高斯束偏移更适合陆地起伏地表的地震数据。
1 高斯束偏移方法原理
假设地震波场满足标量波动方程:
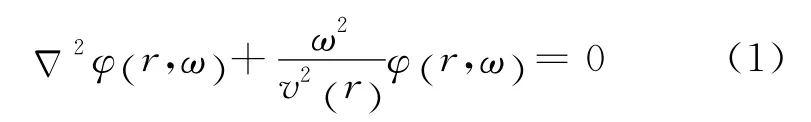
则可将由r′点源激发传播到r点的地震波场表示为瑞雷积分形式:
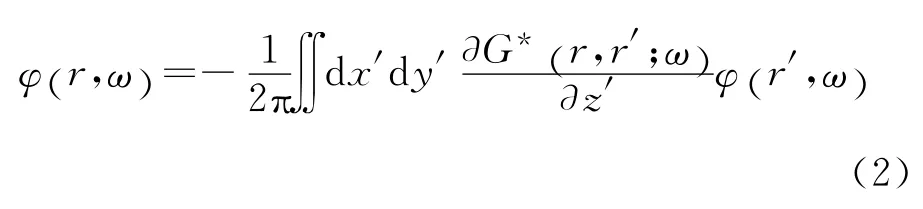
Hill[10]的研究表明,点源波场的格林函数可用高斯射线束的积分形式表示:
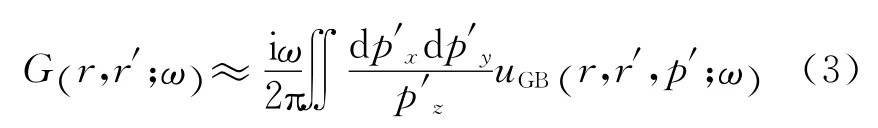
其中,uGB(r,r′,p′;ω)为在r′点激发、方向为p′的射线束。因此,当将(2)式中的格林函数用(3)式的高斯束形式表示时,就可以得到利用高斯束表示的地震波场。
当射线束的中心不在r′点而在邻近的r0点时,由于在高斯束发射的初始位置波束是特定传播方向的平面波波场,Hill[10]引入相移因子exp[-iωp′(r′-r0)],则r′点到r点的格林函数表示为
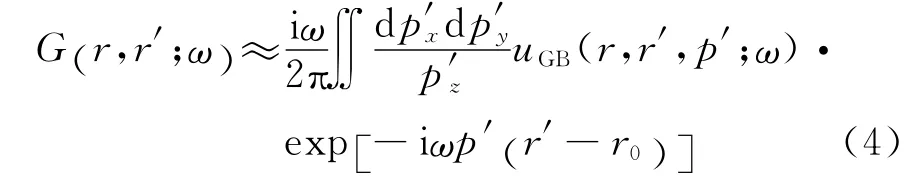
在克希霍夫积分公式(2)中使用格林函数(4)时,应该将公式(2)中的积分范围划分为小的空间积分窗,并且保证在计算格林函数(4)时,空间积分窗的中心r0点与积分窗内的任意点r′相距不远,能保持初始高斯束的平面波性质,为此,Hill[10]引入了如下高斯函数:
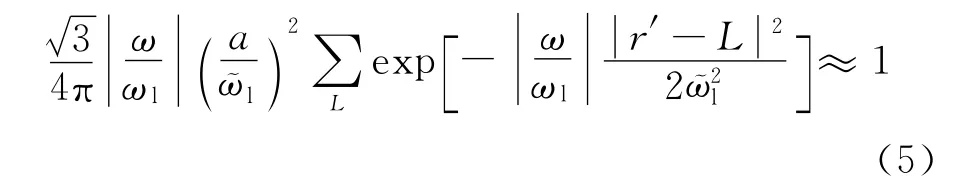
其中,ωl是参考频率是射线束宽度;a是网格点最小间距。并得到了地震数据局部倾斜叠加的频率域表达形式:
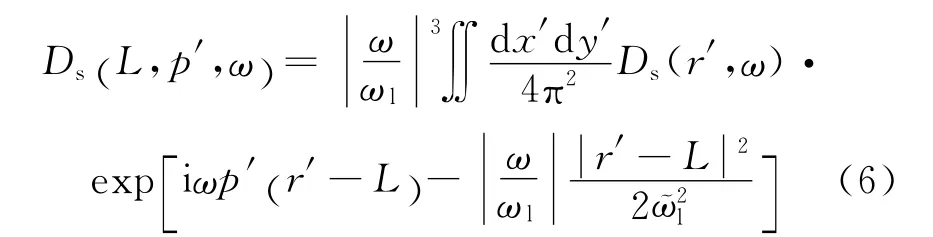
利用Claerbout[12]的相关成像原理,将炮点波场和检波点波场均按照克希霍夫积分公式向下延拓,并将两个波场进行互相关可得到偏移成像公式:
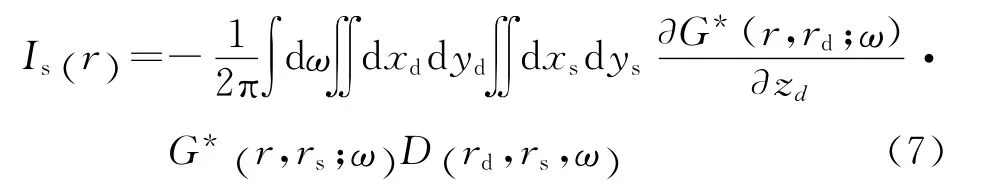
将偏移成像公式(7)中的格林函数用(4)式的高斯束表示,并结合高斯函数(5)式,就可以得到以高斯束形式表达的偏移成像公式:
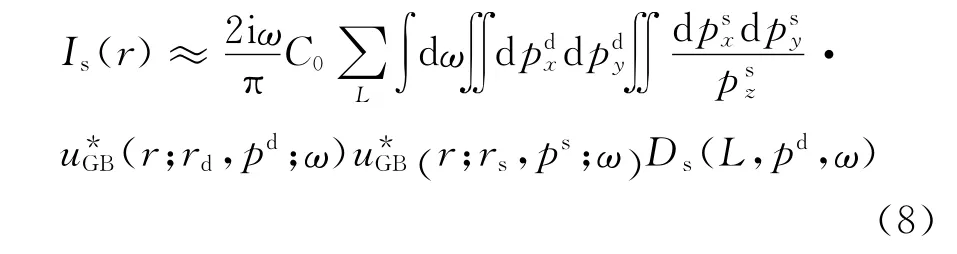
其中,C0是与高斯函数相关的系数。
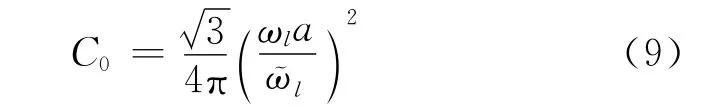
Hale[8]对克希霍夫、倾斜叠加和高斯束3种偏移方法进行了详细比较,揭示了三者间的联系与区别,认为在时间域做高斯束偏移要比在频率域效率高,并给出了单个高斯束对地下成像贡献的时间域表达式:
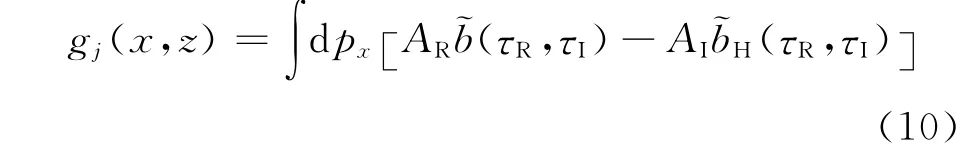
其中,AR和AI分别对应复值振幅的实部和虚部;τR和τI分别为复值走时的实部和虚部。复值振幅和复值走时均可通过高斯束射线追踪得到。px为射线参数,代表倾斜叠加形成的平面波传播方向;(τR,τI)为高斯窗内地震数据的倾斜叠加结果;(τR,τI)为(τR,τI)的Hilbert变换。(τR,τI)可由下式得到:
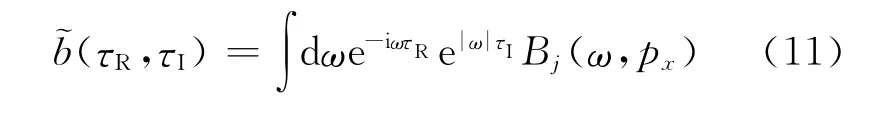
其中,Bj(ω,px)为第j个高斯窗内通过倾斜叠加得到的频率域结果,其具体表达式为
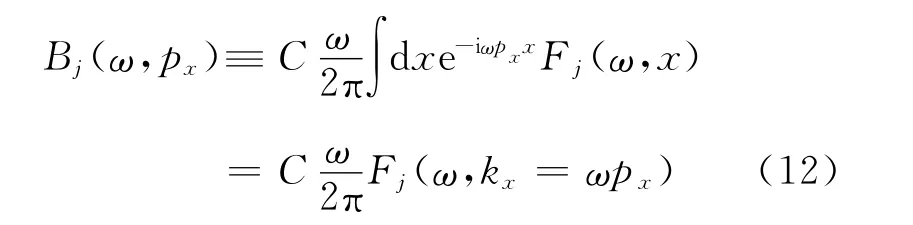
式中:C为与高斯窗函数相关的振幅系数;Fj(ω,kx)为地震记录fj(x,t)的二维Fourier变换。
关于高斯窗函数的空间间隔与波束射线参数采样间隔的关系,Hill[7,10]和Hale[8]均进行了详细的讨论,我们采用了Hill[7,10]给出的参数选取准则。
2 基于高斯射线束的角道集
角度域共成像点道集在AVA 分析和偏移速度分析方面有着非常广阔的应用前景。郭朝斌等[13]和李振春等[14]给出了利用粗网格走时信息计算角度域共成像点道集的方法。我们利用高斯束中心射线所携带的丰富的速度、方向信息,便捷直观地给出了角度域共成像点道集的计算方法。
在中心射线坐标系下,某一网格点处的走时可由对应的中心射线通过二阶泰勒展开得到[15](图1):
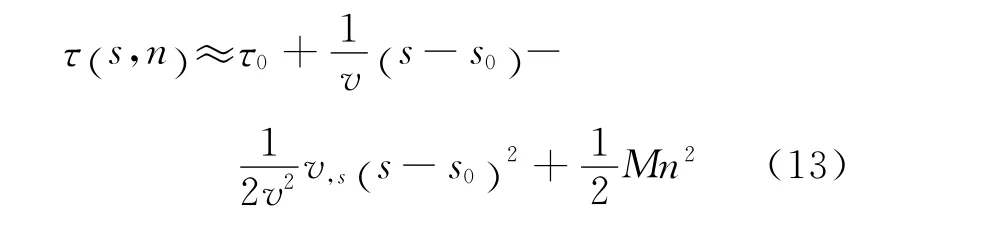
其中,τ0为中心射线走时;M可由动力学射线追踪得到。
利用坐标变换,将中心射线坐标系转换为直角坐标系,(13)式变为
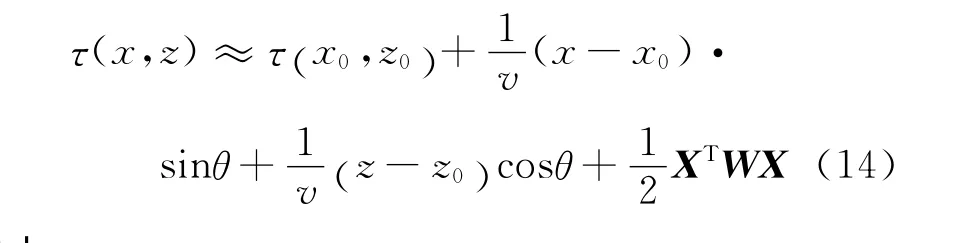
其中,

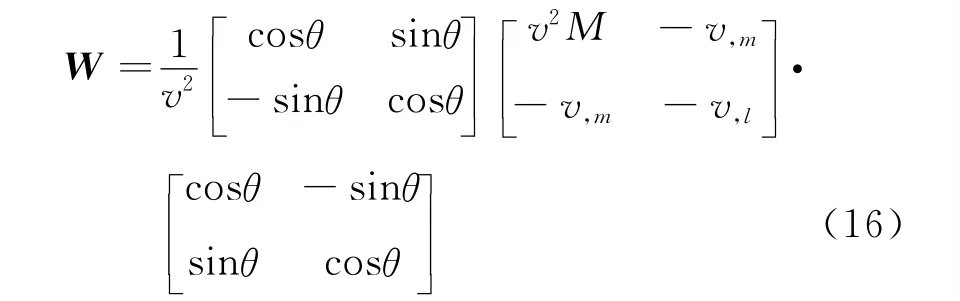
式中:θ表示射线方向与Z轴的夹角。由(14)式对走时分别计算X方向和Z方向的偏导数,得到慢度px和pz:
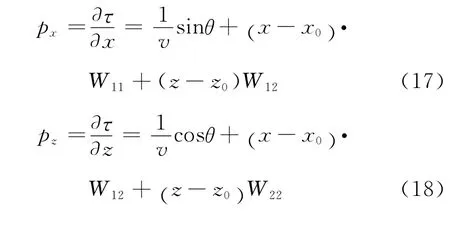
其中,
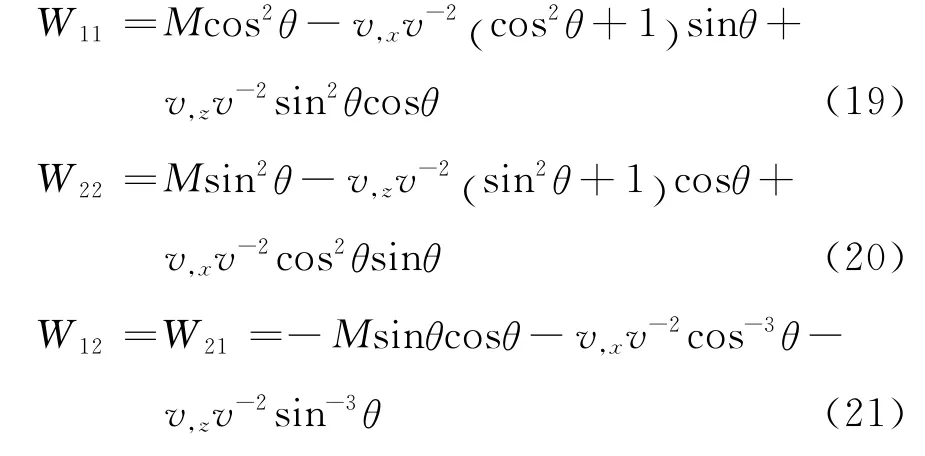
得到成像点处的水平和垂直慢度后,我们可以分别计算出来自炮点的入射波场的射线角度φs 和来自射线束中心点的反射波场的射线角度φr:
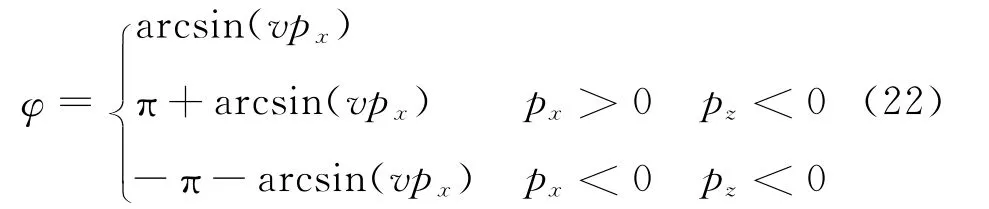
在分别计算出φs 和φr 后,可通过计算二者之间的夹角来得到孔径角。对于常规纵波勘探而言,反射角γ为孔径角的一半,即

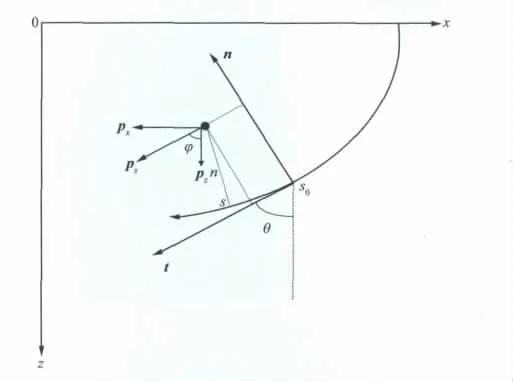
图1 由中心射线计算成像点走时和射线方向原理示意图解
3 模型测试
我们首先利用Marmousi国际标准模型对基于高斯束偏移的角度域共成像点道集算法进行了测试。
图2给出了Mamousi速度模型。图3给出了采用本文方法对Mamousi模型数据进行偏移得到的结果,可见成像效果良好。在输出时我们选择的角度范围为[-60°,60°],但由于观测系统为右边放炮左边接收,所以在[0,60°]基本没有能量,因此,我们只显示[-60°,0]的角度域道集(图4)。图4a对应图3中最左边的三角形位置,该处构造相对简单,呈现层状结构,对应的角道集也被拉平;图4b对应图3中间的三角形位置,图4c对应图3中最右边的三角形位置,这两处对应的构造复杂,横向变速剧烈,角道集也同样得到了拉平。由此可见,即使在如此复杂的构造条件下,算子的成像精度依然很高,保证了最终高质量的成像结果。

图2 Marmousi模型

我们设计了一个包含直立断层的复杂模型,该模型尺寸水平方向为27 000m,垂直方向为4 000m,其速度场如图5所示。利用有限差分技术模拟炮集记录,观测系统为中间放炮两边接收,检波点间隔为50m,炮点间隔为100m,偏移距范围为[-6 000m,6 000m],共110炮,第1炮炮点位置在8 000m处。
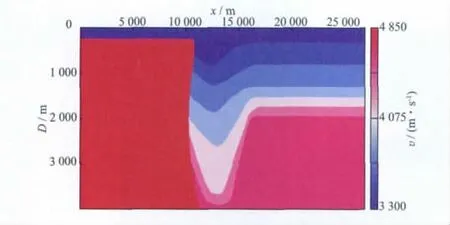
图5 包含直立断层的复杂构造速度模型
图6a和图6b分别给出了采用二阶广义屏偏移方法和高斯束偏移方法对该复杂模型的炮集记录进行偏移得到的结果。对比图6a和图6b可以看出,两种方法整体上均能对构造有比较好的成像效果,但是在陡倾角区域,高斯束偏移方法成像效果更好(图6中红色箭头、红色方框、红色椭圆所示位置),二阶广义屏偏移方法无法对直立断层进行成像,而高斯束偏移方法能够清晰、准确地对直立断层进行成像。
图7给出了图6中红色方框内偏移结果的局部放大显示。对比图7a和图7b可见,广义屏算法在陡倾角构造部位引入了较强的偏移噪声,而且没有将能量归位到正确的位置上;而高斯束偏移结果信噪比高,同时将能量归位到了正确的倾角构造位置上。但由于观测系统的原因,高斯束方法也未成像出中间的一段陡倾角构造。图8给出了图6中红色椭圆内偏移结果的局部放大显示。对比图8a和图8b可见,对于陡倾角构造,高斯束的偏移结果要比广义屏算法能量聚焦更好。
同时,我们对上述复杂构造模型采用二阶广义屏偏移和高斯束偏移的计算效率进行了对比,其结果如表1所示。可见,高斯束偏移的计算效率要明显高于二阶广义屏偏移的计算效率。




表1 高斯束偏移与二阶广义屏偏移有关参数
4 应用效果分析
我们将高斯束叠前深度偏移算法应用于西亚某地区的实际资料成像处理。研究区地质条件复杂,速度横向变化剧烈,存在高陡构造,而且原始资料品质差,经过前期处理的偏移输入道集如图9a所示。由图9a可见,该区地震资料信噪比较低,尤其是在中深层,有效信号被噪声淹没。图9b为建立的深度域速度模型。图10a和图10b分别给出了对研究区地震资料进行克希霍夫偏移和高斯束偏移的结果;图11a和图11b分别给出了CMP50和CMP250处高斯束偏移生成的角度域共成像点道集。对比图10a和图10b可见,高斯束偏移结果信噪比较高,同相轴连续性更好,特别是在陡倾角区域(图中椭圆区域),高斯束偏移方法实现了对高陡构造的优质成像;在深层由于输入道集信噪比低,克希霍夫方法抗噪能力相对较弱,成像效果较差,而高斯束偏移剖面中深层信噪比较高,同相轴连续性较好。
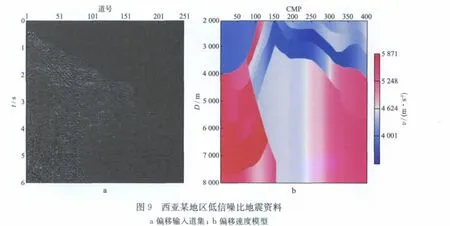
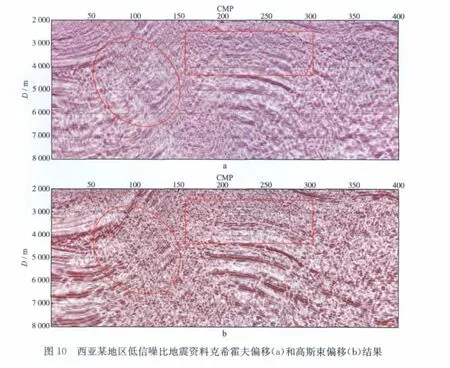
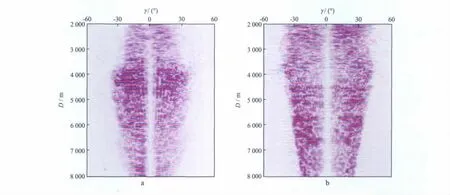
图11 角度域共成像点道集
5 结束语
高斯束偏移方法保留了射线方法灵活高效、无倾角限制的优势,同时克服了焦散、阴影区、多值走时等问题;基于射线中心坐标系的动力学射线追踪得到的慢度信息可直接用于计算共成像点角度道集。复杂模型和实际数据的测试结果验证了高斯束偏移方法在陡倾角构造、低信噪比资料成像方面的优势。
本研究仅限于各向同性介质的构造成像,在振幅保持以及各向异性高斯束偏移方面有待更深入的研究。
[1]Virgilio M,Simone R,Daniele C.Gaussian beam migration:prestack,common-shot,TTI,true amplitude in angular domain[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,2236-2239
[2]Cockshott I.Specular beam migration—a low cost 3D prestack depth migration[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006,2634-2637
[3]Gao F,Zhang P,Dirks V.Fast beam migration—a step toward interactive imageing[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,2470-2474
[4]ˇCervenýV,Popov M M,Pˇsenˇcík I.Computation of wave fields in inhomogeneous media—gaussian beam approach[J].Geophysical Journal Royal Astronomical Society,1982,70:109-128
[5]ˇCervenýV,Pˇsenˇcík I.Gaussian beams in elastic 2-D laterally varying layered structures[J].Geophysical Journal Royal Astronomical Society,1984,78:65-91
[6]Costa C A,Raz S,Kosloff D.Gaussian beam migration[J].Expanded Abstracts of 59thAnnual Internat SEG Mtg,1989,1169-1171
[7]Hill N R.Gaussian beam migration[J].Geophysics,1990,55(11):1416-1428
[8]Hale D.Migration by the Kirchhoff,slant stack,and Gaussian beam methods[R].Colorado:CWP Annual Project Review Meeting,1992
[9]Hale D.Computational aspects of Gaussian beam migration[R].Colorado:CWP Annual Project Review Meeting,1992
[10]Hill N R.Prestack Gaussian beam depth migration[J].Geophysics,2001,66(4):1240-1250
[11]Gray S H.Gaussian beam migration of common-shot records[J].Geophysics,2005,70(4):S71-S77
[12]Claerbout J F.Imaging the earth's interior[M].Oxford:Blackwell Scientific Publication,1985:376-378
[13]郭朝斌,李振春,岳玉波.高斯束成像技术及其应用[J].石油物探,2011,50(1):38-44,58 Guo C B,Li Z C,Yue Y B.Gaussian beam migration and its application[J].Geophysical Prospecting for Petroleum,2011,50(1):38-44,58
[14]李振春,岳玉波,郭朝斌,等.高斯波束共角度保幅深度偏移[J].石油地球物理勘探,2010,45(3):360-365 Li Z C,Yue Y B,Guo C B,et al.Gaussian beam common angle preserved-amplitude migration[J].Oil Geophysical Prospecting,2010,45(3):360-365
[15]ˇCervený V.Seismic ray theory[M].New York:Cambridge University Press,2001:234-400

