基于MPI和CUDA的转换波Kirchhoff叠前时间偏移并行计算
喻 勤,张少华,孔选林
(1.中国石油化工股份有限公司西南油气分公司勘探开发研究院德阳分院,四川德阳 618000;2.中国石油化工股份有限公司多波地震技术重点实验室,四川德阳 618000;3.东方地球物理公司科技信息处,河北涿州 072750)
转换波Kirchhoff叠前时间偏移是转换波地震数据处理中的一项关键技术,可实现全空间三维转换波资料的准确成像[1]。但转换波勘探数据量巨大,进行叠前偏移处理异常耗时。为了提高生产效率,目前大多数偏移算法采用大规模CPU 集群进行计算,但因集群设备存在着成本高、功耗大、占用空间大以及维护成本高等缺点,其发展空间受到限制。近几年,应用GPU 高性能计算进行地震偏移已成为一个新兴的研究热点,国内外很多地球物理公司都开展了基于GPU 的偏移算法研究[2-5],使叠前时间偏移、叠前深度偏移、单程波波动方程偏移、逆时偏移等性能得到数十倍的提升。我们在Linux环境下,利用MPICH2.1,CUDA toolkit4.2,Eclipse等工具,实现了基于MPI和CUDA 的转换波Kirchhoff叠前时间偏移并行算法。
1 转换波Kirchhoff叠前时间偏移原理
在转换波地震数据处理中,由于下行P 波和上行S波的路径不对称,需要做共转换点(CCP)[6]选排,因此,转换波资料处理流程一般为:抽CCP道集,速度分析,NMO,DMO,叠加和叠后偏移等。但因为CCP 面元化不易确定转换点真实位置,DMO 不能适应层间速度剧烈变化和大陡倾角情况,所以需要进行转换波叠前时间偏移。该技术不需要抽取CCP道集和DMO 处理就能实现全空间三维转换波资料的准确成像。
根据各向异性双平方根方程,叠前时间偏移方程[7-8]可以写成
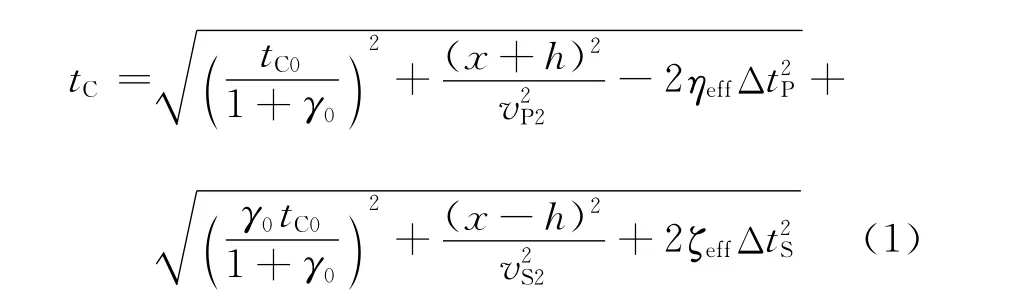
式中:tC为散射波旅行时;h是半源检偏移距;x为炮检距;ηeff,ζeff,γ0为各向异性参数;ΔtP是炮点到成像点的下行P波走时;ΔtS是成像点到检波器的上行S波走时;vP2是下行P波速度;vS2是下行S波速度。由于从实际转换波数据中很难获得vS2,在各向异性速度分析时也得不到vP2,因此这两个参量利用等效的转换波速度vC2转换得到。
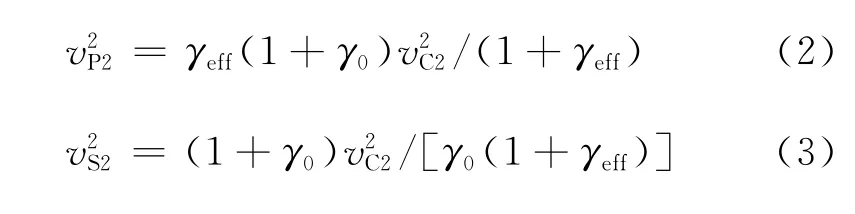
图1为转换波成像示意图,转换波叠前时间偏移算法是计算出炮点到成像点的下行P 波走时tP,成像点到检波器的上行S波走时tS,依据散射波旅行时公式(1),将上、下行波走时之和tPS上的能量累加到成像点处。转换波Kirchhoff叠前时间偏移能将任何道集形式的输入转换成共成像点(CIP)道集。任意一个检波点上接收的能量都可以依据炮检点间的空间关系和各向异性旅行时方程分配到空间所有可能的成像位置,而所有炮检对的能量都可以依据方程给出的射线路径累加到图1中散射点(成像点)的成像位置,从而使转换波在三维空间任何位置准确成像。
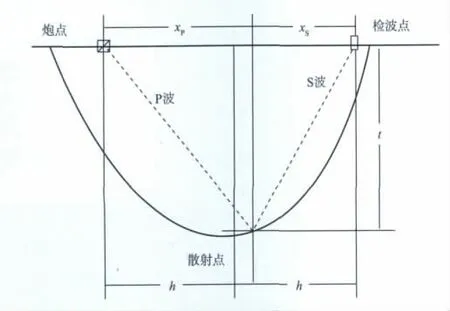
图1 转换波成像原理
转换波叠前时间偏移从理论上规避了输入数据零炮检距的假设,从而避免了NMO 校正叠加产生的畸变,比叠后时间偏移能保存更多的叠前信息。叠前偏移后的叠加是共反射点的叠加,依据的模型是任意非水平层状介质,因此比叠后偏移成像在空间位置上更准确。此外,叠前时间偏移采用均方根速度场,可以逐点进行速度分析,成像精度较高,偏移速度较快,并可以提高AVO分析精度[9]。
2 基于MPI和CUDA 的算法实现
GPU 图形处理器[10-13]是专门负责图形渲染的核心处理器,内部有上百个计算核心。CUDA 是Nvidia公司开发的一种SIMT 并行编程模型,用于开发高度并行的线程级程序。MPI[14-15]是一种基于消息传递并行编程模型的标准规范,从程序设计的角度理解是一个并行函数库,其具体实现包括MPICH,OPEN MPI,LAM,IBM MPL 等多个版本,最常用和稳定的是MPICH 和OPENMPI。MPI是目前超大规模并行计算应用最广、效率最高的并行编程模型,几乎被所有并行环境(共享和分布式存储并行机、集群系统等)和多进程操作系统(UNIX,Linux,Windows NT)所支持,基于MPI开发的应用程序具有可移植性、适用性、易用性、可扩展性强和性能高等优点。通过MPI可以方便地连接现有计算机,进行高性能集群计算。
MPI与CUDA 的最大优势均在于并行计算,但是MPI面向的是主处理器CPU 进程间的并行,属于粗粒度级的并行,而CUDA 的并行是协处理器GPU 线程间的并行,属于细粒度级的并行。要实现基于MPI和CUDA 的并行算法,需要对计算任务进行划分,偏向管理控制的部分采用进程间的并行计算,计算密度大的部分采用线程间的并行计算。通过主处理器CPU 和协处理器GPU 结合,可以最大限度地发挥计算机的处理能力。
基于MPI和CUDA 的Kirchhoff叠前时间偏移并行算法设计主要包括以下几个方面。
1)从硬件系统上考虑,采取一个CPU 绑定一个GPU 的方式,这样可以形成最小计算粒度的节点,比较灵活地进行数值计算,保证其单独享有L2和L3缓存,避免多核CPU 产生的数据竞争问题,减少资源需求,从而降低内存负载,保持CPU 到显存PCI-E信道、CPU 到主存以及主存到硬盘总线的高带宽。
2)CPU 进程间的通信通过MPI来完成,每个CPU 进程绑定一个GPU。MPI主要用于完成均衡的任务分割,完成偏移过程所需相关参数的计算以及对各节点分发数据、管理控制各节点GPU 的计算流程等任务。每个节点的GPU 主要用于实际偏移计算,偏移计算所需的参数可以通过MPI分发到各个GPU 节点上。对速度数据建立了一个数据表,供各个GPU 快速查询使用,通过叠加各个CPU 节点的计算结果,得出最终偏移剖面。偏移计算流程见图2所示。
3)由于偏移本质上是一个信号能量再分配的过程,即将接收信号的能量按照一定的关系分配到地层的各个反射点上,最终偏移后输出的地震道和每一道检波器所采集的数据都有关系,但相互之间是独立的。因此可以把偏移过程简化为若干个独立的、不相关的子问题,转化为GPU 轻量级多线程应用。
4)从GPU 硬件特性考虑,采取了多道输入和多道输出相结合的方式,一次读取多道数据进行偏移处理,得到整个成像空间的成像点数据再进行输出。该方式需要相对较少的输入数据并加以重复利用,大幅度减少了主存和显存之间的拷贝次数及拷贝时间,实现了数据的高吞吐并行计算。
5)设计中还需要考虑GPU 算法的均衡性,对于每个GPU 来说,偏移计算过程需要分块(block)计算,每个块中的计算需要线程同步,最为平均的计算量可以减少同步等待的时间。线程数量过多会导致线程同步时间变长,也会导致计算过程中寄存器数量不足以及进出堆栈带来的损耗;线程数量过小,会导致块数量增多,块之间切换开销相对较大。因此,在算法设计中,需要根据偏移计算需要的寄存器变量及计算过程的复杂性合理分配每个块中的线程数量。
6)设计CUDA 偏移算法关键的一点,是如何在偏移计算过程中利用共用存储器,在不发生存储体冲突时,访问延迟与寄存器相同。在不同的块之间,共用存储器是动态分配的。在同一个块内,共用存储器是进行线程间低延迟数据通信的唯一手段。将偏移过程中每个块内的线程都需要的变量放入共用存储器进行访问,例如最后的偏移能量累积叠加利用共用存储器进行,保证了访问全局内存的次数最少,避免了采用全局内存的不合并访问而造成的效率低问题,从而提高计算效率。
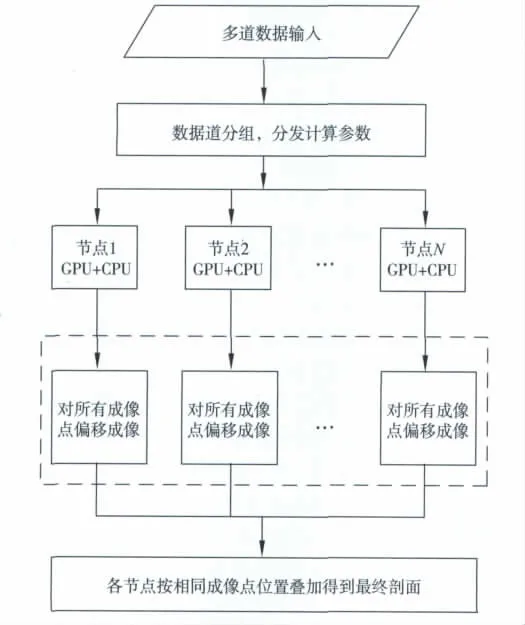
图2 基于MPI和CUDA 的偏移计算流程
3 算法测试与效果分析
为测试基于MPI和CUDA 的Kirchhoff叠前时间偏移并行算法的性能,我们在Linux操作系统下实现了该算法。测试平台为DELL 的6节点小型集群,集群中有2 个Tesla M2070 GPU 节点。测试环境配置如表1所示,测试数据为川西某区块转换波数据。选取其中4组进行测试。
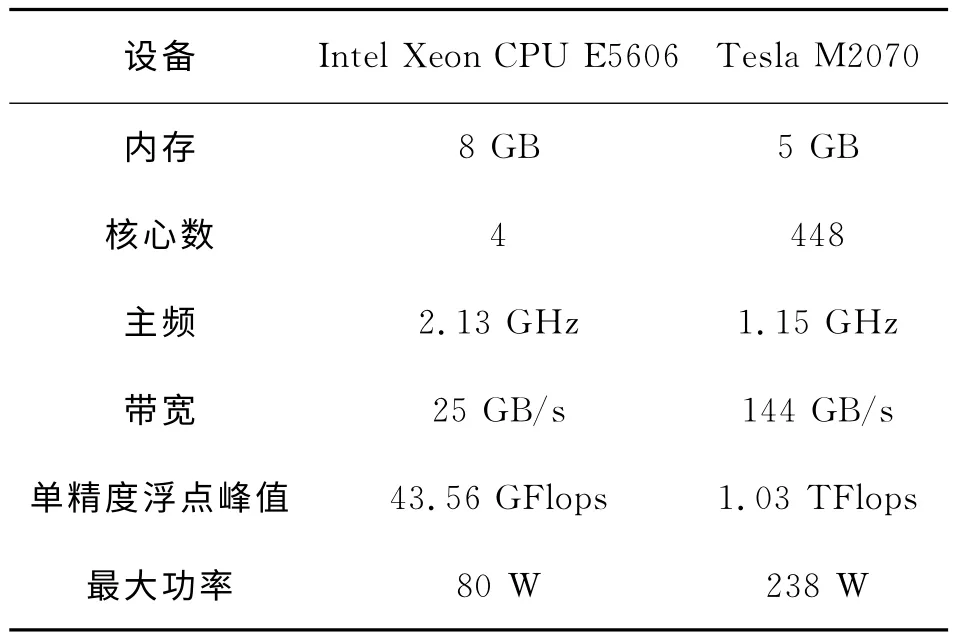
表1 测试环境
分别利用Intel Xeon CPU E5606单核,Tesla M2070GPU单卡以及MPICH2 和CUDA4.2 在集群上的2个GPU 节点对4组数据进行了测试。以往采取的计算热点部分比较忽略了如CPU 到GPU 数据拷贝传输过程、GPU 到CPU 的输出过程以及其它一些会耗时的过程,虽然计算部分加速比非常高,但是整个计算任务的加速比低得多。为了获得更客观的计算效率,选取相同的计算量,即给出相同的计算任务,统计其以相同的偏移算法、不同的计算方式来完成所需要的总的时间(表2),最终获得GPU 计算加速比,即串行执行时间/并行执行时间(表3)。这个加速比真正反映了一个计算任务的加速比。
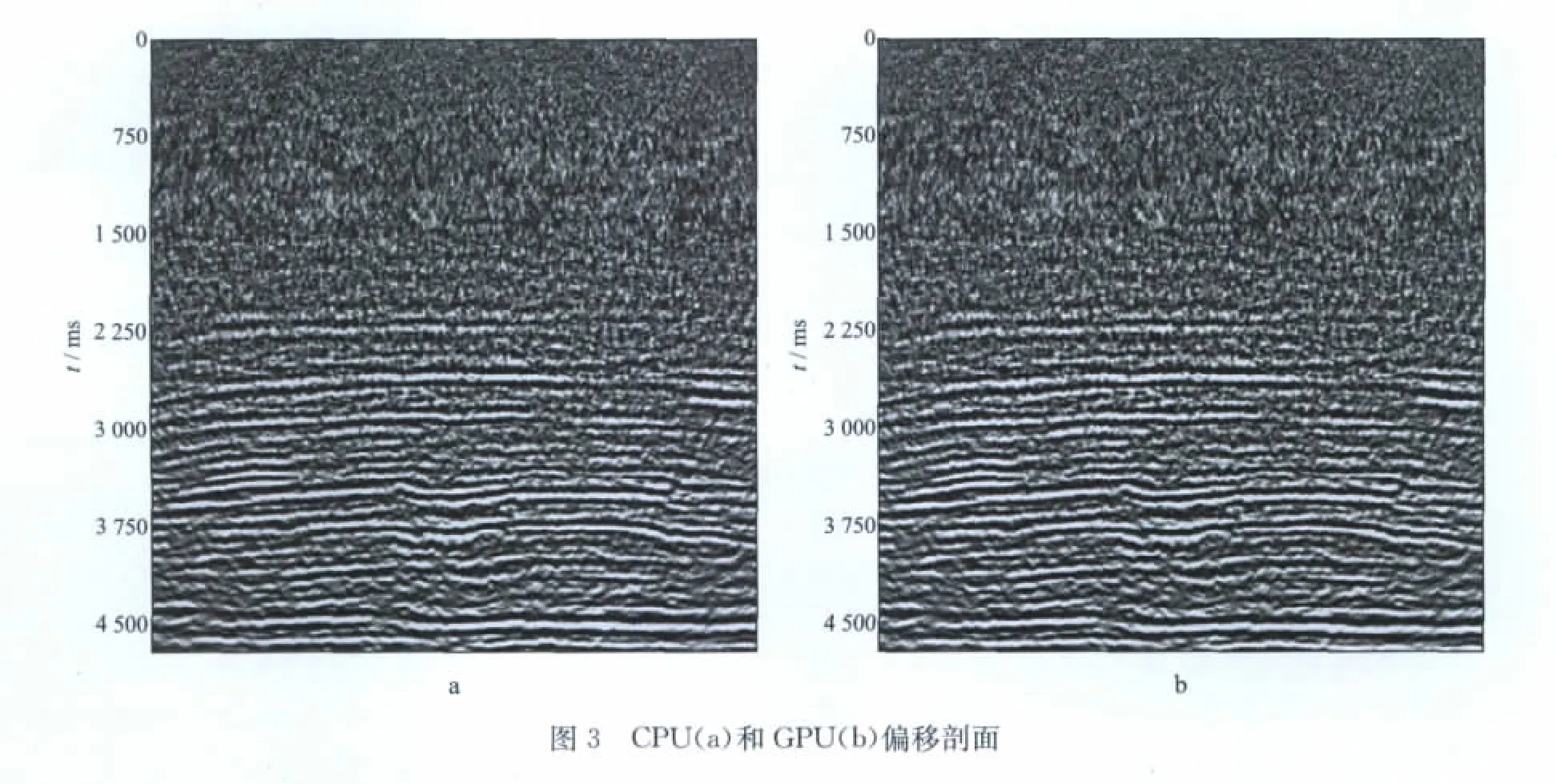
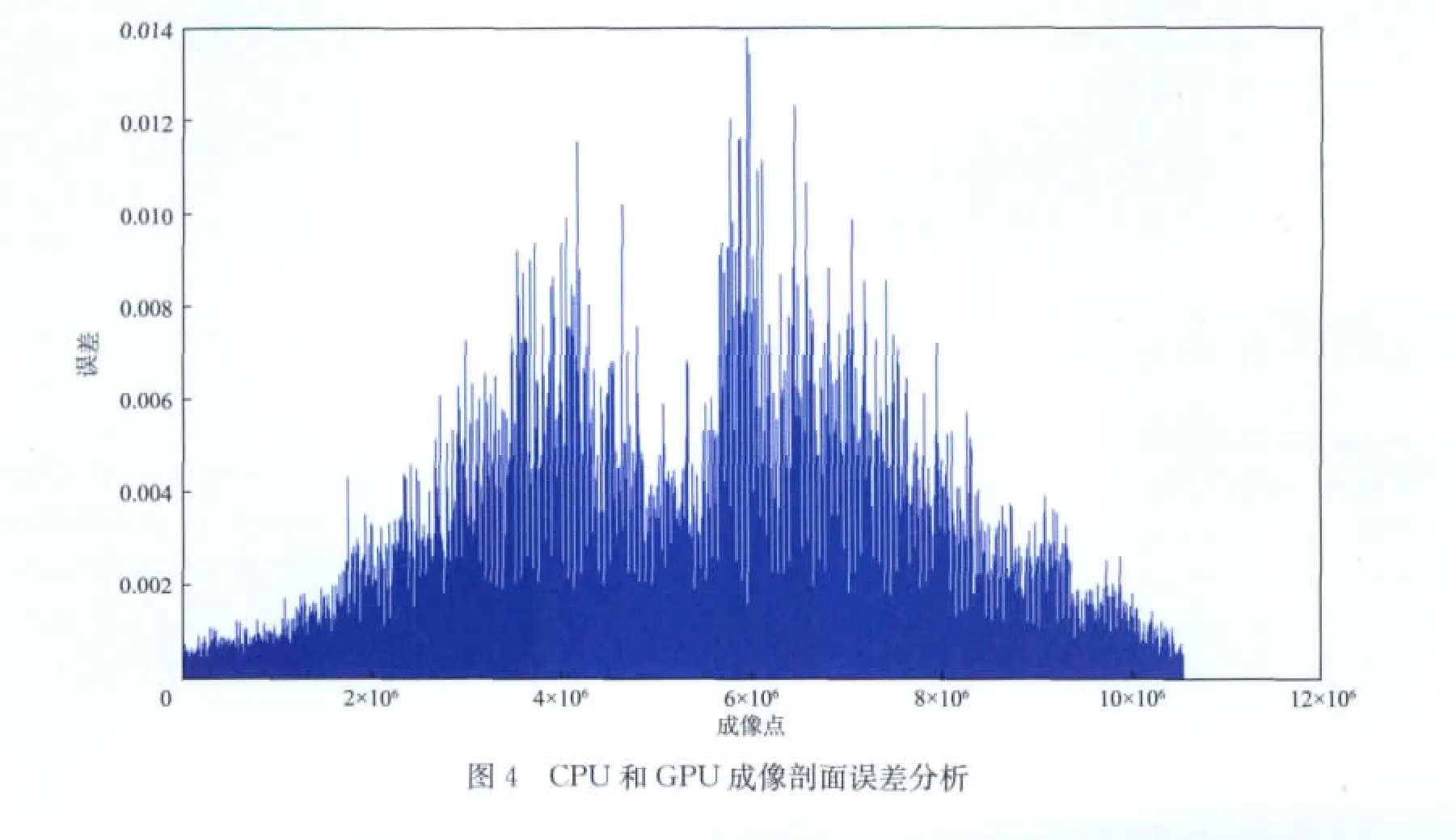
从以上结果可以看出,基于CUDA 的偏移计算效率得到大幅度提升,即使在小数据量任务未能充分利用GPU 的情况下,计算效率也有大幅度提升。在数据量充分的情况下,GPU 单卡的速度比是CPU 单核的近200倍,利用MPI和GPU 的2个节点的计算速度比是CPU 单核的近400倍。针对4.76GB的测试数据,分别利用单核CPU,MPI和GPU 进行偏移计算,得到的剖面如图3 所示。将两个剖面所对应的点进行数值误差分析,结果如图4所示,幅度误差被控制在0.01的数量级,表明GPU 的计算精度对实际资料的成像结果基本没有产生影响。

表2 测试计算时间 ms

表3 测试计算加速比
4 结束语
本文研究给出了基于MPI和CUDA 的转换波Kirchhoff叠前时间偏移并行算法,测试分析结果表明:MPI和GPU(2 个节点)的计算速度是CPU(单核)的近400 倍,大幅度提高了转换波Kirchhoff叠前时间偏移的计算效率,降低了计算成本。
基于MPI和GPU 的高性能计算技术有利于实现叠前时间偏移多次迭代,获得合理匹配的速度模型,使得提高转换波资料处理品质成为可能。但是,GPU 偏移成像剖面还存在假频现象,分辨率也有所降低,因此需要从反假频和提高分辨率两个方面对偏移算法进一步进行深入研究。
[1]马昭军,唐建明.叠前时间偏移在三维转换波资料处理中的应用[J].石油物探,2007,46(2):174-180 Ma Z J,Tang J M.The application of prestack time migration in 3Dconverted-wave data processing[J].Geophysical Prospecting for Petroleum,2007,46(2):174-180
[2]张兵,赵改善,黄俊,等.地震叠前深度偏移在CUDA 平台上的实现[J].勘探地球物理进展,2008,31(6):427-432 Zhang B,Zhao G S,Huang J.Implement prestack depth migration on CUDA platform[J].Progress in Exploration Geophysics,2008,31(6):427-432
[3]刘国峰,刘洪,王秀闽,等.Kirchhoff积分叠前时间偏移的两种走时计算及并行算法[J].地球物理学进展,2009,24(1):131-136 Liu G F,Liu H,Wang X M,et al.Two kinds of traveling time computation and parallel computing methods of Kirchhoff migration[J].Progress in Geophysics,2009,24(1):131-136
[4]李肯立,彭俊杰,周仕勇.基于CUDA 的Kirchhoff叠前时间偏移算法设计与实现[J].计算机应用研究,2009,26(12):4474-4477 Li K L,Peng J J,Zhou S Y.Implement Kirchhoff prestack time migration algorithm on CUDA architecture[J].Application Research of Computers,2009,26(12):4474-4477
[5]刘国峰,刘钦,李博,等.油气勘探地震资料处理GPU/CPU 协同 并行计算[J].地 球 物理学进展,2009,24(5):1671-1678 Liu G F,Liu Q,Li B,et al.GPU/CPU co-processing parallel computation for seismic data processing in oil and gas exploration[J].Progress in Geophysical(in Chinese),2009,24(5):1671-1678
[6]Li X Y.Converted-wave moveout analysis revisited:the search for a standard approach[J].Expanded Abstracts of 73rdAnnual Internat SEG Mtg,2003,805-808
[7]Li X Y,Dai H C,Mancini F.Converted-wave imaging in anisotropic media:theory and case studies[R].Edinburgh:Edinburgh Anisotropy Project,2006
[8]Li X Y,Yuan J X.Converted wave traveltime equations in layered anisortropic media:an overview[R].Edinburgh:EAP Annual Research Report,2001:3-32
[9]Dai H C,Li X Y,Conway P.3Dpre-stack Kichhoff time migration of PS-waves and migration velocity model building[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,1115-1118
[10]John D O.A surey of general-purpose computation on graphics hardware,eurographics [EB/OL].(2005-06-23)[2012-03-15]http://www.realworldtech.com/page.cfm?ArticleID=RWT0908
[11]Nvidia.Nvidia CUDA compute unified device architecture programming guide version4.0[EB/OL].[2011-12-9]http://developer.download.Nvidia.com/compute/cuda/4_0/docs/CudaReferenceManual_4.0.pdf
[12]张舒,褚艳丽,赵开勇,等.GPU 高性能计算之CUDA[M].北京:中国水利电力出版社,2009:25-30 Zhang S,Chu Y L,Zhao K Y,et al.GPU high performance computing on CUDA[M].Beijing:China Publishing Company of Water Conservancy and Electric Power,2009:25-30
[13]Budruk R,Anderson D,Shanley T.PCI express system architecture[EB/OL].[2012-03-15]http://www.docin.com/touch/detail.do?id=501507982
[14]都志辉.高性能计算之并行编程技术-MPI并行程序设 计[EB/OL].(2007-10-9)[2012-03-15]http://wenku.baidu.com/view/00bacc204b35eefdc8d33375.html Du Z H.The parallel programme technolegy of high performance computing-MPI parallel programming[EB/OL].(2007-10-9)[2012-03-16]http://wenku.baidu.com/view/00bacc204b35eefdc8d33375.html
[15]John D O,Mike H,David L,et al.GPU computing[J].Proceedings of the IEEE,2008,96(5):879-897

