引入曝光因子的最大信息量动态分层法

詹沛达 王立君 杨卫敏

1 引言

由于社会的进步和知识经济的不断发展，考试作为衡量能力的一种手段已经深入到社会的各个方面。随着科学技术的进步，考试的方式也在发生着革命性的变化：从传统的纸笔考试到计算机辅助考试，到具有自适应能力的计算机化自适应测验（Computerized Adaptive Testing，CAT）考试，其实现方法由单机形式逐步向不受时间、地点的网络考试发展。CAT是基于项目反应理论（Item Response Theory，IRT）、计算机技术和现代教育技术的一种测验形式，它根据被试的在已作答项目上的表现自适应地从题库或剩余题库中选择测验项目施测。与传统纸笔测验相比，CAT的主要优点在于使用较少的题目而达到对被试能力值更精准的估计（Weiss，1982）。

CAT包括六个基本组成部分：采用的项目反映模式、题库、初始项目的选择、参数估计方法、选题策略和测验终止规则（Weiss&Kingsbury，1984）。其中，选题策略作为CAT的重要环节之一，它的好坏与测验的信、效度，测验安全性以及测量准确性直接相关。就CAT中最为经典的最大Fisher信息量（Maximum Fisher Information，MFI，Lord，1977）策略而言，虽然其测验效率高、能力估计准确，但由于没有考虑题目的曝光控制问题，会导致题目调用很不均匀，影响了题库的使用率，因此MFI很少单独应用在实际的自适应测验系统中。对此，前人也提出了一系列改进方法，主要包括S-H法（Sympson-Hetter method，S-H，Sympson&Hetter，1985）、渐进法（Progressive Method，PG，Revuelta& Ponsoda，1998）、比例法（Proportional Method，PP，Segall，2004）、a分 层 法（a-STRatified method，a-STR，Chang&Ying，1999）、b模块化的a分层法（BAS，Chang，Qian，&Ying，2001）等。

其中，a-STR作为较为独特且运用较广的一种选题策略可以有效控制题目曝光率以提高测验的安全性。针对a-STR存在的些许不足，前人也对其进行了一系列的改进，但仍有一些不足没有得到改进，如（1）测验是固定长度的，而通常情况下自适应测验都是不定长的；（2）需要人为在测验前确定分层数量，且分层数量固定不变，也没有失效时间。鉴于这两个问题，鹿士义和张坚（2011）提出了动态a分层方法（Dynamic a-Srtatified Method，DAS）。在DAS中随着测验的进行分层数逐渐减少，直到减到一个分层后方法失效，自动退化为如最大信息量法进行选题，其分层数减少的计算方法如下：

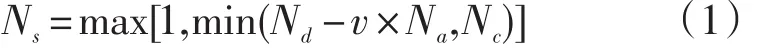
式中，Ns为当前分层数，Nd为初始分层数量（原文为策略失效时的有效题目数），Na为已施测的题目数，Nc为候选的题目数，v为速度因子。鹿士义等（2011）认为，Ns会随着Na的增加而减少，这也使得每层中的题数逐渐增加，从而候选的区分度较高的题目也逐渐增加，这样也达到了区分度较高的题目被留在测验后期阶段施测的目的，与a-STR在效果上差不多。此外，DAS的整个测验阶段都在同一个分层中进行，因此无须设定测验长度，这适应了自适应测验的要求。

与a-STR不同，DAS不要求固定的阶段选题策略，因此提供了一种有待验证的、较好的思路：在测验前期（分层法失效前）保留分层法的特色（提高区分度较小的题目的曝光率），又能在能力估计较精准的测验后期（分层法失效后）使用效率更高的方法来进一步提高测验的效率、减少测验的长度。但通过分析鹿士义等（2011）文章中的结果，我们认为DAS在测验效率、曝光率控制方面的表现均不突出，此外，其文中也没有涉及动态分层法和非动态分层法在不定长测验中的对比研究。因此本文针对DAS的上述问题，通过结合目前已有的研究提出了新的方法，以期对DAS进行更好地优化，同时探究DAS不要求固定阶段选题策略的思路是否有较好的表现。本文所结合的研究有：（1）曝光因子（exposure-control factor，ecf，程小杨，丁树良，严深海，朱隆尹，2011）；（2）最大信息量分层法（Maximum Information Stratification Method，MIS，Barrada，Mazyele，&Olea，2006）。此外，将动态分层法和非动态分层法在不定长测验中进行了对比。

2 引入曝光因子的最大信息量动态分层法

2.1 关于3PLM模型的简介

伯恩鲍姆（A.Birnbaum）给出了如下的三参数Logistic模型（3PLM）（漆书青，戴海崎，丁树良，2002）：

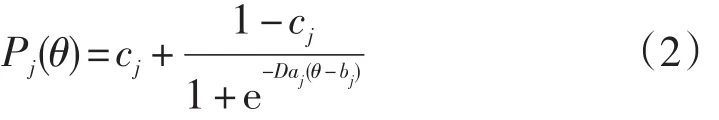
式中，θ为被试能力，D为常数（一般取值1.7），aj、bj、cj分别表示第 j个项目的区分度、难度和猜测度，Pj（θ）表示能力为θ的被试在第j个项目上正确作答的概率。

2.2 关于曝光因子和最大信息量分层策略的简介

2.2.1 关于曝光因子（ecf）的简介

针对CAT中使用MFI法选题会导致项目的使用不均匀，影响考试安全的缺点，程小杨等（2011）在MFI的基础上引入一个项目j的控制曝光因子ecf：

式中，mj表示项目j被前m-1个考生调用的次数，m表示前m-1个考生调用题库中所有项目的平均次数，即为题库项目总数。ec（fj）会随着mj的增大而增大。更具体的内容可参见程小杨等（2011）的文章。

2.2.2 关于最大信息量分层策略（MIS）的简介

Barrada，Mazyele和 Olea（2006）在分析 a-STR和BAS后，发现它们只虑了两个题目参数：题目区分度a和题目难度b，而对于3PLM特有的题目猜测度c参数并没有考虑在内。由于在3PLM中，将题库按照区分度a排序与按题目最大信息量Ijmax排序得到的结果并不一致，与最大信息量Ijmax对应的能力值θjmax也不会与题目难度b相等。因此，在3PLM中a-STR策略和BAS策略并不会达到应有的效果（詹沛达，王立君，2012）。为了将题目猜测度c参数引入到分层法中，Barrada等人（2006）对a-STR和BAS进行了两处重要的修改：一是使用题目最大信息量Ijmax代替区分度a；二是用题目信息函数达到最大值时对应的能力值θjmax代替难度b。

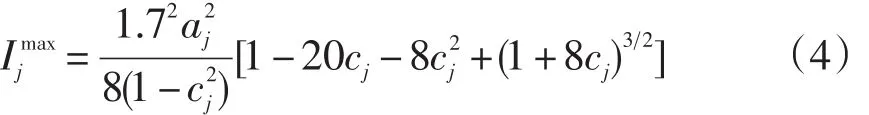
式中，aj是题目 j的区分度参数，cj是题目 j的猜测度参数。

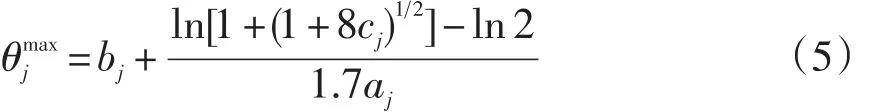
MIS的操作步骤与a-STR类似，具体可参看Barrada等人（2006）、詹沛达和王立君（2012）的文章。

2.3 新的选题策略

为了能改善DAS在测验效率和曝光率控制方面的变现，依次将ecf和MIS引入DAS中，以期对DAS进行更好地优化。

2.3.1 引入曝光因子的动态a分层法（DAS-ecf）

受程小杨等（2011）提出引入曝光因子的按a分层法的启发，对DAS加入ecf以形成新的选题策略，DAS-ecf，被试选择项目j满足以下公式；

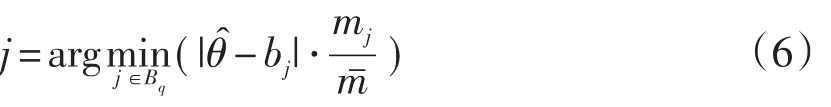
分析公式（6），当mj越大，ecf（j）也越大，即该项目被调用的次数越多，则它在后面被选中的概率越小。如此达到更均匀地调用项目的目的。当然在实际施测过程中，为避免mj为0的情况，我们用mj+ε（ε为足够小的正数）来代替mj，用m+ε代替m（程小杨等，2011）。

2.3.2 引入曝光因子的最大信息量动态分层法（DMIS-ecf）

在考虑到DAS没有考虑到c参数的同时，也希望能将DAS和MIS的优点进行融合。首先，对MIS进行修改，形成类似于DAS的DMIS，即最大信息量动态分层法。之后，与DAS-ecf一样，将ecf引入DMIS以形成DMIS-ecf，被试选择项目j满足以下公式：

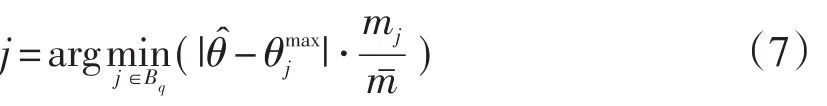
与DAS-ecf中一样，随着项目被调用的次数的增加，其在后期被选中的概率减小。此外，同样用mj+ε（ε为足够小的正数）来代替mj，m+ε代替 m。

3 CAT的模拟过程

本研究分为两个实验，且实验一与实验二的施测过程、评价指标均相同。

3.1 实验一：多种选题策略的对比

3.1.1 被试及题库模拟

当被试能力真值和题目参数真值均未知时，要评价新的CAT选题策略对能力估计的影响需用Monte Carlo模拟实验。本研究基于3PLM，采用Monte Carlo模拟方法，文中的模拟数据（包括题目参数、被试能力参数）和CAT的施测程序均采用R version 2.15.0（64-bit）编写运行。模拟数据结构（陈平，丁树良，林海菁，周婕，2006）如下：

（1）产生一批题目参数，各参数分布情况分4种情况：

①区分度参数a服从对数正态分布，难度参数b服从标准正态分布，记为lna～N（0，1），b～N（0，1）；②ln a～N（0，1），难度参数b服从均匀分布，记为b～U（3，3）；③a～U（0.2，2.5），b～N（0，1）；④a～U（0.2，2.5），b～U（3，3）。对于以上四种题库分布，猜测概率参数c均服从α为5和β为17的贝塔分布，记为c～Beta（5，17），且a∈［0.2，2.5］，b∈［-3，3］。每种情况均有800个项目。

（2）模拟的被试数量为1000人，能力参数θ服从标准正态分布，记为θ～N（0，1）。

3.1.2 实验设计

在实验一中，为方便与前人的研究进行对比，本文将MIS和a-STR的阶段终止规则进行修改（见下文），使其适用于不定长CAT，并对其引入曝光因子形成MIS-ecf和a-STR-ecf。最后，通过Monte Carlo模拟方法，基于3.1.1中的4种题目参数分布情况对以下8种方法进行对比研究：

（1）a分层法（a-STR）；

（2）动态a分层法（DAS）；

（3）最大信息量分层法（MIS）；

（4）最大信息量动态分层法（DMIS）；

（5）引入曝光因子的a分层法（a-STR-ecf）；

（6）引入曝光因子的MIS分层法（MIS-ecf）；

（7）引入曝光因子的动态a分层法（DAS-ecf）；

（8）引入曝光因子的最大信息量动态分层法（DMIS-ecf）。

实验一为4×8交叉研究，共32个实验，每个实验均对1000名被试进行20次CAT模拟全过程。研究采用不定长CAT测验，当测验总信息量达到16（即测验标准误为0.25）时测验停止。除动态分层法外，其余选题策略的分层数均分为4，每层200题，且在不定长CAT中，其余选题策略均需要知道阶段终止规则以便进入下一阶段或下一层选题。本文中是根据信息量的大小作为阶段终止规则，各阶段（层）累积测验信息量（程小杨等，2011；陈平等，2006；戴海琦，陈德枝，丁树良，邓太萍，2006）的大小满足如下公式：

如前所述，I总设定为16，总分层数T为4，k表示当前所在层数或阶段数。

此外，对于所有的动态分层法，需要在测验进行之前设定好初始分层数Nd和加速因子v。为了与其他分层策略第一层的题数保持一致，将Nd设定为4。且鹿士义等（2011）指出最好的速度因子是0.2，因此本文将所有动态分层法的v都设定为0.2。

3.2 实验二：不同阶段选题策略的DMIS-ecf对比

与DAS一样，DMIS-ecf也不要求固定的阶段选题策略。为探究不同阶段选题策略对DMIS-ecf的影响，我们在实验二中设定了三种不同阶段选题策略的方法：（1）全程采用难度匹配法（即实验一中的DMIS-ecf），将其定义为DMIS-ecf1；（2）分层策略失效前采用BM法且分层策略失效后采用MFI法，将其定义为DMIS-ecf2；（3）全程采用MFI法，将其定义为DMIS-ecf3。

同样，通过Monte Carlo模拟方法，基于3.1.1中的4种题目参数分布情况对这3种方法进行对比研究。

3.3 施测过程

施测过程分为初始探测阶段和正式测验阶段。在初始探测阶段，我们采用从剩余题库中随机抽取试题给被试作答，直到作答题数不少于3且作答总分既不为0分也不为满分时，结束初始探测阶段。根据被试的作答得分向量，估计能力初值，进入正式测验阶段。在正式测验阶段，针对不同的选题策略，从剩余题库中调用与被试当前能力值匹配的项目。被试作答完成后，根据作答得分向量估计被试当前能力值。直到测验总信息量达到16时，测验结束。

测验过程中，通过以下方法模拟被试得分（陈平等，2006）：根据被试能力真值θ和当前所选择的项目j的参数，由公式（1）计算被试在第j个项目上的答对概率Pj（θ），再产生一个随机数r（0≤r≤1），若r≤Pj（θ），则该被试在第j个项目上得1分，否则得0分。此外，假设被试能力的先验分布为标准正态分布，采用贝叶斯期望后验估计法（EAP）估计被试能力。

3.4 评价指标

选题策略的优劣直接关系到CAT的质量，当其他条件固定仅改变选题策略时，对CAT的评价实际上就是对选题策略的评价（陈平等，2006），故本文采用以下评价指标：

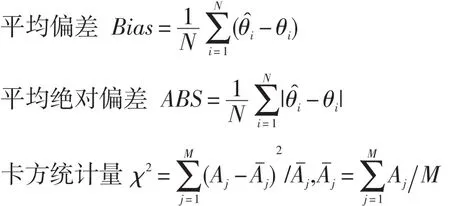
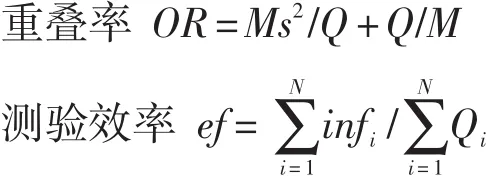
其中，N为被试总数；θi为被试能力真值；θ̂i为被试能力估计值；Q表示平均测验长度；Qi表示被试i的测验长度；M为题库大小；infi表示被试i的测验信息总量；Aj是第j题曝光率，其计算公式为Aj=第j题被使用的次数/N；s是题目曝光率的标准差。重叠率定义为任意两个随机选取的被试的重叠题目数的期望值除以考试的长度，对于大样本，测验重叠率近似值为OR。

以上5个指标中，前4个指标越小越好，ef指标越大越好。其中OR越小，表明该方法选题重叠率越低；ABS越小，说明估计的精度越高；Bias越小，则表明该方法越接近无偏；值越小说明曝光率越均匀；而ef越大，说明测验效率越高。为了更直观地反映测验总体效果，我们将这些指标进行统一量纲再加权求和（由于各选题策略的Bias指标本身很小，但其微弱的变化都会对统一量纲产生较大的影响，因此本文并未将Bias指标列入统一量纲中。此外，各指标的权重均设为1）。关于统一量纲具体操作方法见程小杨等（2011）、陈平等（2006）、戴海琦等（2006）的文章。

4 实验结果分析

4.1 实验一结果分析

从4个实验数据（表1-5）显示，几种选题策略的总体效果（平均统一量纲）从大到小的顺序为：MIS-ecf、 a-STR-ecf、 DMIS-ecf、 DAS-ecf、 MIS、a-STR、DAS、DMIS。引入ecf的方法在各个指标上均比未引入ecf的方法要优秀。动态分层法均比相应的非动态分层法表现要差，这也可能与动态分层法Nd和v的设定有关。引入c参数的M簇（以MIS为基础）策略总体上比A簇（以a-STR为基础）策略好，但差异很小。

表1 ln a～N（0，1），b～N（0，1），c～Beta（5，17）时的实验结果

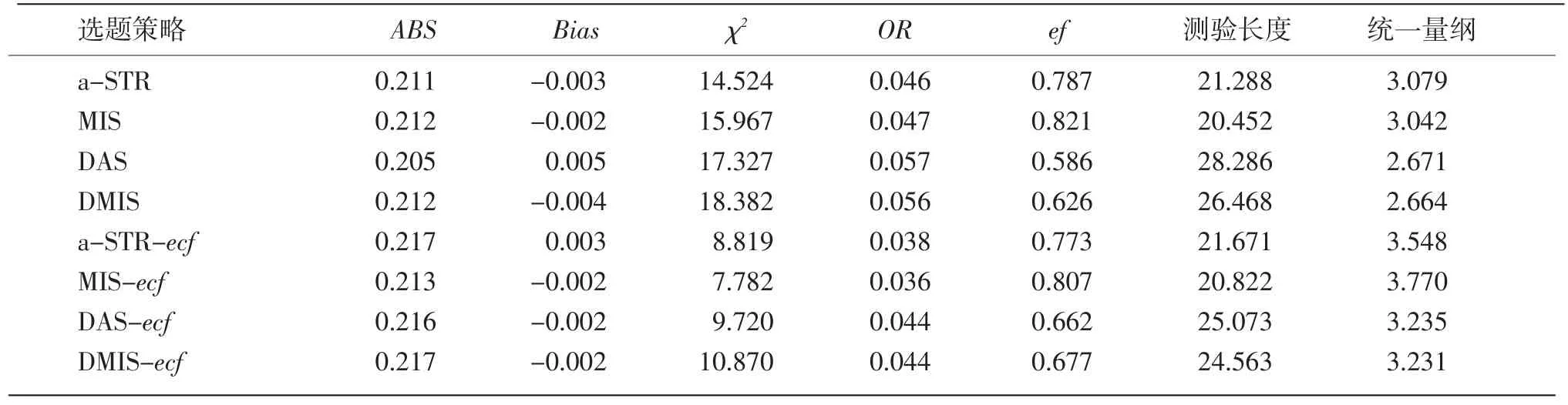
表2 ln a～N（0，1），b～U（-3，3），c～Beta（5，17）时的实验结果

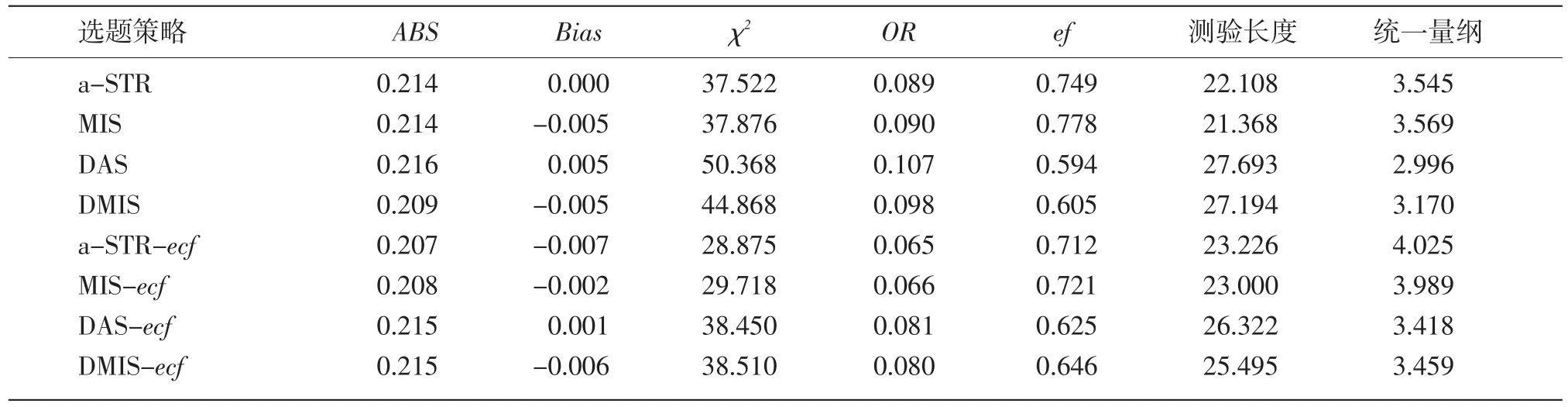
表3 a～N（0.2，2.5），b～N（0，1），c～Beta（5，17）时的实验结果

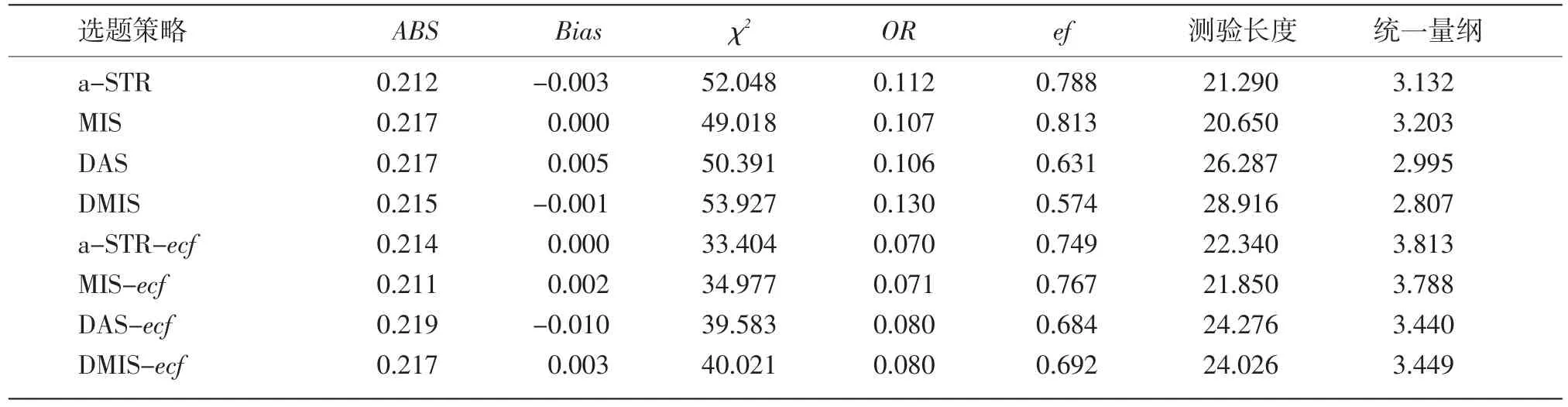
表4 a～U（0.2，2.5），b～U（-3，3），c～Beta（5，17）时的实验结果

表5 各阶段被试的平均测验长度

从题目参数分布情况对评价指标的影响看，参数a的改变对8种选题策略的影响较大，而参数b的改变的影响较小。事实上，在模拟实验中发现，选题策略的好坏还与题库有弱依赖关系。题库1和题库2中，MIS-ecf均优于a-STR-ecf，题库3和题库4中，MIS-ecf却劣于a-STR-ecf。但从总体上讲，选题策略在4种题目参数分布情况下的优劣顺序基本没有变化，这说明不同选题策略的优劣主要是其自身所固有的。

从ABS指标看，8种方法的测验精度基本一致。但有一点值得注意。

从Bias指标看，8种方法的Bias值均接近于0，因此它们基本都是无偏估计。

从ef指标看，当选题策略引入ecf后，由于其重复选择优质题目的概率下降，因此降低了该策略的效率。但动态分层法在引入ecf后，测验效率反而提高了。此外，M簇策略在ef指标上表现优于A簇策略。

从测验长度看，8种选题策略测验长度差异不大。

程小杨等（2011）曾指出：在引入曝光因子的选题策略中，引入ecf（j）来控制项目的选择，但由于题库中相应的优质项目（a值较大的项目）有限，而随着被试人数的增多，是否会使这些项目调用较频繁，从而这些项目的ecf（j）值会变大，而使较晚参加测验的被试只能选择a值小一些的项目导致测验长度增加，这一问题值得重视。为了考察是否存在此问题，我们分别记录了前期、中期、后期的被试的测验平均长度，具体见表5（题库分布为ln a～N（0，1），b～N（0，1），c～Beta（5，17）），从表5可知，对于前期、中期、后期的被试的测验平均长度相差并不大，并未引起较晚参加测验的被试的长度增加。其他三个题库下的实验结果也基本一致，因篇幅所限，故省略。

4.2 实验二结果分析

在实验二中探究了不同阶段选题策略对DMIS-ecf的影响，其实验结果如表6所示。单从测验效率指标（ef和测验长度）看，随着MFI法使用比例的增加确实会提高选题策略的效率，但从测验安全性指标（χ2和OR）看，MFI法使用比例的增加会导致安全性降低。从本研究的统一量纲看，DMIS-ecf1明显优于另外两个选题策略。虽然动态分层法不要求固定的阶段选题策略，但如果对测验没有特殊的要求（如题量和测验时间的限制），一般应全程采用难度匹配法作为阶段选题策略。

表6 不同阶段选题策略的DMIS-ecf的表现

5 讨论与结论

本文基于3PLM模型对DAS引入曝光因子ecf和最大信息量分层策略MIS，形成了几种新的选题策略，其中DMIS-ecf在各个评价指标上表现都良好，对DAS起到了明显的优化和提升，达到了本研究的目的。但从实验一的结果可以看出，MIS-ecf和a-STR-ecf在各评价指标上都要优DMIS-ecf，也即动态分层法在本研究中并未体现出其优势，这可能是动态分层发本身的缺陷，也可能和本研究对其初始参数的设定有关，这在今后的研究中还有待做进一步的确定。此外，对于DMIS-ecf，如果测验对题量和测验时间没有特殊要求，应全程采用难度匹配法作为阶段选题策略。

实验数据显示，M簇策略在测验效率上优于A簇策略，而在安全性劣于A簇策略，但总体差异很小，因此可针对不同的测验要求酌情选择。但从观念上讲，M簇策略考虑到了3PLM独有的猜测度c参数，这是值得提倡的。

引入曝光因子ecf的选题策略会使项目的调用更加均匀、曝光率指标明显降低，当然测验长度有一定增加，而能力估计准确性相差不大，这为提高CAT的安全性提供了一条途径（程小杨等，2011）。

当然本研究仍有一些问题值得今后做进一步的工作：（1）动态分层法初始参数的设定对DMIS-ecf的影响；（2）本研究中的MFI策略值比同类研究中值都大，且测验长度较短，这可能与模拟测验程序的编制水平或使用不同的模拟软件有关，今后还有待进一步提升和确定；（3）本文的重叠率指标（OR）采用了近似值，总体上反映了各被试间的曝光率的平均值，也即在一定程度上并不能完全反映出两两被试之间的重叠率；（4）在实验中，MFI在统一量纲分数较低，其中一个主要原因是其值过大；此外统一量纲并没有考虑Bias，是因为Bias微乎其微的变化也会对统一量纲产生较大影响，所以如何找寻一种能够即不受较大相对差的影响，也不受较小相对差的影响的综合评价方法也有待做进一步的研究。

[1]陈平，丁树良，林海菁，周婕.等级反应模型下计算机化自适应测验选题策略[J].心理学报，2006，38（3）：461-467.

[2]程小杨，丁树良，严深海，朱隆尹.引入曝光因子的计算机化自适应测验的选题策略[J].心理学报，2011，43（2）：203-212.

[3]戴海琦，陈德枝，丁树良，邓太萍.多级评分题计算机自适应测验选题策略比较[J].心理学报，2006，38（5）：778-783.

[4]鹿士义，张坚.题目曝光控制的动态a分层法[J].中国考试，2011（9）：3-9.

[5]漆书青，戴海崎，丁树良.现代教育与心理测量学原理[M].北京：高等教育出版社.2002.

[6]詹沛达，王立君.CAT分层选题策略新探——最大信息量组块分层策略[J].中国考试，2012（6）：10-14.

[7]Barrada，J.R.，Mazuela，P.，&Olea，J.Maximum information stratification method for controlling item exposure in computerized adaptivetesting.Psicothema，2006（18）：156-159.

[8]Chang，H.H.，&Ying，Z.a-stratified multistage computerized adaptive testing.Applied Psychological Measurement，1999，23（3）：211.

[9]Chang，H.H.，Qian，J.，&Ying，Z.a-Stratified multistage computerized adaptive testing with b blocking.Applied Psychological Measurement，2001，25（4）：333.

[10]Hambleton，R.K.，&Swaminathan，H.Item response theory：Principlesand applications.Hing-ham，MA：Kluwer.1985.

[11]Lord，F.M.A Broad-range tailored test of verbal ability.Applied Psychological Measurement，1977（1）：95-100.

[12]Revuelta，J.，&Ponsoda，V.A comparison of item exposure control methods in computerized adaptive testing.Journal of Educational Measurement，1998（35）：311-327.

[13]Segall，D.O.A sharing item response theory model for computerized adaptive testing.Journal of Educational and Behavioral Statistics，2004（29）：439-460.

[14]Sympson，J.B.，&Hetter，R.D.Controlling item-exposure rates in computerized adaptive testing.In Proceedings of the 27thannual meetingof the Military Testing Association（pp.973–977）.San Diego，CA：Navy Personnel Researchand Development Center.1985.

[15]Weiss，D.J.Improving measurement quality and efficiency with adaptive testing.Applied Psychological Measurement，1982，6（4）：473.

[16]Weiss，D.J.，&Kingsbury，G.Application of computerized adaptive testing to educational problems.Journal of Educational Measurement，1984，21（4）：361-375.