面向实际工程应用的线性代数教学研究
王炯琦,冯良贵,周海银
(国防科学技术大学理学院,湖南长沙410073)
线性代数(Linear Algebra)是讨论矩阵理论、与矩阵结合的有限维向量空间及其线性变换理论的一门学科[1],是高等院校理工、经济类专业重要的数学基础课,具有广泛的应用性,对提高教师和学生的数学素养、训练与提高学生的抽象思维能力与逻辑推理能力都具有重要作用[2]。然而,该课程本身具有概念抽象、结构复杂、计算强度大等特点,不仅消磨了学生的学习积极性,也使得教师和学生难以将所教或所学的理论方法应用到解决实际问题中,从而失去了线性代数应有的基础应用性作用。
为培养学生学习线性代数的学习兴趣,使线性代数真正与实际应用和实际问题相结合,发挥其基础应用性课程的作用,近年来,众多从事线性代数的教学、教育的工作者,积极探索实际问题驱动的线性代数课程教学理念,研究该课程的直观性教学思想和方法,并形成基于问题解决的线性代数课程的教学设计模式,包括问题背景下的教学内容组织、课程教学设计及现代化教学运用等[3-5],取得了一定的效果。
近5年来,紧密结合国防现代化建设的需求,我校线性代数教学团队,以物理背景为依托,以线性代数方法创新为突破,以国防建设工程、型号应用为目的,实践了一条以理论教学促进工程发展、科研实践丰富理论教学应用的教学、科研相互促进的良性发展模式。一方面,鼓励从事线性代数教学的教师参加科研活动,加强其科研背景,引导其形成自己的科研方向;通过参加科研工作,使得教师的知识结构更加全面合理,知识不断更新,教师的思路和视野不断开阔。另一方面,科研研究的成果、积累的素材积极的融入到线性代数课程教学中,丰富了教学实验案例,更新了教学理念、教学方式与手段,培养了学生较强的线性代数实际应用能力,适应了新时期人才培养的目标。
下面,以实际例子来说明线性代数教学中矩阵迹的实际工程应用。
一 问题的提出
设有N个传感器对状态向量X∈Rn×1进行线性测量,如图1,观测方程为:
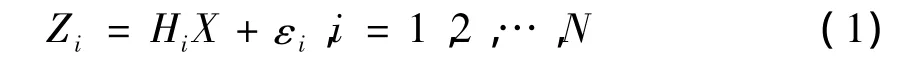
其中 Zi∈ Rmi×1为观测向量,Hi∈ Rmi×n为列满秩观测矩阵,观测误差εi∈Rmi×1满足如下假设:
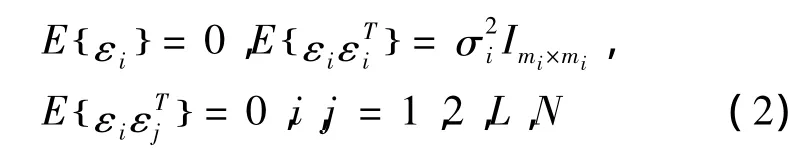
现考虑如何通过观测数据融合,获得关于目标状态向量的最优估计,并分析估计的性质。
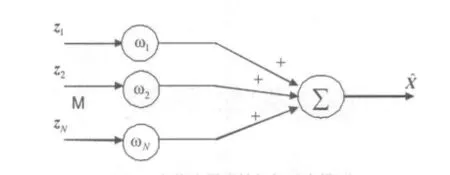
图1 多传感器线性加权融合模型
二 线性融合模型及融合估计精度
对于式(1)的观测模型,式(2)的实际工程意义是:传感器观测误差为零均值,不同传感器的观测是不相关的,同一传感器的各测量通道的测量是不相关且等精度的,如果各通道精度不等,则易通过归一化处理为等精度[6]。
(一)线性融合估计
下面的定理给出了式(1)中状态向量的估计。定理1 模型(1)下状态向量X的最优估计为
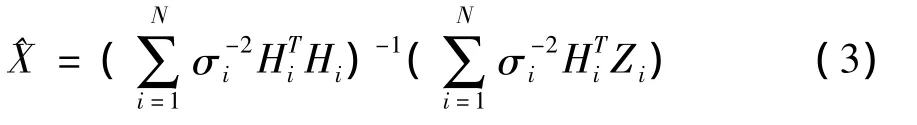
估计的均方误差MSE为
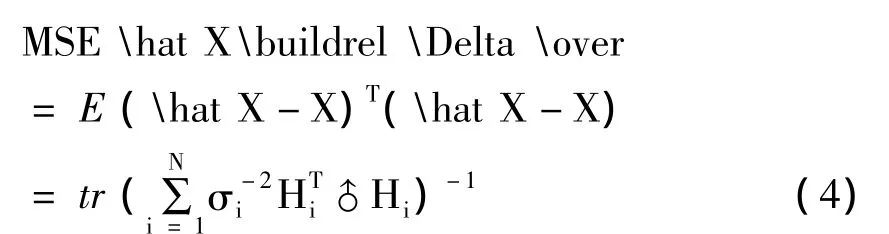
其中tr为方阵的迹。

其中Eε=0,EεεT=I。
由最小二乘估计准则[7],知X的最优估计为:
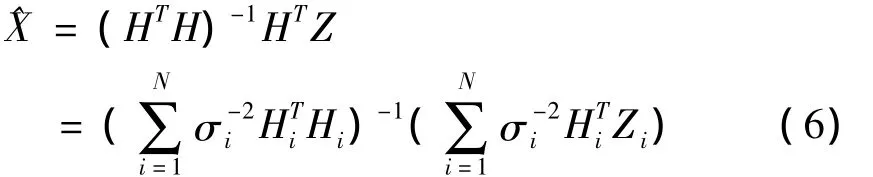
从而
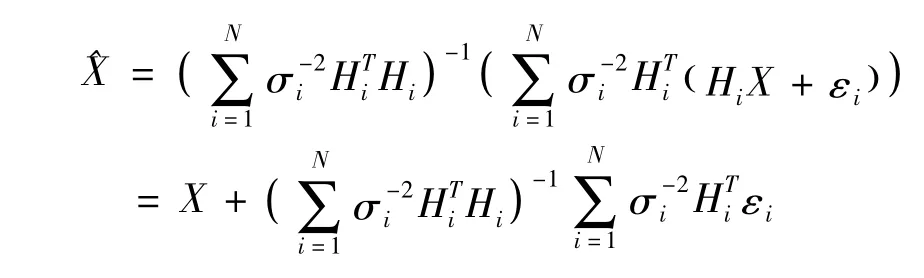
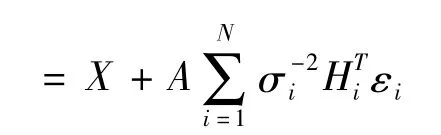
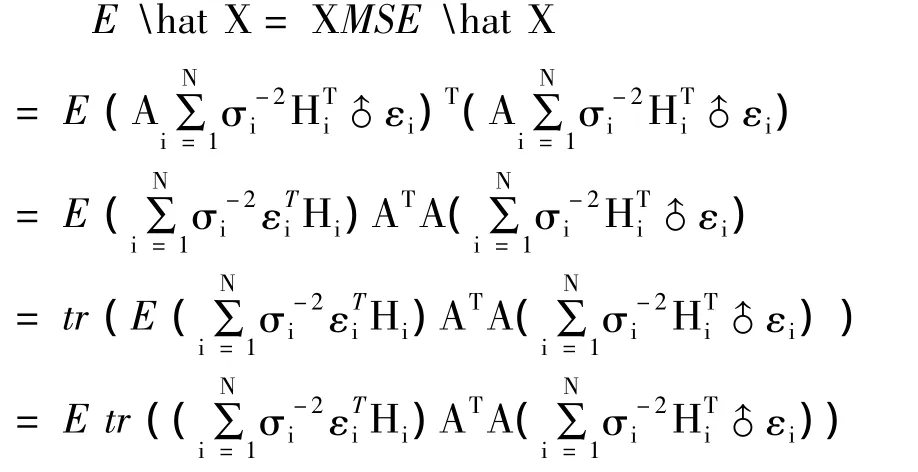
利用矩阵迹的可交换性[8]及E tr A=tr E A,因此
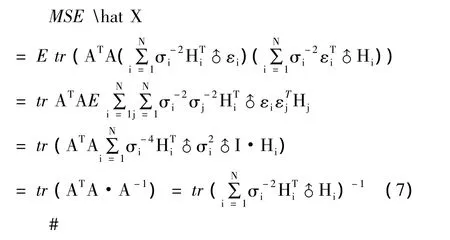
(二)融合估计性质及精度分析
从定理1可知,对于多传感器线性观测模型,状态向量的最优估计^X实际上为各传感器观测数据Zi的加权和,其融合加权权值为
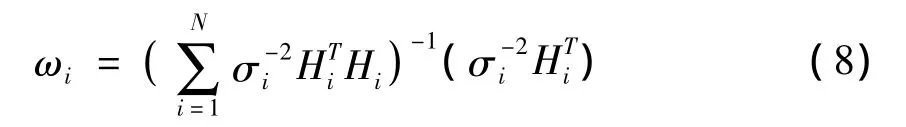
其实际工程意义为:当状态向量为一维的,各传感器直接对状态进行观测时,状态量的最优估计为各传感器观测值的加权平均,其权为:
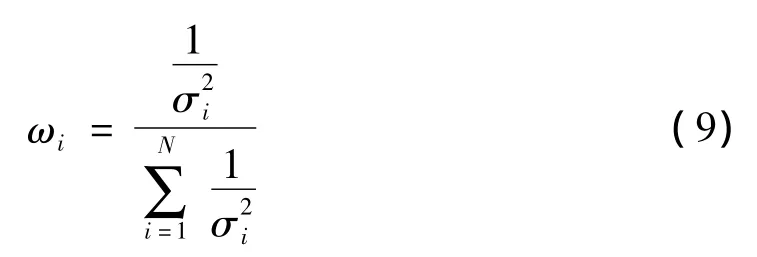
式(9)的分母是权值的归一化,即各传感器权值的和为1,分子为第i个传感器的观测精度;此外,假设N个传感器的观测信息精度相等,即σ1=σ2=,Λ,=σN=σ0,则N个传感器融合后的均方误差MSE[hat X]=♂/N,表明N个相同精度传感器的输出信息融合后精度提高到单个传感器的倍;假如传感器的测量精度有高低之分,最低精度与最高精度分别为和,则融合精度为
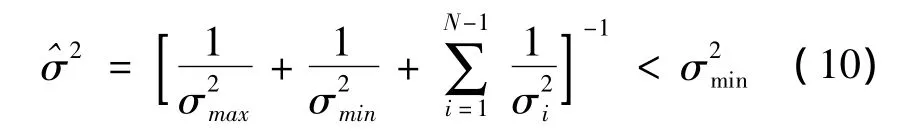
这说明通过多传感器测量,采用最优加权信息融合方法,能够提高一维系统状态估计的精度。
下面考虑模型(1)下的多传感器线性融合估计性质。显然,式(1)中,仅用第i个传感器进行线性观测,其最优估计为
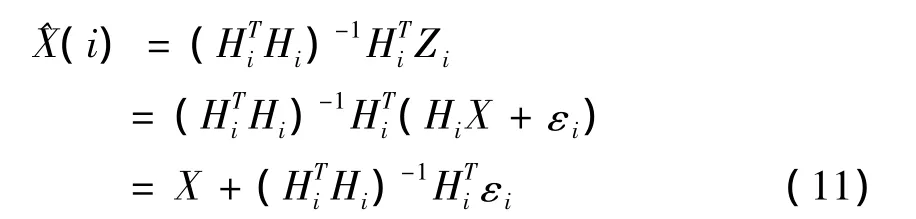
且
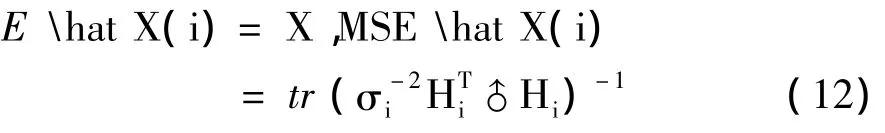
而由定理1知,N个传感器线性观测下得到的最优估计的均方误差为
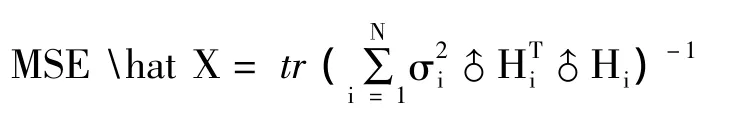
定理2 多传感器线性最优融合的精度优于任意单一传感器测量给出的最优估计精度,即
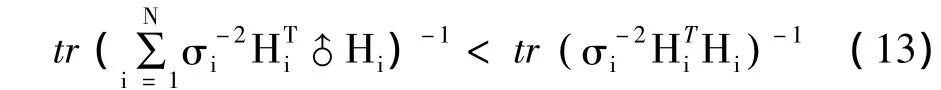
三 定理2的证明
由于 Hi∈ Rmi×n为列满秩矩阵,σ2i>0,从而为正定矩阵,记为 Bi,i=1,2,…,N 。定理2可转化为如下命题。
命题:已知 Bi> 0,i=1,2,…,N ,求证 tr(B1+B2+…BN)-1<tr(Bi)-1。
方法1:直接证明法
证:因为
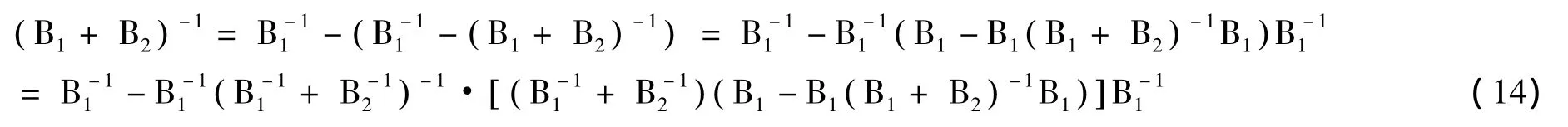
而
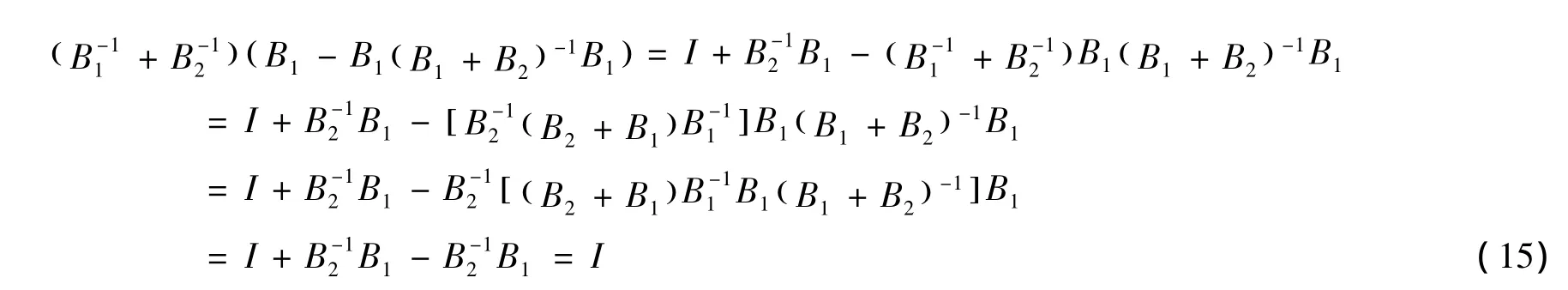
从而
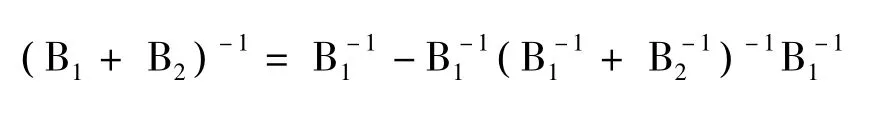
故
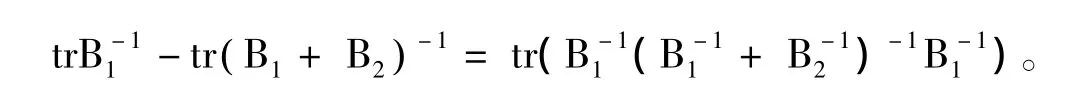
由于正定矩阵的逆、正定矩阵的和以及正定矩阵的合同变换都是正定的[8],所以是正定矩阵,其特征值均大于0,即
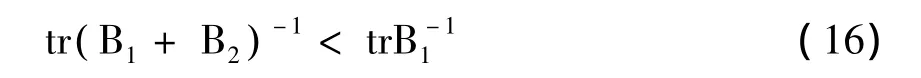
上式推广,即得
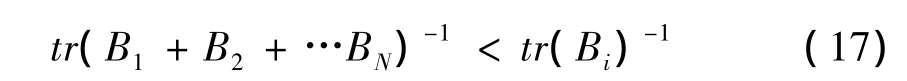
#
方法2:利用矩阵相似、矩阵合同性质
证:因为B1正定,则B-11也正定,从而存在矩阵 P1,使得 PT1B-11P1= I。另一方面,易知PT1B-12P1也为正定矩阵,从而存在正交矩阵P2,使得PT2PT1B-12P1P2=Λ,其中Λ为对角矩阵,且对角元素 λ1,λ2,…,λn> 0 。令 P=P1P2,Q=P-1,即
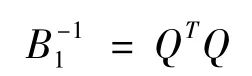
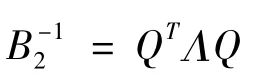
(B1+B2)-1=QT(I+Λ)-1Q
令 QT= [q1,q2,…,qn],qi∈ Rn×1,i=1,2,….n ,从而
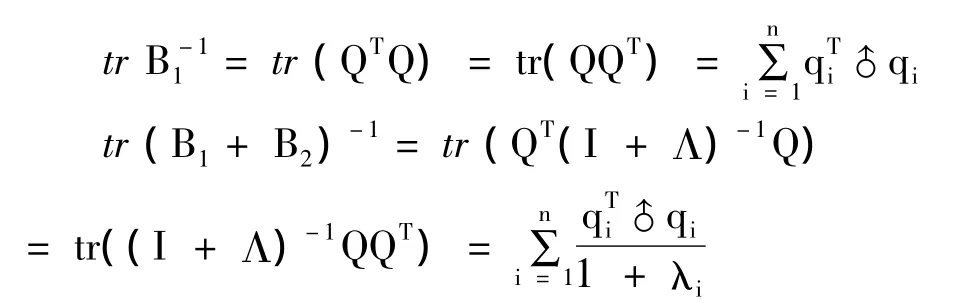
从而
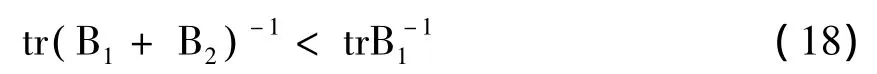
上式推广,即得
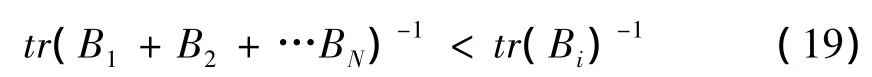
#
定理1和定理2的实际工程意义在于:
注释1:多传感器线性观测系统的最优状态估计精度由单一传感器的测量精度σ2i和观测矩阵Hi等系统参数共同决定。
注释2:在由多个传感器组成的线性融合系统中,观测矩阵和测量精度分别为 Hi和 σ2i,则相同的多传感器融合系统,状态估计的精度也相同。
注释3:多传感器线性融合系统的最优状态估计精度比基于单一传感器的测量信息的状态估计精度要高。
注释4:利用的测量信息越多,则最优估计的精度就越高,即多传感器信息融合在一定程度上能提高融合系统的状态估计精度。
以上结论对于实际工程中高性能多传感器融合系统的设计提供了重要的理论基础。
四 结论
线性代数是一门应用性、实践性极强的数学基础课程。实际工程中的许多物理现象均能够提炼出相应的数学理论和方法,而所提炼的数学理论反过来又能解释或指导工程应用。然而目前大多数线性代数的课程教学严重脱离实际应用,使得学生无法理解或难以将所学的理论方法应用到解决实际问题中,降低了学习的兴趣和学习的效率。
多年来,我校线性代数教学团队一直秉承“以实际问题驱动的线性代数教学”理念和方法,以物理背景为依托,以线性代数方法创新为突破,以国防建设工程、型号应用为目的,实践了一条以理论教学促进工程发展、科研实践丰富理论教学应用的教学、科研相互促进的良性发展模式。本文以线性代数教学中矩阵“迹”的实际工程为例,阐述了我校线性代数教学团队积极将科研研究的成果、积累的素材有效地融入到线性代数课程教学中,丰富了教学实验案例,很大程度上提高了学生学习线性代数的兴趣,使得学生们“在研究中学习、在学习中研究”,培养学生的研究能力和创新能力。
[1]李尚志.线性代数[M].北京:高等教育出版社,2006.
[2]李亚红,魏建洲.关于线性代数直观性教学的一些思考[J].数学教育研究,2012,31(1):49-52.
[3]陈建华,李立斌,凌智,等.基于问题解决的线性代数课程教学设计研究[J].高等理科教育,2011(4):117-120.
[4]LAY D.C.线性代数及其应用[M].北京:电子工业出版社,2004.
[5]王瑞,夏爱生,刘艳娜,等.线性代数(非数学专业)整体教学的实践与认识[J].大学数学,2011,27(6):11-14.
[6]王炯琦.信息融合估计理论及其在卫星状态估计中的应用[D].长沙:国防科技大学理学院,2007.
[7]茆诗松,王静龙,濮晓龙.高等数理统计:第2版[M].北京:高等教育出版社,2006.
[8]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

