土木类专业高等数学教学工程化的研究与实践
王 芳
(长沙理工大学数学与计算科学学院,湖南长沙410076)
在20世纪的最后20年中,高等教育的数学教学改革已引起各国高等数学教育界的高度重视。然而,由于数学科学既有悠久的教育历史,又有惯用的教学方法,既有成熟的过去,又有辉煌的现代,各国数学家与数学教育家对改革都持慎之又慎的态度,改革步伐稳健而又缓慢。
我国高等数学课程的教学体系和教学内容,沿袭于1930—40年代前苏联研究的数学课程。数十年间虽有几次改革,但其基本内容和体系没有实质性的变化。随着社会飞速发展和科学技术日新月异的进步,高等数学的内容和体系已经不能适应社会发展的需要[1]。在科学技术飞速发展的21世纪,实力的竞争就是人才的竞争,社会的巨变、经济的发展、职业流动的加快、科学发展的综合化和复杂化都对人才素质提出了新的要求,对高级创新人才的需求也不断增加。为了迎接新世纪的挑战,目前国内已经有很多高校的教师正在着手于高等数学课程教学与理工科专业相结合的模式的探索与研究[2-4]。高等数学作为土木类专业学生的一门重要的公共基础课,课程学习的效果对后续专业课程的学习和学生的长期发展有着深远影响,并必然影响到合格工程人才的培养。
2006年,教育部数学与统计学教学指导委员会对工科类本科数学基础课程颁布了一个教学基本要求,要求指出:教师在传授数学知识的同时,要努力培养学生进行抽象思维和逻辑推理的理性思维能力、综合运用所学的知识分析问题和解决问题的能力以及较强的自主学习能力,逐步培养学生的创新精神和创新能力。根据该要求,原属于必须掌握的抽象的经典定理证明,现已变成了解性内容,同时新增一些应用性强的内容,更强调数学结论的应用。这一要求进一步明确了将高等数学的知识应用到各行各业的重要性,而对土木类专业的学生而言,数学既是专业课的基础,又是专业课的工具,它为后续专业课的学习提供了必备的数量分析方法和计算手段。而传统的高等数学的教学模式,为了不影响数学知识的严密性,大多数教师都是为了传授纯粹的数学知识而展开教学工作,这无法让学生深刻理解高等数学与其所学土木类专业之间的紧密联系,更无法挖掘出高等数学所学知识在其土木类专业中的应用,因而没有很好地激发学生学习兴趣,取得令人满意的教学效果。
一 高等数学课程教学工程化的目的与意义
土木类专业高等数学课程教学工程化是指在教学过程中,教师应该树立工程化的教学理念,结合土木类专业的工程背景知识,将数学中的应用问题转化成土木类专业中的工程实例进行教学。运用工程化的思维进行教学和研究,即一方面将土木类专业工程中的数学问题作为高等数学系列课程教学的重要教学内容,另一方面在数学问题的讲解中引入工程的逻辑理念,像对待工程问题一样展开高等数学课程的教学。这样不仅能使学生深刻地理解高等数学这门课程与土木类专业的紧密联系,熟知高等数学教学中的理论知识的应用价值,更能使学生形象生动地理解部分枯燥难懂的数学问题,使得高等数学课程教学效果大幅提升。
(一)更新土木类专业高等数学课程教学理念
打破传统的高等数学课程的教学模式,将工程化的理念引入到教学过程中。针对土木类专业形成全新的、立体化、工程化的教学资源,有效地吸取土木类专业的工程背景知识,促进数学知识在土木类专业的应用。
(二)丰富高等数学课程教学手段,提高教学效果
在工程化的视角下,鼓励教师积极使用现代教育技术理论,以网络课程建设平台、课件制作、视频资源开发等为支撑,实现信息技术与高等数学系列课程的整合,利用计算机多媒体技术与计算机辅助数学的软件,将复杂抽象的数学知识的形成过程形象化、图形化、动态化。只有提高土木类专业高等数学课程的教学效果,有效地促使土木类专业学生理解高等数学课程的实际应用价值,才能提高学生运用数学知识的能力,激发学生学习高等数学的积极性,为培养合格的土木类专业工程人才奠定坚实基础。
二 实施高等数学课程教学工程化的具体举措
(一)改革教学理念
通过宣传引导,促进授课教师树立工程化的教学理念。根据理工科院校土木类专业学生的专业设置情况,组织高等数学任课教师与土木类专业任课教师进行讨论,对土木类专业所需数学知识做细致全面的考虑。将高等数学系列课程的任课教师实施分组式、包块式教学,针对土木类专业设置稳定的教师队伍,在今后的教学中,该教学团队认真钻研土木类专业的专业背景知识和专业教材,与讲授专业课的任课教师定期举办教学改革的研讨活动,相互学习,相互探讨,梳理和归纳出相关的数学知识,进行集体备课,探究应用到该专业的数学知识的根源地和目的地,实现师资队伍的工程化。
(二)改革教学资源
针对土木类专业的学生配备相应的教学资源。其教学资源除了优化重组高等数学系列课程教材中的经典数学内容外,负责土木类专业的教学团队在备课时应该充分考虑所授课学生专业中所涉及的数学知识,对教学内容进行适当的调整,针对土木类专业的专业基础课中所需要的数学知识的先后顺序对教学内容进行排序,真正做到高等数学系列课程的数学知识为后续专业课程服务。在对相关的数学知识进行应用举例时,以工程实例为背景,将数学知识与专业知识紧密联系起来,将学生所学专业中碰到的数学问题、数学概念、数学计算在高等数学的教学过程中充分体现,将土木类专业中的实际问题或者工程技术问题转化成数学中的应用问题进行讲解。积极主动地与土木类专业的专业任课教师沟通与交流,定期展开教学改革的研讨活动,根据土木类专业知识的不断更新而对其相应的教学资源作出适当调整,做到理工科大学土木类专业的高等数学教育既吸收数学学术的最新成果,又跟踪工程技术的发展。另外,在讲解高等数学中的具体概念时,要充分考虑到土木类专业的特点,在引入新的数学定义时,不妨以专业中将会出现的实例作为引例。例如,微积分在土木类专业中占据很重要的地位,主要表现在:
①土木类专业学科中的有些概念由微积分的相应概念给出,如内力在一点处的分布集度——应力就是轴向拉力F对截面A的导数,即:
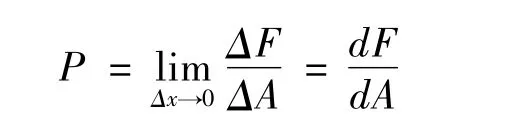
通过导数给出了应力的概念后,为以后的应力分析奠定了基础。
②很多原理、定理或概念间关系通过微积分表达,如变形体虚功原理、功和互等定理、荷载集度剪力图和弯矩图之间的关系等。
③专业计算运用微积分,如剪应力计算公式、梁的变形计算、结构位移计算、梁及钢架的平移等等[5]。
因此,我们在制定土木类专业高等数学微积分这一部分的教学资源时,一定要全面研究其专业知识中所需要的数学知识,在引入微积分的数学概念时,为了强调数学知识在专业中的应用,可将后续专业课程将出现的实例作为引例引入其相应的数学定义,以加强数学知识与专业知识的深度融合。例如,我们常常利用变速直线运动的瞬时速度,曲线的切线的斜率引入导数的定义,针对土木类专业的学生我们不妨给出第3个引例即内力在一点处的分布集度等相关实例来进一步阐述导数的定义,在对导数的概念进行应用举例时,我们可以强调一些和土木类专业密切相关的实例,如梁横截面上的弯矩、剪力与梁上作用的外荷载间的关系、混凝土抗压强度增长速度的计算等,并强调剪力函数就是弯矩函数的导函数等等。
(三)改革教学手段
鼓励教师积极引入现代教育技术手段,实现信息技术与高等数学系列课程的整合,利用计算机多媒体技术与计算机辅助数学的软件,将复杂抽象的数学知识的形成过程形象化、图形化、动态化,充分利用学校现有的网络课程教学平台,及时上传教学材料,补充教学内容,将高等数学系列课程中的数学知识延伸至土木类专业知识中,将学生所学专业中出现的工程数学问题上传到网络课程教学平台上,以供学生课后思考。同时也应该在高等数学系列课程的教学学时中安排少量的实验教学课时,为学生营造一种新型的教学环境,使学生学习高等数学的过程变成“自己动手实验—观察发现—猜想验证—合情推理—动脑设计”的过程,真正实现高等数学教学过程的工程化。
总之,理工科院校土木类专业高等数学的课程教学要从培养学生的数学能力出发,以为专业课、专业基础课服务为目的,认真研究两者之间的关系,梳理出两者之间的必然联系,针对土木类专业的高等数学建立全新的、立体化的、工程化的教学资源。这需要高等数学任课教师付出很多的心血,也需得到相关的职能部门与负责这两门课程的学院之间的密切配合。只有这样,才能完全实现土木类专业高等数学课程教学的工程化。
[1]黄力民.50年大学工科数学教育之检讨[J].高等工程教育研究,2002(1):47-51.
[2]罗建书,倪谷炎.工科数学分析教学改革初探[J].高等教育研究学报,2006(2):43-45.
[3]饶三平,冯喜全.高等数学教学与专业结合模式的初步探索[J].科技信息,2008(33):21-22.
[4]陈东,张立新,贾文敬.数学素质与应用型人才[J].大学数学,2006(4):11-13.
[5]孙福兴.建筑工程基础数学[M].北京:中国建筑工业出版社,1980:1-308.

