项目实施进度控制的理想状况

王小委 王 旭 朱炉军

(重庆交通大学，重庆 400074)

0 引言

施工项目进度比较分析与计划调整是施工项目进度控制的主要环节。其中施工项目进度比较是调整的基础。常用的一种比较方法是“香蕉曲线”法[1-3]。“香蕉曲线”是由两条S形曲线组合而成的闭合曲线，其一是计划以各项工作的最早开始时间安排进度而绘制的S形曲线，称为ES曲线;其二是计划以各项工作的最迟开始时间安排进度而绘制的S形曲线，称为LS曲线。如果以ES曲线来安排项目的实施进度，导致的结果将是在项目的实施初期投入过量的人力、物力和财力，这显然是我们所不希望的;但如果以LS曲线来安排项目的实施进度，又会出现后期赶工的现象，不利于项目健康的实施。因此，一般认为在项目实施中进度控制的理想状况是任一时刻按实际进度描绘的点应落在“香蕉曲线”区域内，如图1所示。

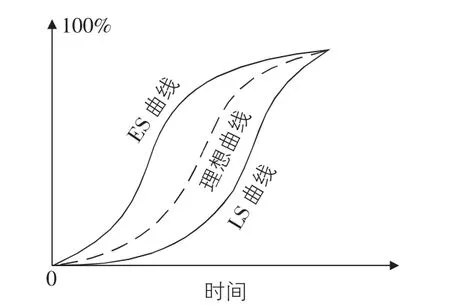
图1 香蕉曲线

按上述想法，下面进行进度控制的理想曲线求解。

1 理想曲线的散点图

采用积分求面积的方法，并引进黄金分割比，可以得出理想曲线满足的积分式。假设ES曲线函数形式为S1=S1(t)，LS曲线函数形式为S2=S2(t)，理想曲线函数形式为f=f(t)，则有:

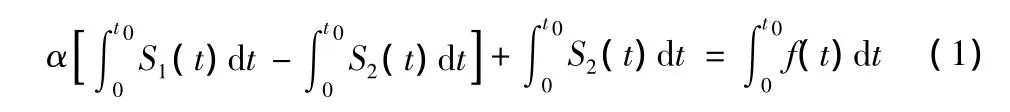
其中，α为黄金分割比，取0.618。

上面的处理方法是比较常见的，有其科学性和合理性。问题是如何求解该积分式。显然，ES曲线方程和LS曲线方程可以根据项目实施的进度计划得出，则该积分方程中唯一不确定的就是理想曲线方程，但直接求出该曲线方程仍是办不到的。下面采用高斯积分公式处理该问题[4-6]。

根据高斯积分公式有:

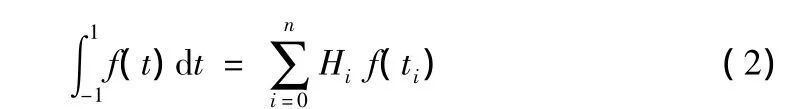
则方程(1)中各积分式可变为如下形式:

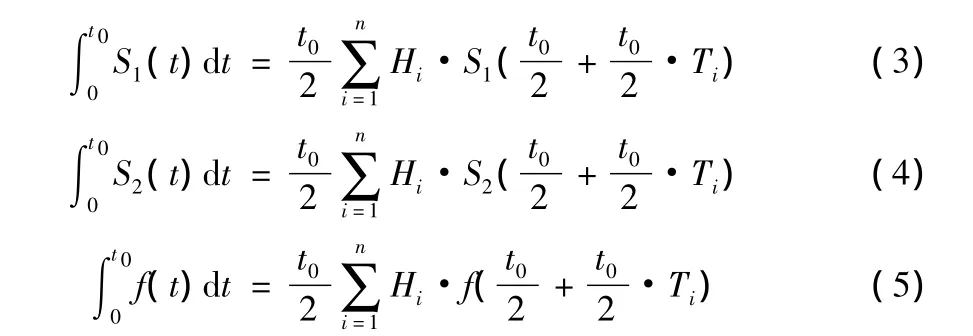
将式(3)～式(5)代入式(1)中整理得:

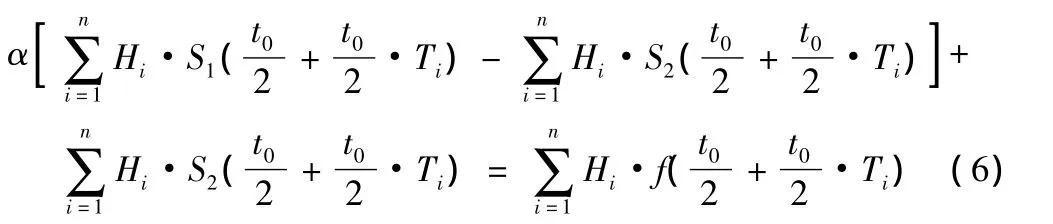
若取节点数为1，即n=1，Hi=2，Ti=0，则式(6)可简化为:

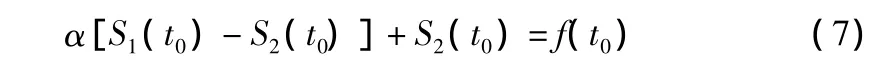
故按上述方法，可以求出理想曲线的散点图。

2 散点的拟合

对于散点拟合问题，常采用的方法是最小二乘法，该方法有其优点，但也有缺点，如当离散数据量比较大、形状复杂，就需要进行分段(分块)拟合和平滑化，这在实际中往往带来困难。

采用移动最小二乘(MLS)法建立一种新的曲线拟合方法，这种方法能够克服以上困难，并且具有许多其他优点。Lancaster和Salkauskas最先在曲面生成中使用了MLS法，后来Belystachko将其应用于无网格方法中[9，12]。该方法的具体操作过程如下:

1)建立拟合函数。

在拟合区域的一个局部子域上，拟合函数f(x)表示为[10，11]:

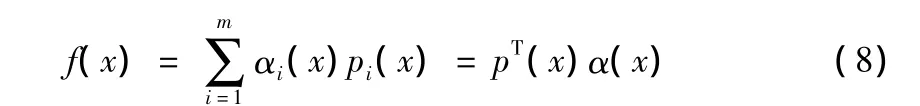
其中，α(x)=[α1(x)，α2(x)，…，αm(x)]为待求系数，它是坐标 x的函数;P(x)为基函数，P(x)=[P1(x)，P2(x)，…，Pm(x)]，它是一个k阶完备多项式;m为基函数的项数。

出院指导：①避免长时间坐卧，尤其是交叉腿坐位，应定时活动肢体，患者下肢自我按摩或嘱咐家属多进行下肢肌肉的按摩，以促进血液循环；②注意清淡饮食，避免寒冷刺激，戒烟；③下肢静脉曲张或存在深静脉血栓危险因素的患者建议穿弹力袜。

考虑下面的加权离散范式:

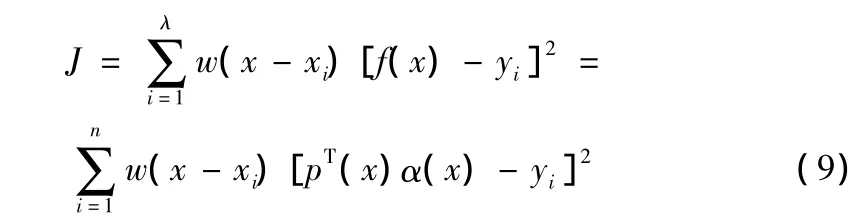
其中，n为影响区域内节点的数目;f(x)为拟合函数;yi为x=xi处的节点值;w(x-xi)为节点的权函数。

为确定系数α(x)，式(9)应取极小值，式(9)两端对α求导有:

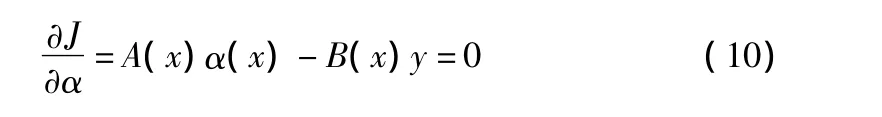
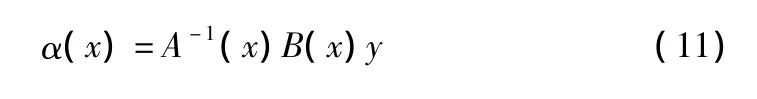
其中，

将式(11)代入式(8)，可得MLS拟合函数:

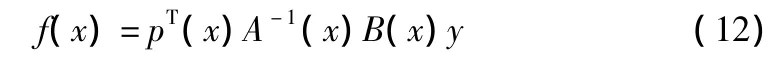
2)权函数的选取。

常用的权函数是样条函数[7，8]，记 S=x-xi，s'=S/Smax，三次样条权函数如下式:

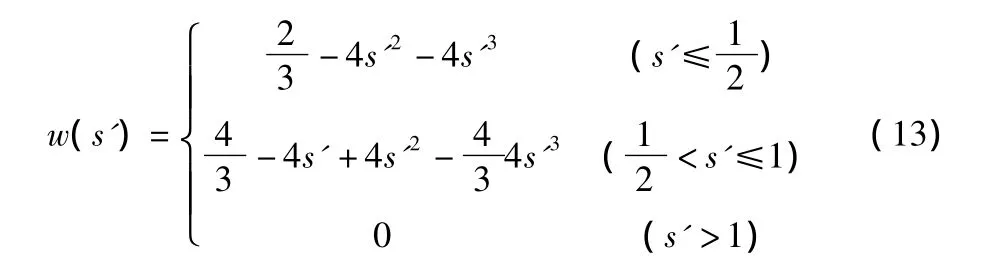
其中，Smax为权函数的支持域(即x的影响区域)，示意图见图2。

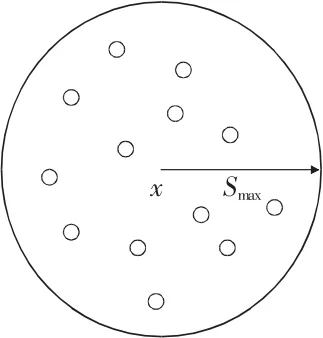
图2 影响区域

故利用上述移动最小二乘法可以将散点图进行拟合。

3 算例分析

现将上述方法运用于某实际工程实施进度控制中。该工程总工期30 d，进度控制的ES曲线和LS曲线的时间与完成百分量的关系见表1，表2。

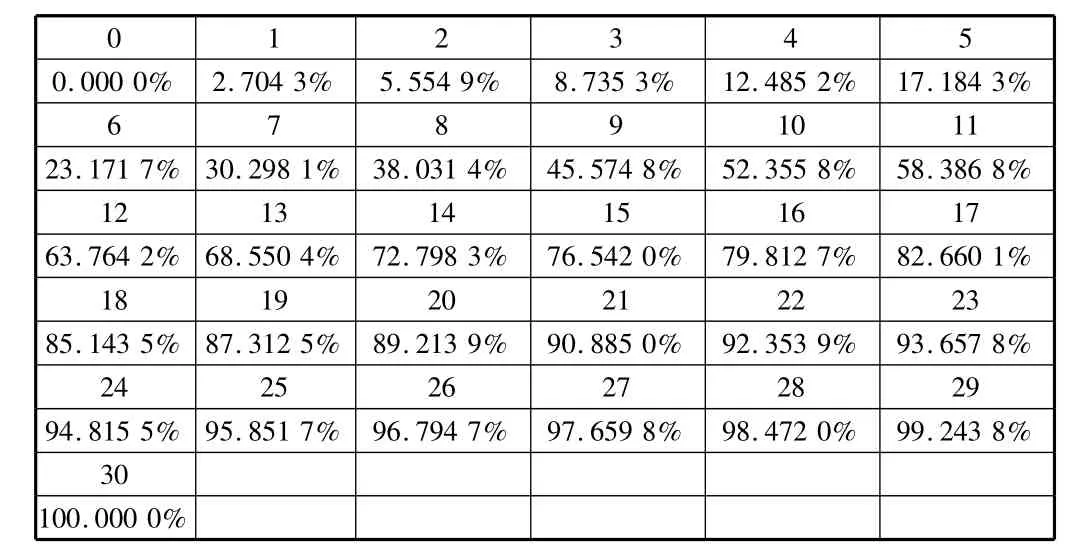
表1 ES曲线进度表

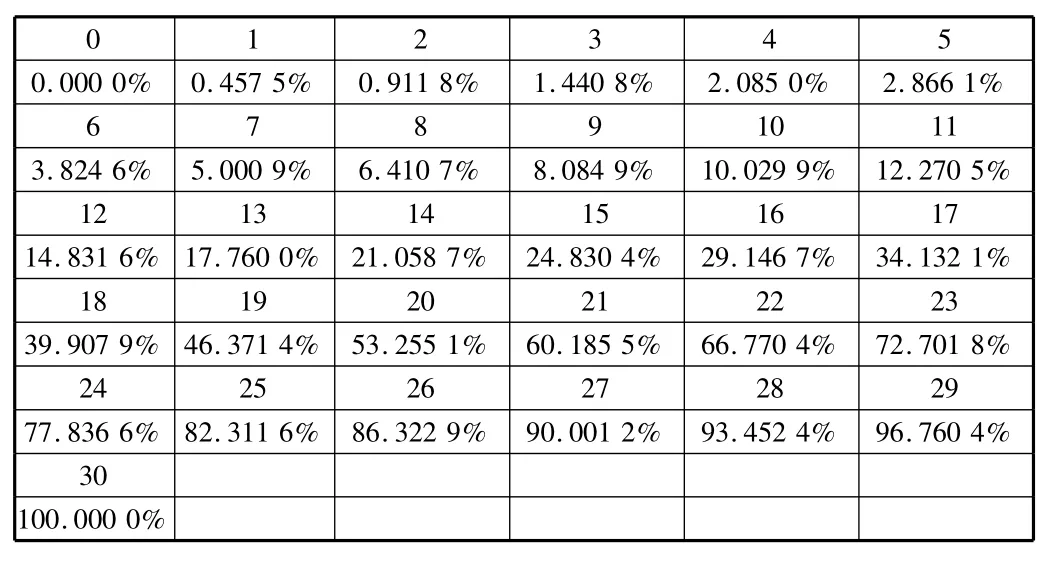
表2 LS曲线进度表

为简单起见采用1节点积分，得出散点，如表3所示。

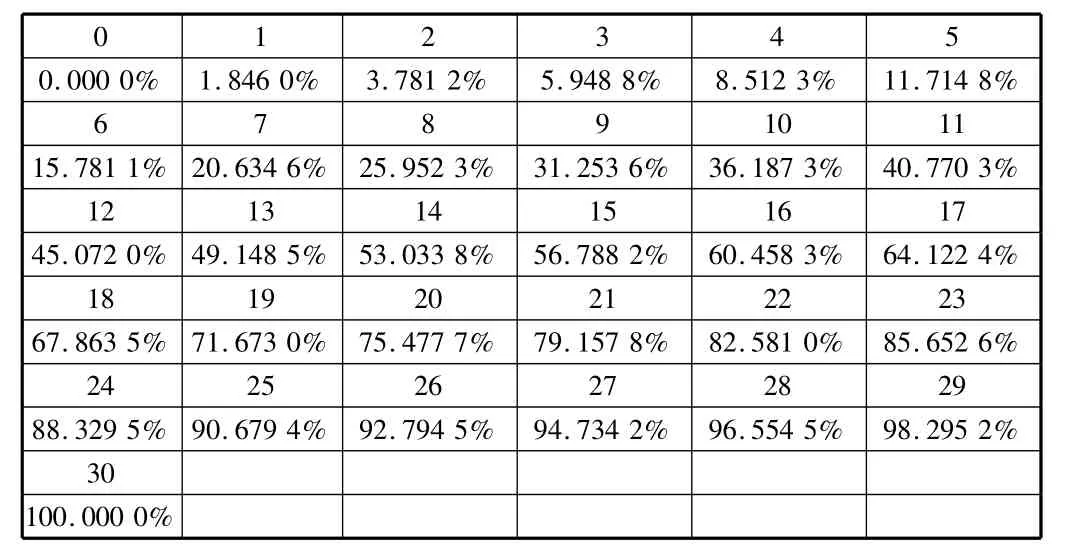
表3 理想曲线进度表

画出ES曲线，LS曲线和理想曲线的散点图，并对上述散点进行拟合，拟合过程采用线性基函数p(x)=[1，x]T，结果见图3。

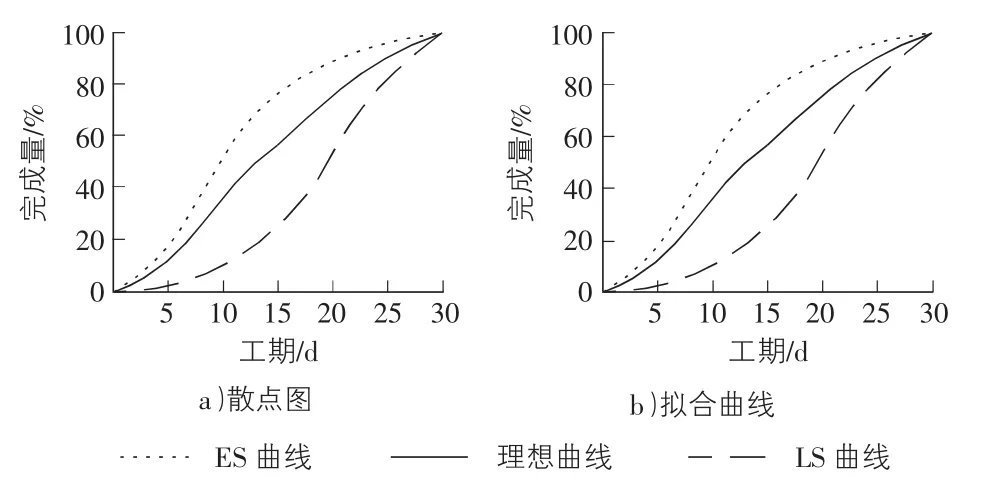
图3 项目实施进度控制曲线

4 结语

以高斯积分和移动最小二乘法理论为基础，针对项目实施进度控制中存在的问题，提出了一种较为合理的进度控制曲线的确定方法，并将该方法运用于工程实践中，结果可行。但该方法也有自身的缺点，为了获取更高的精度，需得花费大量时间用于计算，手算难度高，当然在计算机飞速发展的时代这已不是问题。

[1] 张智洪，张玉强.水云工程项目管理[M].北京:人民交通出版社，2011.

[2] 丁士昭.工程项目管理[M].北京:中国建筑工业出版社，2006.

[3] 李庆扬，王能超，易大义.数值分析[M].第5版.北京:清华大学出版社，2008.

[4] 李卫军，操华胜.高斯—勒让德积分公式的加速算法研究[J].地理空间信息，2008，6(4):113-115.

[5] 朱洁菡.高斯—拉盖尔求积公式[J].科技信息，2010(23):687-688.

[6] 许小勇，金建华.Newton-Cotes求积系数与复合Gauss求积算法的程序设计[J].重庆文理学院(自然科学版)，2009，28(4):15-17.

[7] 管 斌，高 扬，王成宾，等.基于递推最小二乘的在线罗差校正方法[J].中国惯性技术学报，2012(1):69-73.

[8] 刘 明.普通最小二乘法的几何分析[J].方法应用，2012(8):90-91.

[9] 倪 慧，李 重，宋红星，等.带插值条件的移动最小二乘曲线拟合[J].浙江理工大学学报，2011，28(1):135-139.

[10] 张 瑜，聂玉峰，李义强.振荡函数的移动最小二乘逼近方法[J].航空计算技术，2011，41(1):30-33.

[11] 任红萍，程玉民，张 武.改进的移动最小二乘插值法研究[J].工程数学学报，2010，27(6):1021-1029.

[12] 李世飞，王 平，沈振康.利用移动最小二乘法进行深度图像曲面拟合[J].吉林大学学报(工学版)，2010，40(1):229- 233.