无碴轨列车引起的竖向振动在土体中的传播研究

廖袖锋，黄宾，葛勇

（1重庆市合川区建设工程质量监督站，重庆 401520；2宜宾市建设工程质量安全监督站，四川宜宾 644000；3四川省雅安市城乡规划建设和住房保障局，四川雅安 625000）

0 引言

城市轨道交通和高速铁路的发展，加剧了轨道交通对环境振动的影响。近年来，普通公众、政府以及学者[1]都逐渐开始关注轨道交通引起的环境振动问题。随着人们对生活环境的要求越来越高，加强对轨道交通的环境振动的控制就成为必然。

列车运行引起的环境振动，其实质是土体受到列车振动激励后，周边土体质点先后发生振动，由轨道向附近传递振动的过程。振动在土层介质中的传播，是能量的传播过程。高速列车等轨道交通运行时产生的振动是以应力波传播[2]的形式传播的，其振动特性及振动强度与土的刚度及几何特性等因素有关。通常将应力波分为弹性波和塑性波，弹性波是指其应变没有超过土体的弹性极限，而塑性波则是其应变超过了土体的弹性极限，塑性波在传播的过程中波形会发生变化。申跃奎[3]等认为当土的应变ε<10-4时，土体处于理想弹性状态，土体骨架发生变形后能自动恢复。在土地的动力响应分析过程中可以采用等效线性模型。尽管在列车运行过程中，塑性变形可能会出现在靠近轨道区域的土体中，但由于土体的振动幅值相对较小，所以将土体作为弹性介质考虑，认为其处于弹性阶段。Kurzweil[4]研究了不同土层在列车运行引起振动时振动波的衰减特性、传播路径等。青木一郎[5]研究了列车运行引起的结构振动发生的机理。Hayakawa[6]对振动波在地面和地表以下的传播规律进行了研究。有限元-边界元耦合法[7]、位移边界元法[8]、有限元-边界元分析法[9]都常常用于研究列车运行引起的振动。在国内夏禾[13]等分别建立了建筑物-土层-路基和轨道-列车的动力模型，对比分析计算了振动在土体中的传播规律及振动响应特性。和振兴[12]运用数值方法和解析方法研究了列车在板式无碴轨上运行时产生的振动在土体中的传播规律。谢伟平[14]基于有限元法分析了列车移动荷载作用下的土体的振动响应，并结合分层法对比分析地基中的振动传播规律。李晓霖[16]和陶连金[15]对隧道衬砌层状地基进行研究，在动力响应分析过程中以列车振动加速度时程作为激励输入，并对振动在地面的传播规律进行了研究。申跃奎[3]利用实测和有限元数值模拟研究了地铁振动在土壤中的传播，并对有限元模型、单元尺寸、阻尼、时间步长及边界等因素进行了讨论。崔正翔[18]的研究表明，阻尼较大时可以有效地减弱振动，而轨道附近为基岩层，其阻尼较小，列车的振动波衰减慢，故周围场地有较高的加速度振级。

1 振动传播的数值分析方法

数值分析和理论解析都是研究振动在土体中传播规律的重要手段，但是对非均匀结构、复杂结构、结构与土体的相互作用、介质非线性特性等问题，数值分析的优越性更为明显。在数值分析中，频域和时域分析都是常用的手段。但是列车振动荷载在频域上频谱较宽，并且土体也是分层的非均匀介质，因此土体的振动用频域的方法计算十分困难。因而，在列车运行引起场地振动的动力响应分析中一般都用时域分析方法。有限元法是将连续的求解域离散，用在每个单元内假设的近似函数来分片的表示求解域上待求的未知场函数，从而使一个连续的无限自由度问题变成离散的有限自由度问题。动力问题的有限元方程为[19]：

式中，[M]、[C]、[K]分别为结构的质量、阻尼和刚度矩阵；和#x(t)$分别为结构的加速度、速度和位移向量；{F为结构的荷载向量。本文采用直接积分法求解列车运行引起的场地振动。其中，Wilson-θ和Newmark-β都是求解非线性方程组最常用、最有效的方法，本文计算采用Newmark-β法求解。

2 列车振动传播的数值模拟

2.1 计算假定

由列车运行引起的土地应变远小于10-4，根据文献[3]的研究，ε<10-4时，土体为弹性阶段。因此，在这类问题中，土体认为处于完全弹性阶段，在数值模拟中假定：

(1)假定土体为弹性模型，弹性体内的各薄层满足均质和各向同性，并且土层之间相互独立。

(2)假定弹性性质不相同的土层之间的界面上均满足位移协调条件，即各层土体之间无相对滑移和分离。

(3)计算方法选取为总应力法。

2.2 有限元法计算模型和单元划分

(1)有限元法计算模型

通常根据计算精度要求、振动能量的大小和计算设备等因素综合确定计算模型的大小。在用有限元法计算列车运行引起的场地振动动力响应时，沈霞[20]认为若不设置人工边界条件，有限元模型的长度应不小于三倍的土层厚度，竖向深度也应大于三分之二的土层厚度。杨永斌[9]则认为土层有限元计算模型的尺寸应为剪切波的波长λs的1～1.5倍。

(2)有限元单元划分

低通效应和频散效应是两种常见的不利现象，在半空间无限土层的动力数值分析中使波的传播性质发生变化。低通效应就是当外界的动力荷载作用在离散的有限单元体上时，那些频率高于离散体系最高固有频率的分量会受到阻止而无法继续传播，高于固有频率的扰动分量才会引起体系内各个质点的振动并且使振动得以传播。

由波动力学的带宽定理可知：?

式中，ω为圆频率，x为空间域，K为波数，t为时间。在进行计算中Δt（Δx）取值越小，能量在时间域（空间域）上就越集中，获得的波数域ΔK（频谱域Δω）就越宽。

研究表明[3]，划分的单元尺寸足够小时可以提高直接运用有限元离散介质模型的解的精度，所以在进行本文类似问题分析时要保证划分的单元足够小。

2.3 计算条件设定

(1)计算时间步长

要想提高有限元计算的稳定性和精度，必须选取合理的计算时间步长Δt。因为如果当Δt取值大时，无法对高频部分进行有效计算，计算结果会不精确甚至导致计算不收敛；如果Δt过小，会消耗大量的时间在迭代计算上，同时也会使累积误差过大。文献[21]认为计算时间步长Δt应为模型自振周期的1/50～1/10最合适。此外激励荷载的频率和采样定理的要求也是时间步长选取的影响因素。综合考虑，本文取时间步长Δt=0.002s。

(2)阻尼矩阵模型

阻尼是表征结构特性的重要参数，本文计算中采用的是Rayleigh阻尼模型[3]：

(3)边界条件

在进行有限元分析前需要根据研究方向选取合理的计算域，然后设置适当的人工边界条件，保证计算符合计算假定。影响人工边界选取的因素很多，比如边界条件的类型、所研究的频率范围、以及激励持续时间的影响。现在比较常用的方法有透射边界（自由边界）、动力映射无限元、叠加边界等。文献[22]中分析对比了多种人工边界后认为透射边界进行计算的结果有较高的精度。

3 数值算例

3.1 有限元计算模型及参数选取

计算土体的有限元模型如图1所示，边界条件为：右端自由边界，下端固定边界，左端对称边界。

图1 计算土体的有限元模型

模型以轨道中心线为对称轴，沿对称轴方向取50m，垂直于轴方向取100m。数值模拟采用ANSYS有限元计算软件，时间步长采用0.002s，单元为四结点等参元，阻尼采用Rayleigh阻尼，土体的具体参数详见文献[1]，计算方法为Newmark-β法。通过数值分析得到不同距离、不同深度处的加速度响应。将数值模拟的结果与文献[1]的实测值进行对比，研究有限元计算的可靠性、计算精度及振动的传播规律。

在有限元数值模拟中，激励为文献[1]的三种工况下的测点1测得的竖向加速度实测值，分别为G1、G2和G3（见图2），对应的列车时速分别为120km/h、144km/h和151km/h。

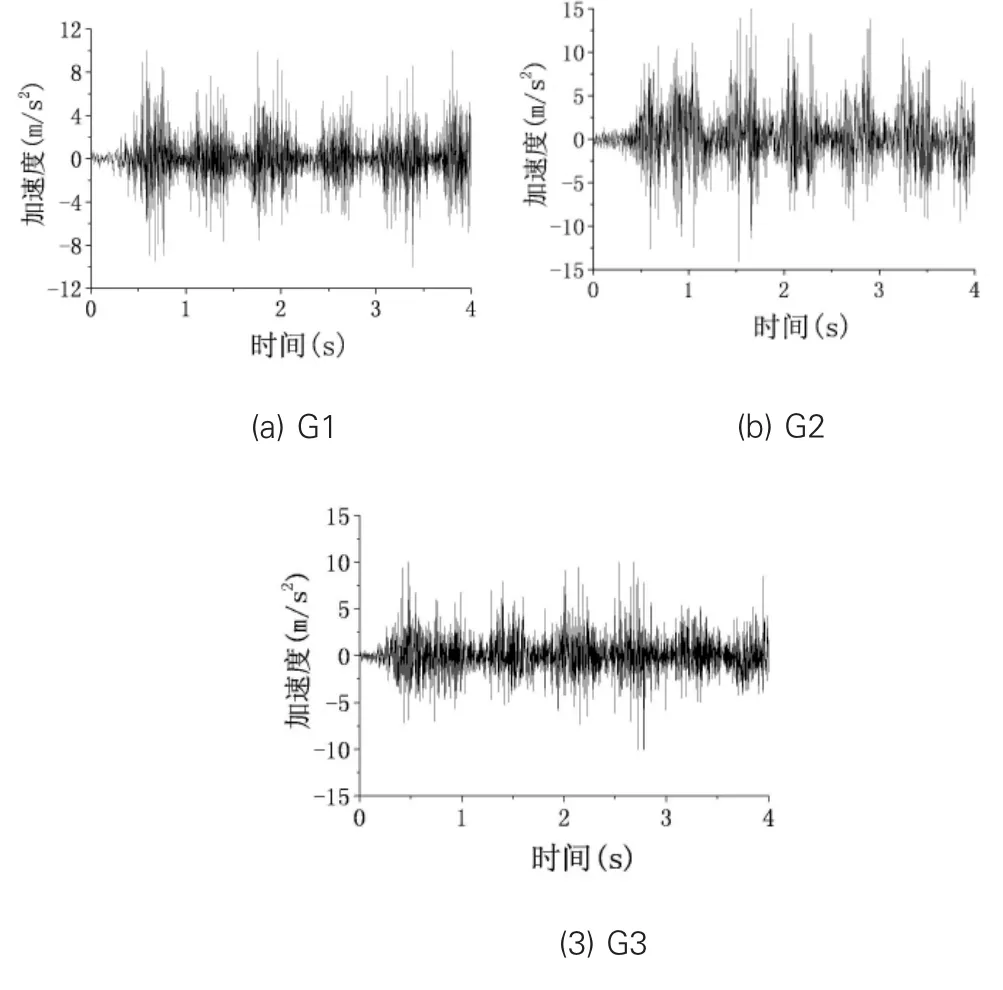
图2 三种工况输入的加速度时程激励

3.2 地表竖向振动数值计算结果与实测值对比

图3为G1离振源距离为5m、10m、20m、30m、50m处各点竖向加速度时程图及1/3倍频谱图。

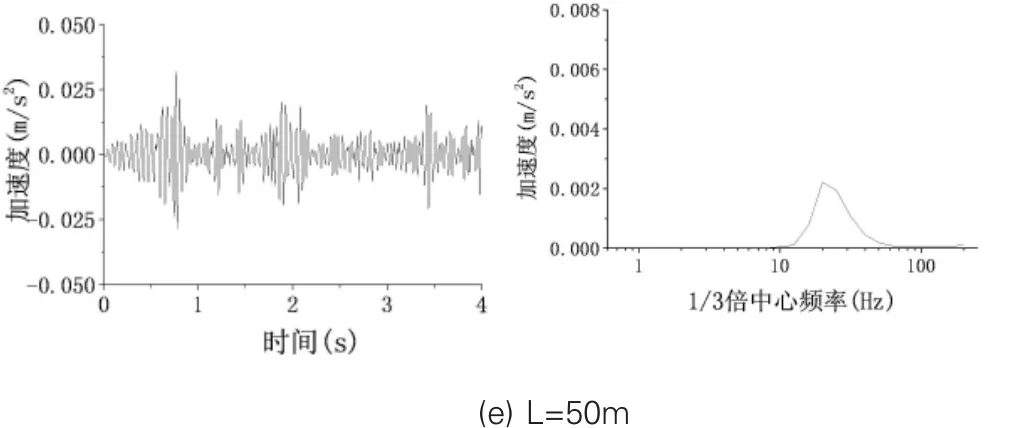
图3 G1地表不同距离处竖向加速度时程及1/3倍频谱

从图3中看到，地面振动的频率主要分布在10～120Hz之间，加速度峰值变化与振源距离成反比；其主频也与振源距离成反比，但减小幅度不大；竖向振动中的高频成分会在振动的传播过程迅速衰减。

图4为3种工况下地表竖向加速度振级的计算结果与文献[1]的实测值对比，从图中可以看出加速度振级会离振源距离的增加而相应减小。有限元计算值与实测值趋势较一致，说明土体参数及计算方法的合理性。

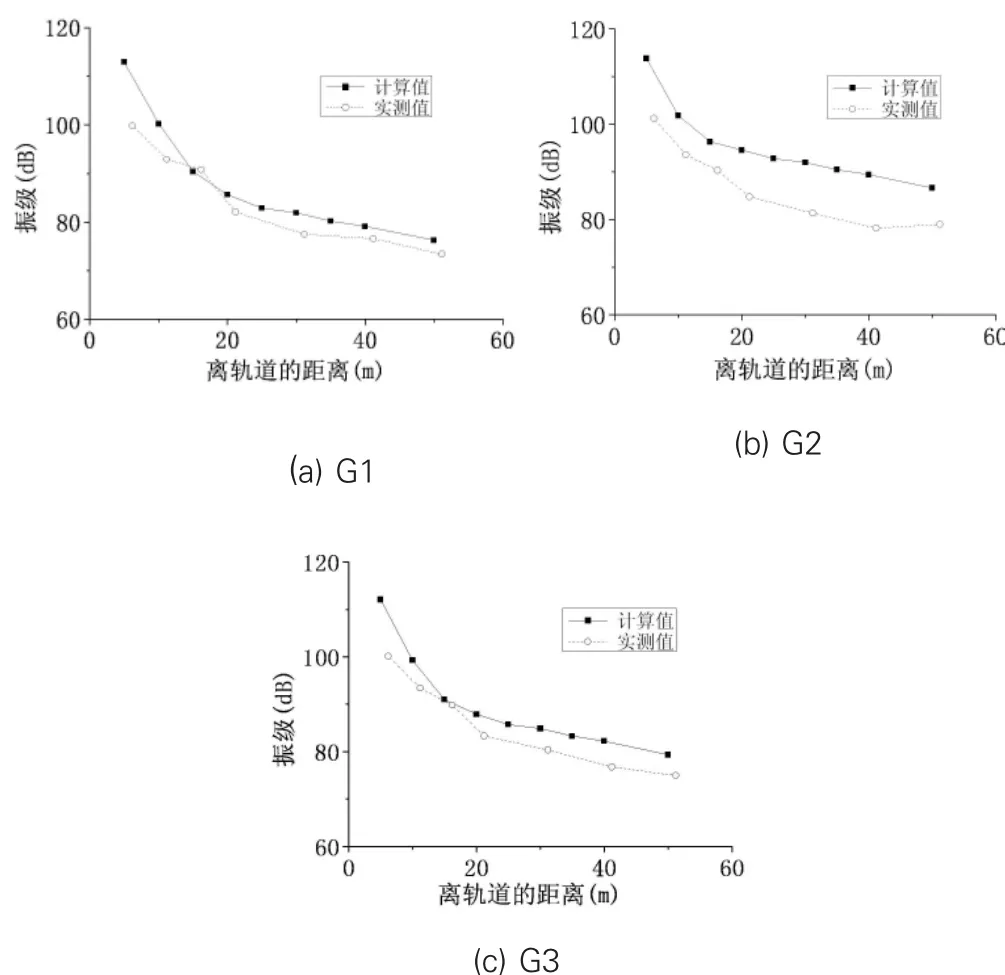
图4 地表加速度振级计算值与实测值的比较

3.3 阻尼对竖向振动的影响

为了研究阻尼对振动传播的影响，模拟计算选取的阻尼比为0.05、0.04、0.03、0.02 。图5中L表示距离轨道水平距离。

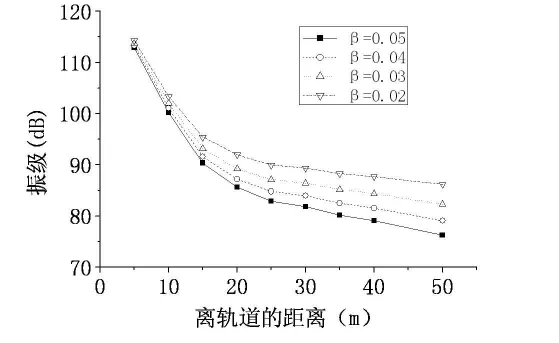
图5 不同阻尼比竖向振动沿地表的传播

图5分析可知，阻尼比相同时，随着水平距离的增加，土体的加速度振级衰减速度会先快后慢再逐渐趋于平缓；而如果离轨道水平距离相同，加速度振级衰减会随着阻尼比增大而加快。

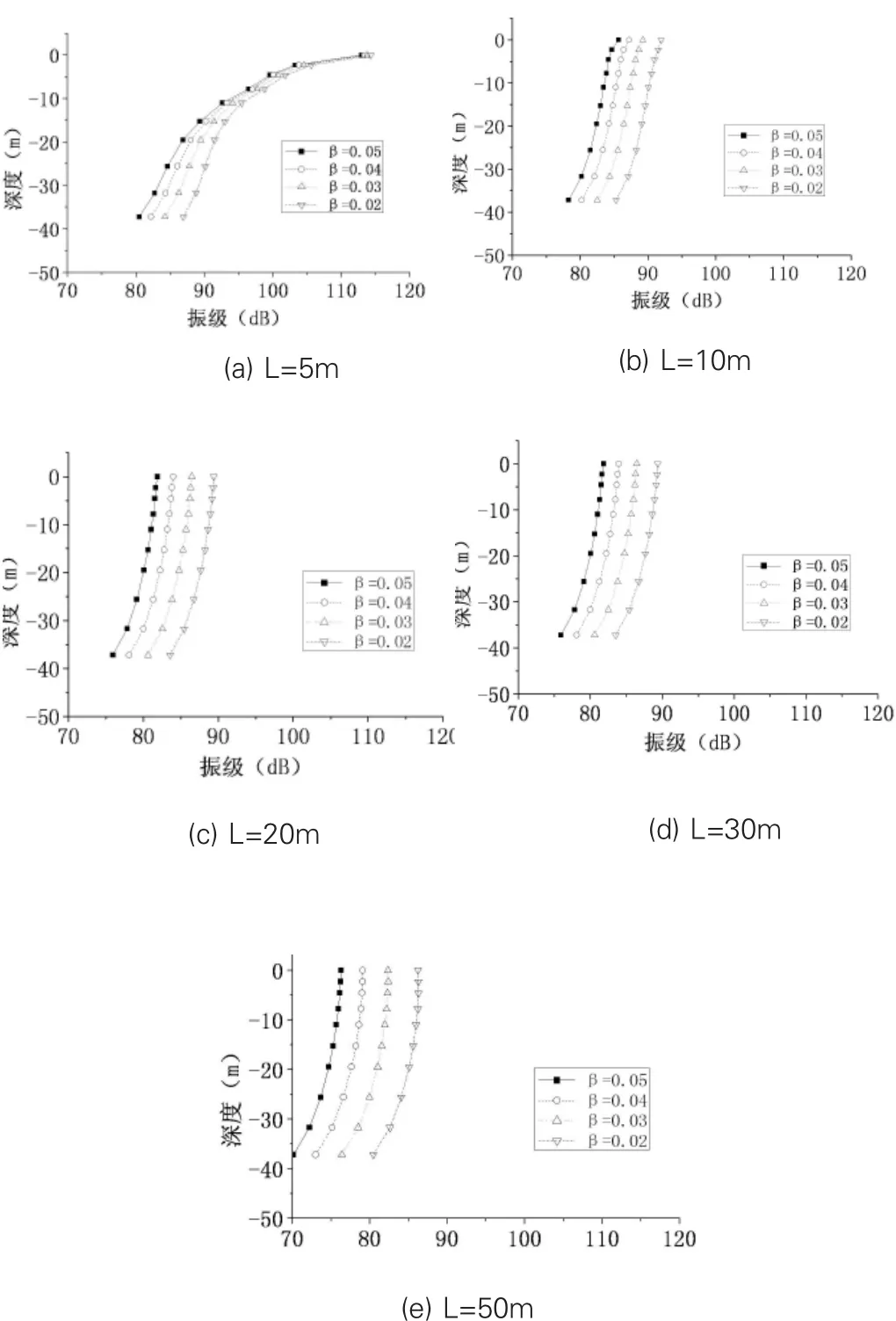
图6 不同阻尼比竖向振动沿深度的传播

由图6可知，当L和阻尼比固定时，随土体深度的增加，加速度振级衰减会先快后慢，再快；若L增加，加速度振级沿土体深度的衰减会比较缓慢；当L和土体深度相同时，加速度振级会随着阻尼比增大而衰减加快。

3.4 竖向振动沿土体深度的变化规律

现对3种不同工况下不同深度处土体的竖向加速度振动进行数值计算，分析竖向振动的相关变化规律。

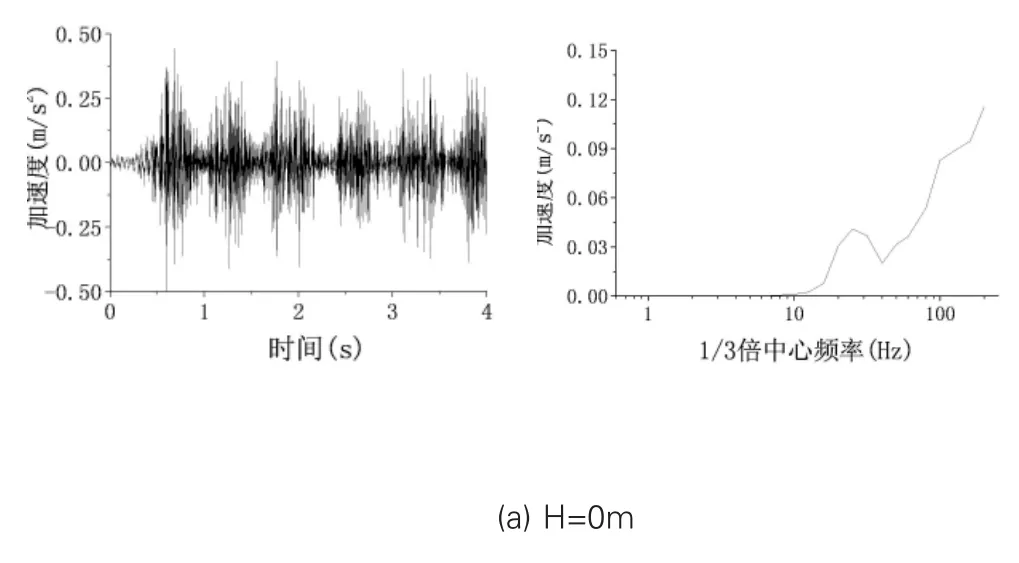
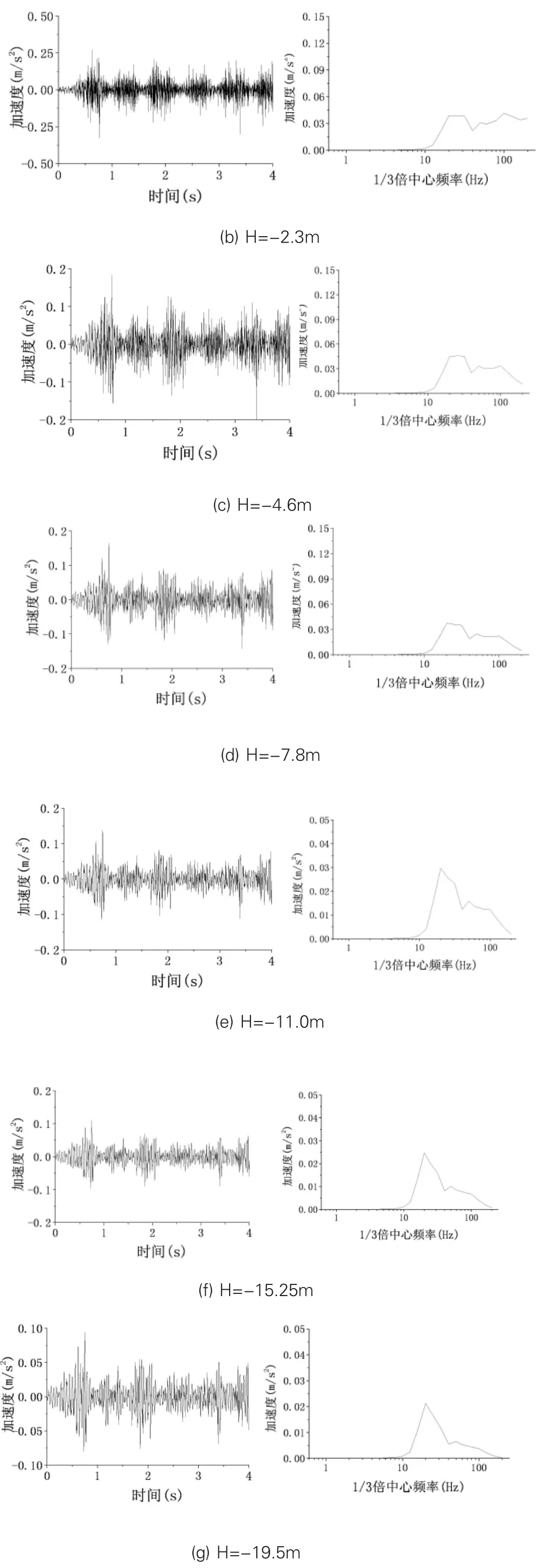
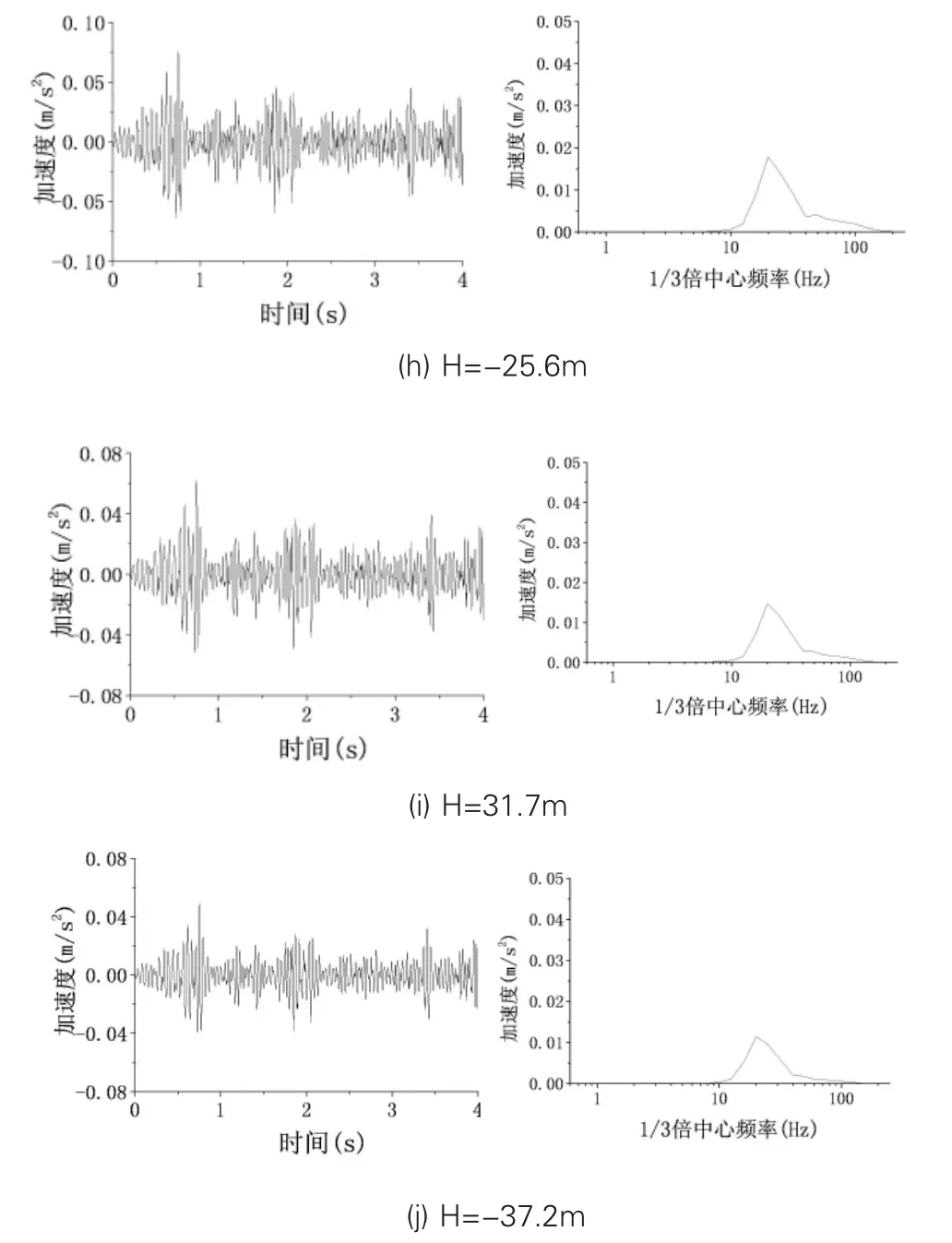
图7 L=10m处不同深度时竖向振动加速度曲线及1/3倍频谱（G1）

图7中为G1距离轨道10m时不同深度处的竖向加速度振动时程曲线及1/3倍频谱，可以看出竖向加速度峰值随着深度的增加而逐渐减小，并且在1/3倍频谱中，高频分量随深度衰减现象十分明显。

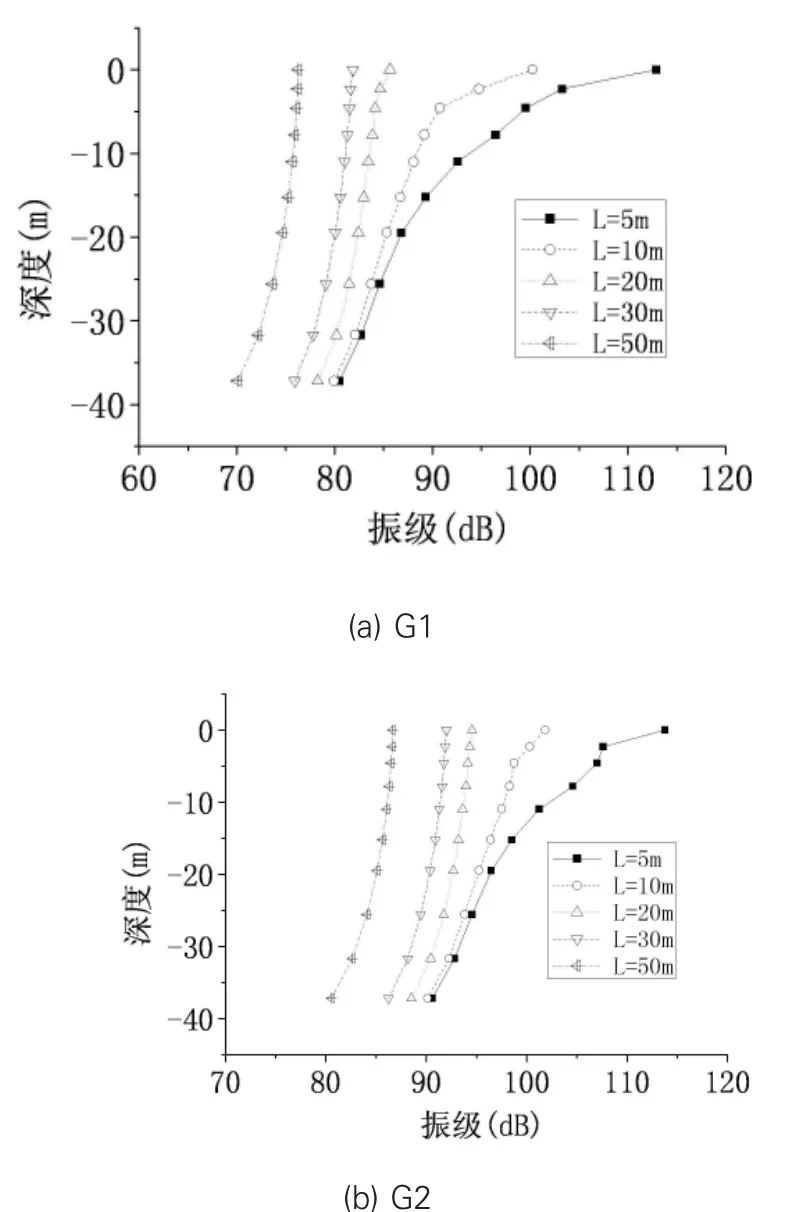
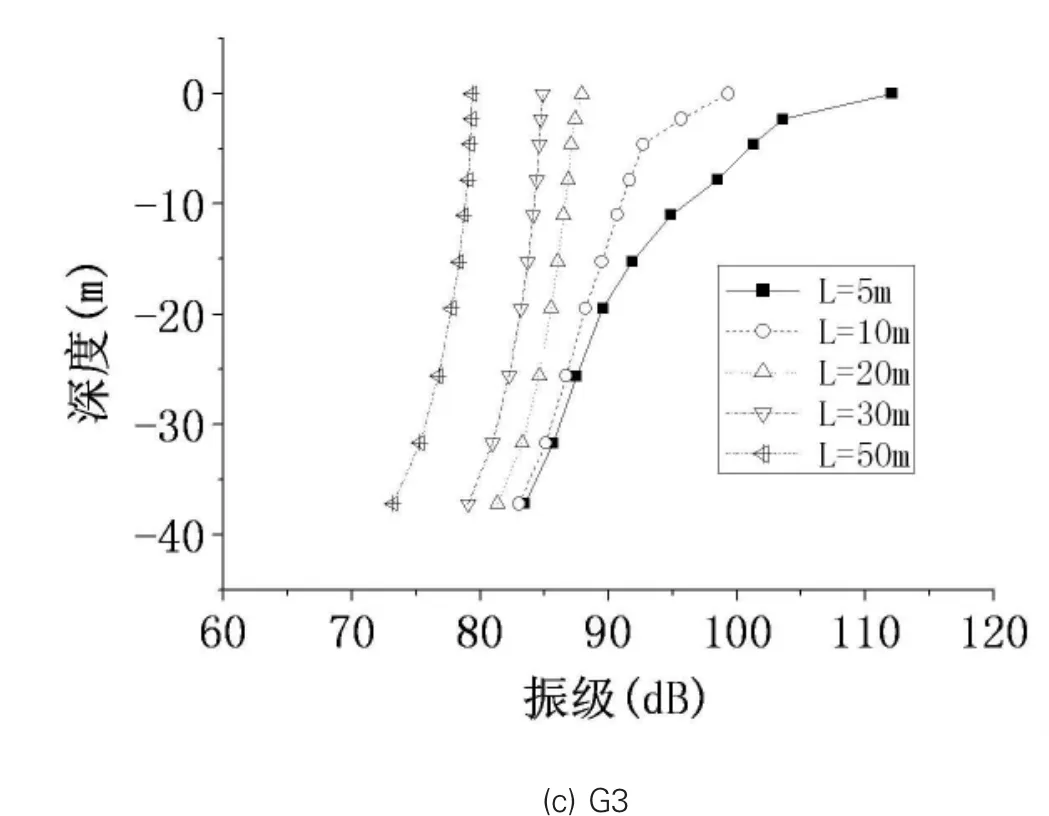
图8 水平距离不同时竖向振动沿土体深度的传播

图8可以看出：竖向振动衰减速度由近及远变慢；在距轨道较近处，衰减随深度增加速度减缓；在距轨道较远处衰减随深度的增加迅速增加。

4 结论

本文利用有限元法研究了列车运行引起的竖向振动在土体中传播规律，并对有限元模型、计算参数等进行了分析。还将数值分析结果与文献[1]的实测值进行了对比，结论如下：

（1）本文选取的有限元模型有效、参数合理，模拟结果与实测值吻合较好。

（2）由列车运行引起的地表竖向振动的频率集中在10～120Hz之间，它和主频、振级都随着距离振源距离的增大不断减小，并且随振动的不断传播，高频成分迅速衰减。

（3）竖向加速度峰值随着土体深度的增加逐渐变小，在1/3倍频谱图中，高频竖向振动会随着深度增加明显衰减；竖向振动衰减的幅度在距离轨道较近时更加明显。

（4）阻尼比相同时，随着水平距离的增加，土体的加速度振级衰减速度会先快后慢再逐渐趋于平缓；而如果离轨道水平距离相同，加速度振级衰减会随着阻尼比增大而加快。

[1]葛勇.无碴轨列车运行引起的环境振动及舒适度研究[D].重庆：重庆大学,2010.

[2]王常晶.列车移动荷载作用下地基的动应力及饱和软粘土特性研究[D].杭州：浙江大学,2006.

[3]申跃奎.地铁激励下振动的传播规律及建筑物隔振减振研究[D].上海：同济大学,2007.

[4]Kurzweil,L.Ground-borne noise and vibration from underground rail systems[J].Journal of sound and vibration,1979.，66(3):363-370.

[5]Takemiya,H.,A.Fujiwara.Wave propagation/impediment in a stratum and wave impeding block(WIB)measured for SSI response reduction[J].Soil Dynamics and Earthquake Engineering,，1994.，13(1):49-61.

[6]Melke,J.Noise and vibration from underground railway lines:proposals for a prediction procedure[J].Journal of sound and vibration,1988.，120(2):391-406.

[7]Ahmad,S.,T.Al-Hussaini.Simplified design for vibration screening by open and in-filled trenches[J].Journal of Geotechnical Engineering,1991.，117(1):67-88.

[8]Jones,C.J.C.,Thompson,D.J.,Petyt,M.Studies using a combined finite element and boundary element model for vibration propagation from railway tunnels[C].QQProceedings of the Seventh International Congress on Sound and Vibration,Garmisch-Partenkirchen,Germany,July 4-7,2000.Germany,International Institute of Acoustics and Vibration(IIAV),2703-2710.

[9]杨永斌.高速列车所引致之土壤振动分析[D].台湾：台湾大学，1996.

[10]Yang,Y.,H.Hung.A parametric study of wave barriers for reduction of train-induced vibrations[J].International Journal for Numerical Methods in Engineering,1998.，40(20):3729-3747.

[11]刘金.地铁振动在土层中的传播特性研究[D].沈阳：沈阳工业大学,2009.

[12]和振兴.板式无砟轨道交通引起的环境振动研究[D].成都：西南交通大学,2008.

[13]夏禾,吴萱.城市轨道交通系统引起的环境振动问题[J].北方交通大学学报,1999.，23(004):1-7.

[14]谢伟平,兰洋.2.5维有限元法分析地铁列车引起的地基振动[J].武汉理工大学学报,2009(013):78-82.

[15]陶连金,张丁盛.地铁诱发地面运动的衰减规律的研究分析[J].世界地震工程,2003.，19(001):83-87.

[16]李晓霖.地铁诱发振动对地面以及地上结构的影响规律研究[D].北京:北京工业大学,2003.

[17]He,X.Study of vibration effects of underground trains upon surrounding environments [J].Advances in Structural Engineering,1995，3:116-122.

[18]崔正翔,嵇正毓.地铁隧道振动对地面环境影响预测的探讨[J].噪声与振动控制,1996(001):9-14.

[19]Forrest,J.,H.Hunt.Ground vibration generated by trains in underground tunnels[J].Journal of sound and vibration,2006.，294(4-5):706-736.

[20]沈霞.地铁振动计算分析中的若干问题研究 [D].上海：同济大学,2005.

[21]吴良芝.结构有限元的修正解 [J].固体力学学报,1981.，2(4):457-467.

[22]沈聚敏,周锡元,高小旺,等.抗震工程学[M].北京：中国建筑工业出版社.，2000.