求解五对角和九对角线性方程组的追赶法

续小磊，马 丁 (宁夏大学数学计算机学院，宁夏 银川 750021)

求解五对角和九对角线性方程组的追赶法

续小磊，马 丁 (宁夏大学数学计算机学院，宁夏 银川 750021)

利用追赶法求解三对角线性方程组的思想，推导出求解五对角和九对角线性方程组的追赶法。此方法不必选主元、计算量小、存储量小、避免了中间结果数量级的巨大增长和舍入误差的严重积累、运算速度快而且Matlab程序编写也较为简单。

追赶法；稀疏矩阵；五对角矩阵；九对角矩阵

求解偏微分方程经常用到差分法，比如五点差分和九点差分，这样的差分格式最终是以线性方程组的形式出现，而这些方程组的系数矩阵就会是五对角或者九对角矩阵[1-4]。对于线性方程组的求解主要有直接法和迭代法，最基本的直接法是高斯消去法，但是高斯消去法计算量比较大，而且由于对角矩阵含有大量的0元素，如果使用高斯消去法将会对计算机的存储造成极大的浪费，而且需要较长的计算时间。而迭代法一般也需要足够的迭代次数才能达到所需要的精度，甚至有时候发散，而且程序编写复杂，不易实现。在这种情况下，使用追赶法求解线性方程组就比较理想[5-6]。下面，笔者将利用追赶法的思想来求解五对角和九对角线性方程组。

1 五对角线性方程组追赶法的推导

设有如下五对角线性方程组：

(1)

将其简记为：

Ax=f

(2)

若五对角矩阵A满足如下条件：

(1)ai,ei≠0,i=1,…,n-2;bi,di≠0,i=1,…,n-1；

(2)|c1|>|d1|+|e1|; |c2|>|b1|+|d2|+|e2|; |ci| > |ai-2| + |bi-1| + |di| + |ei|,i=3,…,n-2;|cn-1|>|an-3|+|bn-2|+|dn-1|; |cn|>|an-2|+|bn-1|；

那么矩阵A存在唯一的Crout分解，其分解形式为：

A=LU

(3)

式中，L为下三角矩阵；U为上三角矩阵，具体形式如下：

(4)

利用矩阵的乘法，对照式(3)容易得出：

si=ai,i=1,2,…,n-2;m1=b1;mi=bi-si-1pi-1,i=2,3,…,n-1;

l1=c1;l2=c2-m1p1;li=ci-si-2qi-2-mi-1pi-1,i=3,4,…,n;

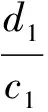
将方程组Ax=f改写为LUx=f，新的方程可分解成下面的形式：

(5)

综合分解与求解的过程，可得到解五对角方程组的追赶法。类似于三对角方程组，它也分为追和赶的过程，其中计算yi的过程称之为追的过程，计算xi的过程称之为赶的过程。

首先通过解方程组Ly=f求得yi的值，即追的过程。将矩阵形式转化为方程组可得：

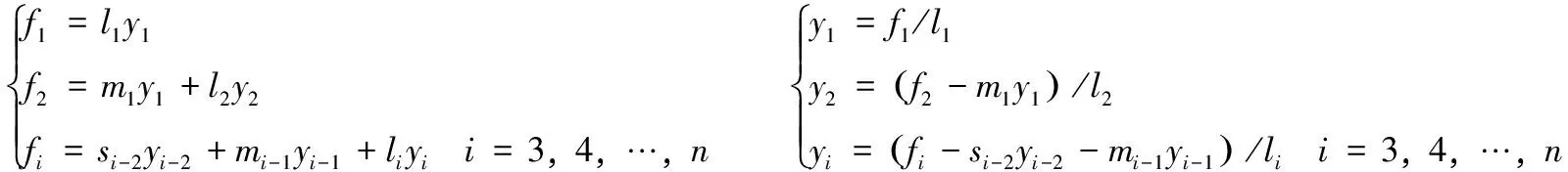
将si、mi、li的值代入即可求得yi的值。

现在可以通过解方程组Ux=y而求出xi的值，即赶的过程，由方程组Ux=y，可得：

最后将pi、qi的值代入即可求得xi的值。

2 九对角线性方程组追赶法的推导

设有如下九对角线性方程组：

(6)

简记为：

Ax=f

(7)

设此九对角矩阵A满足下列条件：

(1)ai≠0,i=1,…,n-4;zi≠0,i=1,…,n-3;hi≠0,i=1,…,n-2;bi≠0,i=1,…,n-1;di≠0,i=1,…,n-1;wi≠0,i=1,…,n-2;ui≠0,i=1,…,n-3;ei≠0,i=1,…,n-4；

(2)|c1|>|d1|+|wi|+|ui|+|e1|; |c2|>|b1|+|d2|+|w2|+|u2|+|e2|,|c3|>|h1|+|b2|+|d3|+|w3|+|u3|+|e3|; |c4|>|z1|+|h2|+|b3|+|d4|+|w4|+|u4|+|e4|,|ci|>|ai-4|+|zi-3|+|hi-2|+|bi-1|+|di|+|wi|+|ui|+|ei|,i=5,…,n-4,|cn-3|>|an-7|+|zn-6|+|hn-5|+|bn-4|+|dn-3|+|wn-3|+|un-3||cn-2|>|an-6|+|zn-5|+|hn-4|+|bn-3|+|dn-2|+|wn-2|,|cn-1|>|an-5|+|zn-4|+|hn-3|+|bn-2|+|dn-1|; |cn|>|an-4|+|zn-3|+|hn-2|+|bn-1|；

则A存在唯一的Crout分解，其分解形式为：

A=LU

(8)

式中，L为下三角矩阵；U为上三角矩阵，具体形式如下：

(9)

(10)

利用矩阵的乘法，通过式(9)可得：

si=ai,i=1,…,n-4;g1=z1;gi=zi-si-1pi-1,i=2,…,n-3;

t1=h1;

t2=h2-g1p1;ti=hi-si-2oi-2-gi-1pi-1,i=3,…,n-2;

m1=b1;m2=b2-t1p1;

m3=b3-g1o1-t2p2;mi=bi-si-3vi-3-gi-2oi-2-ti-1pi-1,i= 4,…,n-1;

l1=c1;

l2=c2-m1p1;l3=c3-t1o1-m2p2;l4=c4-g1v1-t2o2-m3p3;

li=ci-si-4qi-4-gi-3vi-3-ti-2oi-2-mi-1pi-1,i=5,…,n;

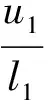
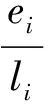
将方程组Ax=f改写为LUx=f，同前面求解五对角方程组一样，用追赶法求解九对角方程组也是分为追的过程和赶的过程，其中计算yi的过程称为追的过程，计算xi的过程称为赶的过程。

先解方程组Ly=f，即追的过程,可得：

(11)

则：

(12)

将si、gi、ti、mi和li的值代入式(12)即可求得yi的值。

再解方程组Ux=y，即赶的过程，可得：

(13)

则：

(14)

将pi、oi、vi和qi的值代入式(14)即可求得xi的值。

3 数值试验

例1[5]以如下一个n维九对角线性方程组为例，分别用高斯消去法和笔者推导的追赶法进行求解，比较2种方法的运算时间。在Matlab编程中，对于高斯消去法中的矩阵采用稀疏矩阵进行存储。

如表1所示，在取n=30,40,50,60时，分别用高斯消去法和追赶法求解了这个线性方程组，很明显能够看出，追赶法所需要的运算时间远小于消去法，而且这是在对高斯消去法中的矩阵利用稀疏存储之后的结果。

表1 消去法和追赶法运算时间的比较

4 结 语

将求解三对角方程组的追赶法推广到求解五对角和九对角线性方程组，这一推广提供了现成的求解五对角和九对角方程组的方法和程序，方便直接利用。通过一个九对角线性方程组的数值算例将追赶法和高斯消去法进行对比，数值试验结果表明，追赶法在运算量、存储量以及计算效率上均具有较大的优势。

[1]王礼广,蔡放,熊岳山.五对角线性方程组追赶法[J]. 南华大学学报(自然科学版),2008, 22(1): 1-4.

[2]王晶昕,薛静. 用五参数法求解拟五对角方程组[J]. 吉林师范大学学报(自然科学版), 2008, 29(2): 5-9.

[3]李文强, 刘晓. 追赶法并行求解循环三对角方程组[J]. 科技导报, 2009, 27(18): 90-93.

[4]陈志,高旅端. 求解大规模稀疏线性方程组的算法[J]. 北京工业大学学报, 2001(9): 262-265.

[5]李庆扬, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2008.

[6]蔡大用, 白峰杉. 高等数值分析[M]. 北京: 清华大学出版社, 1997.

[编辑] 洪云飞

O241.6

A

1673-1409(2013)25-0005-05

2013-06-17

续小磊(1986-)，男，硕士生，现主要从事偏微分方程数值解方面的研究工作。