GPS拟合高程精度浅析

高 云 张维宽 王 财

（1.青海省柴达木综合地质矿产勘查院 816000；2.青海省地质调查院 810012；3.青海省柴达木综合地质矿产勘查院 816000）

1 全球定位系统高程异常求解方法

1.1 勘探区GPS网概况

本文勘测区的全球定位系统网测试时间是2007年到2009年，使用的机器为Trimble5700 双频全球定位系统接收机，根据的是02《全球定位系统测量规范》中的要求进行测试，测试按照的是D和E级的形式布置网络。各个地方测试数据如表1

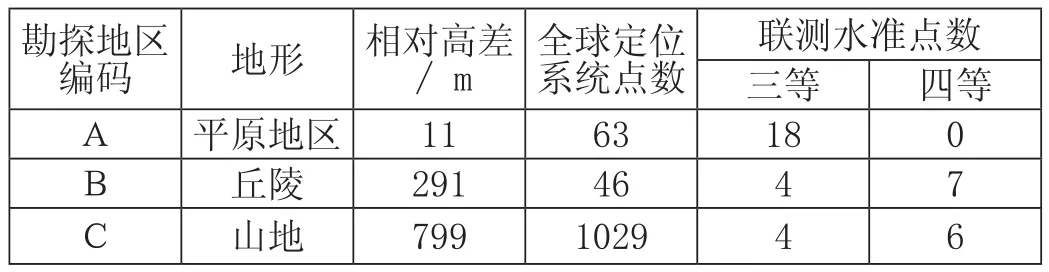
表1 各地区概况统计表

1.2 关于GPS的高程出现异常和变化求解

我们已经全面了解到，大地高用大写字母H表示，正常的高则用小写字母h表示，两者之间的关系如下

式中的H即大地高可通过全球定位系统测量得到，h则是由水准或三角高程测试得到，在根据前面的公式§=H-h即可得到高程异常值。

特别注意：ξ参考点高程异常。再根据式子Δξ=ξ- ξ,相对中部一点(参考点)计算的高程异常变化量可参考表 2。

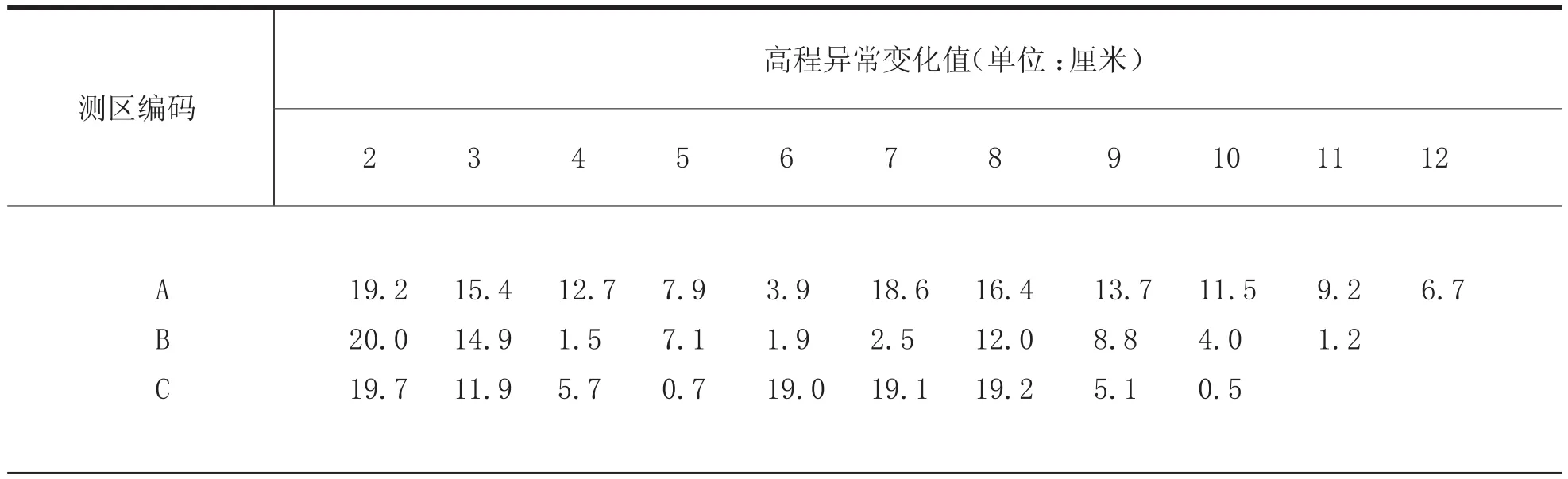
表 2 高程异常变量统计表

通过部分资数据加资料的统计分析, 平原地区覆盖区域,是大地之间的水准面相对比较平缓,变化范围在每千米4厘米上下; 丘陵地区尤其是梯田最为底部和丘陵上面部分, 是大地水准面有曲率显示, 其变化的范围每千米 7厘米上下; 在山区,地形地貌之间有很大的相似性，所以会对测试有一定影响，是大地水准面变化较大, 其变化范围为每千米 10厘米左右。结合三个地区的高程异常数据显示，其走向是东西较大, 南北较小。

2 GPS点正常高度求解方法

2.1 GPS点正常高求解方法

现假定有任意的一点，其平面坐标为n、m。那么高程异常即可用公式ξ=f(n, m) (公式3)表示，在高程异常的情况下，即只要知道已知地点那么可列出公式ξi=f(ni, mi)=Hi- Hγi（公式4）式中的Hi为已经知道的数据即高程值，Hγi为大地高，这些数据都可以通过全球定位系统测量得到。这里 f(n, m) 为与测区大地水准面相拟合的数学面, 取公式为以下表示f(n, m)=a0+a1n+a2m+a3n2+a5m5 (公式5)，特别注意的是: ai(i=0, 1,2, 3, 4, 5)拟合面系数。在已知高程异常的点上, 再依据公式4 及公式5 , 写出误差方程组的一般形式：V=AX+L,最后可通过公式x=-(ATPA)-1(ATPL) ，在这种情况下，各个点的高程异常值加可以求出来了而后在将数据代入公式1中，便能算出各点正常高

2.2 拟合点高程及检核点差计算

拟合的 GPS 高程及已知的水准高程进行相关比较, 求解公式是: V=H拟合- H水准, 三个测量地区中，每个测量的数据均有差别。

（1）关于拟合精度的计算

（2） 全球定位系统正常情况下的高较差与水准及三角高程的限差对比

根据目前关于水准及三角高程的相关规定，取全球定位系统点到最近的已知点距离，之后再算出限差进行对比仔细观察表4，不难发现，平地全球定位系统拟合后的高程精度,大概有百分之四十，达到了三等水准限差, 大半部分都能达到四等水准限差规定, 只有少数是以小部分超限, 这实际上已经很接近限差了，表4只例出了关于平原的数据统计。下把丘陵和山地的统计数据做简单的丘陵地统计为13点, 全球定位系统拟合后的高程精度有大概百分之三十二，达到三等水准限差, 全部达到等外水准限差的规定, 最后还有百分之八十五小于限差二分之一。山地统计 12 点, 全球定位系统拟合后的高程精度大概有百分之三十三点三，可以到达四等水准限差, 所有的都达到三角高程限差的相关规定。

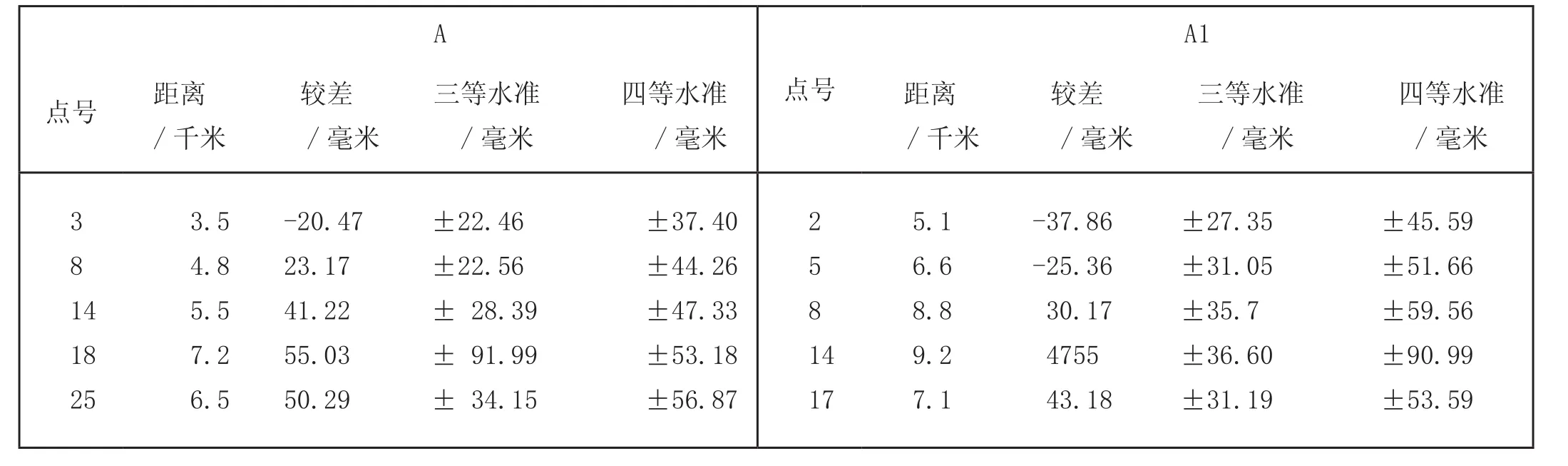
表4 全球定位系统在正常情况下的高较差与水准及三角高程限差比表

对于全球定位系统网，特别是已知水准点相对较少、实施起来难度较大的线路全球定位系统网，对于高程平差方法、方式的分析及探讨，不但能节省大部分水准测量的工作，还有很大的经济效益和发展潜力。受监测地区全球定位系统网, 应该要使用等级水准联测部分点,对GPS 网拟合求解正常高, 高程中误差, 平地±2.11cm,丘陵地±6.25cm,山地±13.55cm。另外，为了最大限度的提高全球定位系统正常的高精度, 需对椭球面进行精化及地理特征的相关性研究,特别是在丘陵地带及山区地带, 应该不断增加对地形及重力改正。

[1] 周忠谟.GPS 卫星测量原理与应用[M].北京:测绘出版社 ,2009（36）.

[2] 伍青云.GPS 高程拟合的方式及可靠性分析[J].中国煤田地质,20011(3).

[3] 赵庭安,田雪丰.矿区 GPS 高程拟合精度和可靠性研究[J].中国煤田地质,2010(3).