基于自动有限元建模的民机机翼结构布局优化

闫伟天 罗明强 刘 虎 武 哲

(北京航空航天大学 航空科学与工程学院，北京100191)

机翼设计是飞机总体设计中的重要组成部分，其中机翼结构设计又是机翼设计的重要内容.统计表明，每单位飞机结构重量的降低，能够降低约4.525单位的飞机总重［1］，更低的飞机总重意味着更低的油耗，对于民用飞机意味着更强的市场竞争力，因此在满足性能要求的前提下尽量降低结构质量就成为机翼结构优化的主要目标.由于机翼结构的布局也会对结构性能产生重要影响，因此有必要将布局优化纳入到结构优化中来.

随着CAD/CAE技术的发展，利用有限元分析技术能够在初步设计阶段快速对机翼结构进行分析，显著提高工作效率.将有限元技术应用到机翼结构布局优化中，关键问题之一就是在结构布局变化，尤其是纵、横向承力构件的数量变化后，如何实现有限元模型的自动生成［2-3］.目前的相关研究中，对上述问题都做了不同程度的简化以降低其复杂程度，其中文献［4-8］将横向承力构件的布置固定，只调整纵向承力构件的位置或数量;文献［9］中虽然考虑了纵、横向承力构件的数量变化，但有限元模型直接以纵、横向构件划分单元，导致网格尺寸过大，难以保证分析结果的精度.

本文针对民用飞机中典型的双梁式机翼结构，利用 Patran的 PCL(Patran Command Language)语言，实现了根据上、下蒙皮长桁数量和翼肋数量的变化自动进行有限元建模，并使建模精度能够满足初步设计的要求.然后利用Isight对Patran建模模块和Nastran求解模块进行集成，采用布局变量和剖面尺寸变量分离的双层优化策略，对机翼结构布局进行了优化.

1 机翼结构自动有限元建模

在关于机翼结构自动有限元建模的研究中，一般根据机翼几何外形和构件的位置及拓扑关系直接生成可用于有限元求解的文件.其中文献［10］针对的是可变形飞行器的机翼建模，不能应用到常规民用飞机上;文献［11］以机翼纵、横向构件直接划分有限元单元，导致单元尺寸过大，精度降低，同时该模型上、下蒙皮长桁数量必须相等，而实际工程中上蒙皮长桁数量一般多于下蒙皮长桁;文献［12］中有限元建模需要一定的人机交互操作，并未实现完全的自动建模，无法直接集成到优化流程中.

在初步设计阶段，为了实现快速迭代，对机翼进行静强度、刚度及稳定性分析只需对机翼翼盒进行分析，一般以线、面几何体来构建翼盒的几何模型，然后利用杆单元、梁单元和壳单元来构建其有限元模型.本文中机翼翼盒承力构件包括前、后梁、蒙皮、长桁和翼肋，其中翼肋为顺气流方向等间距布置，蒙皮长桁为沿弦向等百分比布置.以翼根处翼肋的前缘点为原点，以平行于机身轴线向后的方向为x轴正方向，以垂直于机翼平面向上的方向为y轴正方向，建立直角坐标系来构建机翼翼盒结构的几何模型(图1).

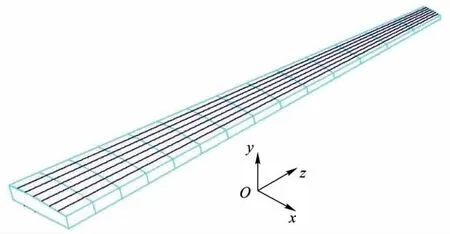
图1 机翼翼盒整体几何模型

下文将对机翼结构的有限元建模过程分为三步进行阐述，即分割再生成几何体、定义局部有限元单元和生成整体有限元模型.

1.1 分割再生成几何体

对于机翼结构的几何模型，梁缘条和翼肋缘条分别为其腹板所在平面与上、下蒙皮曲面的交线，且梁腹板和翼肋腹板的几何形状由其上、下缘条决定，同时长桁也与蒙皮曲面重合.因此根据梁、翼肋和长桁将上、下蒙皮分割成若干个曲面，每个曲面本身代表该部分的蒙皮，且该曲面的边可以描述位于该部分的翼肋缘条、梁缘条和长桁，进而由梁缘条和翼肋缘条去描述梁腹板和翼肋腹板(图2)，这些分割生成的几何体叠加在一起就能够完整描述整个机翼结构.以这些几何体的有限元单元为基础也可以构建整个机翼的有限元模型.

图2 机翼构件几何关系图

机翼长桁、翼肋的数量发生变化后，分割生成的曲面数量也会发生变化，Patran自动执行时对几何体的操作是通过其编号识别的，为了在操作这些曲面时不发生遗漏或错误，要求其编号具有一定的规律.在Patran中直接对蒙皮曲面进行分割操作，新生成的曲面编号混乱无序.而对曲线进行分割生成新曲线的编号是有规律可循的.因此本文先通过长桁对翼肋上、下缘条曲线进行分割，并根据生成曲线的展向和弦向站位对其进行编号，然后再由相邻翼肋上弦向站位相同的缘条曲线生成曲面，再对其进行编号即可得到编号规律的曲面，且该曲面与蒙皮必然重合.梁腹板曲面可以由分割后的翼梁上、下缘条曲线生成，并根据其展向站位进行编号.

各曲线和曲面的编号原则为

其中，i为翼肋的编号，由翼根向翼梢依次递增;j为长桁的编号，由前缘向后缘依次递增;Nrib为翼肋的数量;Nup为上蒙皮长桁的数量;Ndown为下蒙皮长桁的数量.

为保证编号的唯一性，要求上、下蒙皮长桁数量和翼肋数量均不超过50，这是符合实际情况的.按照上述原则完成的曲线、曲面编号见图3.

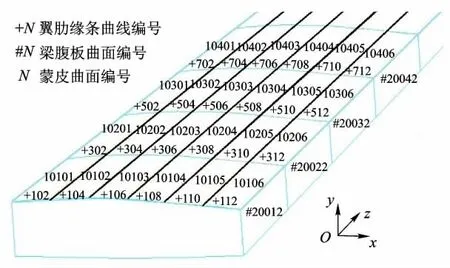
图3 各构件的曲线、曲面编号

对于翼肋腹板，上、下蒙皮的长桁数量不同导致分割翼肋上、下缘条生成的曲线数量也不相同，因此不能通过上、下曲线生成曲面的方式构建，而是直接由未分割的上、下缘条曲线生成.

1.2 定义局部有限元单元

为了保证有限元分析结果的精度，需要对上述生成的曲面和曲线进一步划分单元网格，然后根据单元所属的构件定义其单元属性.

对于蒙皮和梁腹板曲面，可以直接在其4条边上创建网格种子“Mesh Seed”，然后将其划分为四边形网格“QUAD4”.通过控制种子间距一致即可保证蒙皮与腹板相交处的网格划分一致.

对于梁缘条和长桁，与上述曲面的边重合，可以直接对曲面的边定义有限元单元.前面划分曲面网格时已在边上创建了种子，因此直接划分曲面的边生成的线网格与曲面网格必然一致.

为了使翼肋缘条与蒙皮曲面网格一致，通过将翼肋缘条与长桁的交点(也是蒙皮曲面的顶点)以“Associate”命令关联到翼肋缘条上，生成硬几何体“Hard Geometry”，然后对翼肋缘条曲线直接创建网格种子，硬几何体处必然生成种子，控制种子间距与蒙皮曲面一致，即可保证其相交处的网格划分一致.

对于翼肋腹板，其与蒙皮相交于翼肋缘条，与前、后梁腹板交于梁腹板曲面的边，直接根据翼肋缘条上和梁腹板曲面的边上的种子划分其网格，即可保证相交处的网格一致性.

局部网格划分完成后，各构件的网格关系见图4.根据1.1中的编号对所有分割生成的同类型几何体重复操作即可保证整个几何模型被划分了有限元网格.

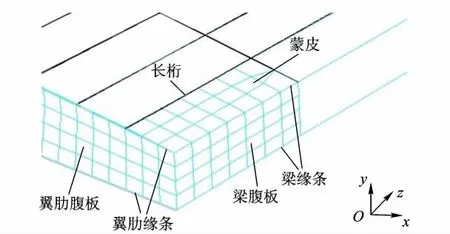
图4 不同构件网格划分一致

对于各构件的网格单元属性，腹板和蒙皮单元属性均为壳单元，长桁单元属性均为杆单元，缘条单元属性均为梁单元，其截面为“T”型.

1.3 生成整体有限元模型

在定义局部有限元单元的过程中，在其相交处产生了大量位置重叠的节点，为了将分散的局部有限元模型合并为一个完整的机翼结构有限元模型，可以通过合并相交处的重复节点，只保留最小编号的节点并删除多余节点的方式实现.

对于载荷与边界条件的定义，由于有限元单元划分的过程中涉及了单元与几何模型的关联关系，在Patran中将载荷与边界条件直接施加到几何模型上即可保证其施加到对应的单元节点上，避免了其定义受到单元节点编号变化的影响.

最终生成的机翼结构整体有限元模型见图5.以翼肋数为20，上、下蒙皮长桁数均为8为例，若以翼肋、长桁直接进行单元划分，则机翼有限元模型节点数为400，单元总数为1300;而本文构建的有限元模型在网格尺寸为0.15 m时节点数为3481，单元总数为6324，精度远高于前者.

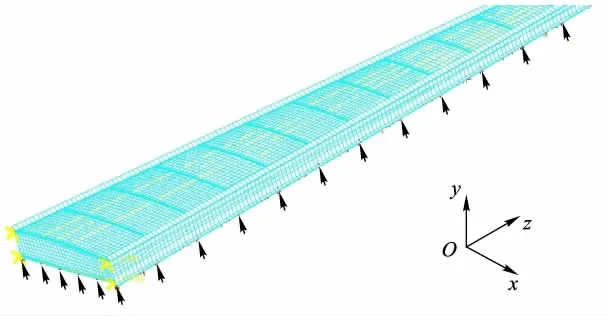
图5 机翼翼盒整体有限元模型

2 布局优化模型和优化策略

2.1 优化数学模型

2.1.1 优化变量

优化变量包括布局变量和尺寸变量.

布局变量有3个，分别为翼肋数量xrib，上蒙皮长桁数量xstrup，下蒙皮长桁数量xstrdown.

尺寸变量有12个，分别为上、下蒙皮长桁的截面积astrup，astrdown(m2);上、下蒙皮的厚度tskinup，tskindown(m);翼梁、翼肋腹板的厚度 tsparweb，tribweb(m);翼梁上缘条的高度和厚度hsparup，tsparup(m);翼梁下缘条的高度和厚度hspardown，tspardown(m);翼肋缘条的高度和厚度hribflange，tribflange(m).其中翼梁缘条的特征参数见图6.

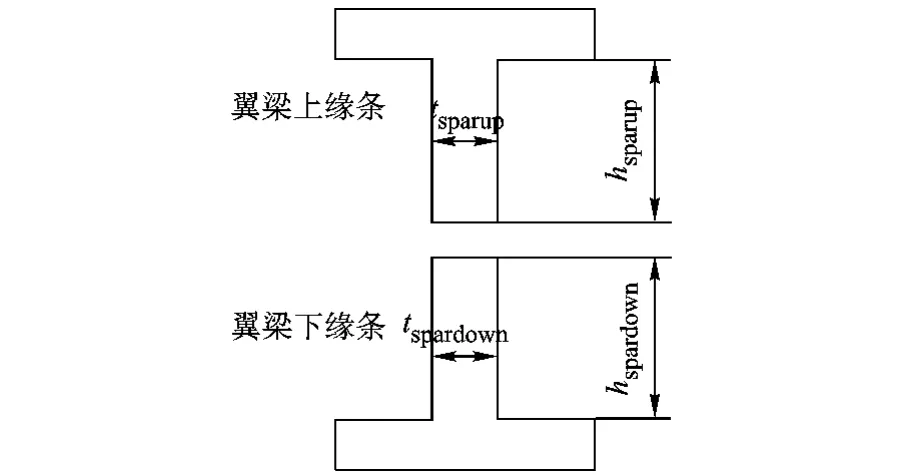
图6 翼梁上下缘条截面特征参数

2.1.2 目标函数

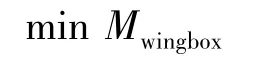
其中，Mwingbox为机翼翼盒质量(kg).

2.1.3 约束条件

其中，σb为最大正应力(MPa);［σb］为材料的抗拉强度，［σb］=450 MPa;σs为最大剪应力(MPa);［σs］为材料的抗剪强度，［σs］=250MPa;smax为机翼的最大位移，(m);lspan为机翼的半展长;e为机翼蒙皮失稳特征值.

2.2 优化策略

由于优化变量中既包括离散的设计变量(布局变量)，又包括连续的设计变量(尺寸变量)，对其同时进行优化会存在难以收敛、计算时间漫长的问题.

本文采用双层优化的策略，上层对布局变量进行优化，在布局固定的情况下，下层对机翼结构剖面尺寸变量进行优化，得出该布局下满足约束条件的最低质量，上层布局优化根据下层尺寸优化的结果对布局变量进行寻优，最终找到使机翼翼盒质量最低的布局即为最优布局.

上层布局优化采用多岛遗传算法(Multi-Island Genetic Algorithm)，该算法属于遗传算法的一种，适用于优化离散变量，并具有较强的全局寻优能力.

下层尺寸优化采用MMFD(Modified Method of Feasible Directions)算法，该算法是一种直接搜索的数值优化算法，适用于优化有约束问题，并具有快速获得最优点和在最优点能以较高精度满足约束条件的特点［13］.

优化流程见图7.

3 优化算例

3.1 算例说明

为了证明自动有限元建模和优化策略的有效性，参照某大型民用飞机的机翼外形尺寸，构建了机翼翼盒的几何 CAD模型，机翼半展长为14.2 m，根弦长6.1 m，根梢比为0.27，前缘后掠角28°，后缘后掠角13°，前梁位于弦向的15%处，后梁位于弦向的60%处，翼根处固支，机翼沿展向受到椭圆形分布的升力载荷.

机翼翼盒采用2A12高强度硬铝合金材料，密度2780 kg/m3，弹性模量69 GPa，泊松比0.33.

有限元模型中翼盒所受外载荷包括刚体机翼产生的气动力和翼盒结构质量引起的惯性力.

图7 机翼布局优化流程

3.2 优化结果

机翼初始布局为翼肋数量22，上蒙皮长桁数10，下蒙皮长桁数量10，机翼结构质量3616 kg.

最终的优化结果布局为翼肋数量19，上蒙皮长桁数7，下蒙皮长桁数5，机翼结构质量3 249 kg，相对于初始布局质量降低了10.1%.布局优化迭代过程见图8.

图8 机翼翼盒结构质量的优化过程

在布局迭代过程中，每种布局下均会得到一组最优尺寸值使结构质量最低，该值随布局迭代次数的相对变化见图9.

对于单纯的尺寸优化，结构减重主要依赖于结构件尺寸的减小和尺寸分布趋于合理，如变厚度、变截面等.由图9可知，在布局迭代过程中，每种布局得到的最优尺寸值总体变化趋势并不是单调减小，而是在某一范围内波动，且本文中的有限元模型均为等厚度、等截面构件.图8中机翼翼盒质量随布局迭代总体呈下降趋势，本文认为算例中的布局优化使结构减重的主要原因在于结构布局趋于合理从而减少了结构件即翼肋、长桁的数量.这也说明了结构布局的合理配置对于结构减重的重要性.

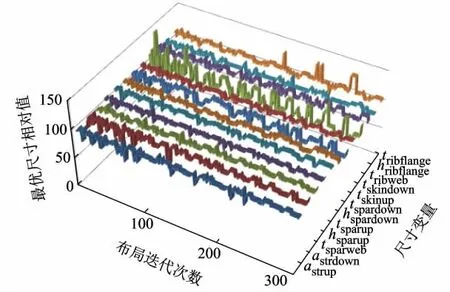
图9 布局迭代过程中最优尺寸值的相对变化

优化前后机翼布局对比见图10.

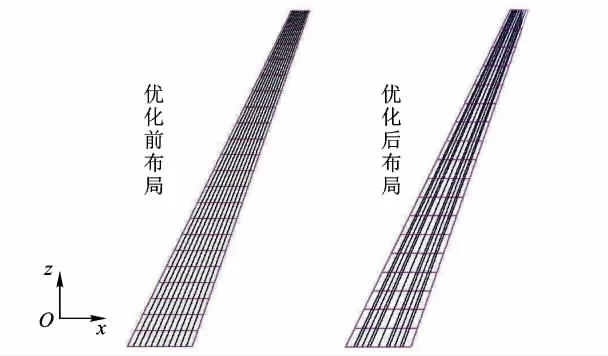
图10 优化前后布局对比

根据最终的优化结果可知，翼肋间距约为789 mm，这与统计数据的 800 mm［14］基本一致.同时优化结果中上蒙皮长桁数要多于下蒙皮长桁数，这与实际工程经验也是一致的.因为在弯矩载荷作用下上蒙皮受压，增加其长桁数量可以减小长桁的间距，有利于提高其抗压稳定性.

4 结束语

本文利用Patran的PCL语言，针对民用飞机的典型布局形式，实现了根据翼肋数量和上、下蒙皮长桁数量的变化自动进行有限元建模和分析，并将该有限元建模模块集成到机翼结构布局优化流程中.最后的算例结果表明，优化后的布局使机翼重量得到明显降低，且布局参数与实际工程经验基本吻合.这说明基于自动有限元建模的机翼结构布局优化能够为飞机初步设计工作提供一定的指导.

目前工作主要针对一种长桁和翼肋的布置形式，后续工作将增加机翼结构布局形式的种类，并通过机翼展向构件变厚度、变截面等方式进一步提高有限元建模精度.

References)

［1］ Shen J Y，Ferguson F.Weight reduction through optimal arrangement of force-carrying components within wing box structures［R］.AIAA-2004-4495，2004

［2］ Nawijn M，van Tooren M J L，Berends J P T J，et al.Automated finite element analysis in a knowledge based engineering environment［R］.AIAA-2006-947，2006

［3］王伟，常楠.飞机翼面结构多级布局优化设计思想及需要解决的问题［J］.飞机设计，2007，27(5):1-6 Wang Wei，Chang Nan.Multi-level optimization in wing structural configuration design and future research aspects［J］.Aircraft Design，2007，27(5):1-6(in Chinese)

［4］刘颖卓，张永存，刘书田，等.考虑复合材料蒙皮稳定性的飞机翼面结构布局优化设计［J］.航空学报，2010，31(10):1985-1992 Liu Yingzhuo，Zhang Yongcun，Liu Shutian，et al.Layout optimization design of wing structures with consideration of stability of composite skin［J］.Acta Aeronautica et Astronautica Sinica，2010，31(10):1985-1992(in Chinese)

［5］ Wang Wei，Yang Wei，Chang Nan.Integration shape and sizing optimization of composite wing structure based on response surface Method［J］.Transactions of Nanjing University of Aeronautics ＆ Astronautics，2008，25(2):94-100

［6］何林涛，万小朋，赵美英，等.布局优化和尺寸优化相结合的复合材料机翼优化设计［J］.中国机械工程，2008，19(17):2077-2080 He Lintao，Wan Xiaopeng，Zhao Meiying，et al.Composite aircraft wing structure optimization using combination of layout and sizing［J］.Chinese Journal of Mechanical Engineering，2008，19(17):2077-2080(in Chinese)

［7］王伟，赵美英，常楠.基于两相法的机翼结构几何优化设计［J］.飞机设计，2007，27(1):22-26 Wang Wei，Zhao Meiying，Chang Nan.Geometrical optimization of aircraft wing based on double-state technology［J］.Aircraft Design，2007，27(1):22-26(in Chinese)

［8］张仲桢，余雄庆，胡添元.飞翼式飞行器结构布局与构件尺寸的两级优化［J］.计算机辅助工程，2009，18(1):27-30 Zhang Zhongzhen，Yu Xiongqing，Hu Tianyuan.Two-level optimization on structural layout and component size of flying wing aircraft［J］.Computer Aided Engineering，2009，18(1):27-30(in Chinese)

［9］邓扬晨，詹光，高彤，等.飞机翼面结构布局综合设计方法研究［J］.飞机设计，2004(2):28-36 Deng Yangchen，Zhan Guang，Gao Tong，et al.Analysis and synthesis based aircraft wing structural layout study［J］.Aircraft Design，2004(2):28-36(in Chinese)

［10］ Skillen M D，Crossley W A.A matlab-based object-oriented process architecture for rapid generation of unconventional wing finite element models［R］.AIAA-2008-2160，2008

［11］罗明强，冯昊成，刘虎，等.机翼结构有限元的快速建模及自动化调整［J］.北京航空航天大学学报，2011，37(6):680-684 Luo Mingqiang，Feng Haocheng，Liu Hu，et al.Rapid wing structural finite element modeling and automated adjustment［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37(6):680-684(in Chinese)

［12］邓扬晨，廖家驹，章怡宁，等.面向设计的飞机翼面结构有限元自动建模技术［J］.飞机设计，2002(1):9-13 Deng Yangchen，Liao Jiaju，Zhang Yining，et al.Design-oriented finite element auto-modeling to aircraft wing structures［J］.Aircraft Design，2002(1):9-13(in Chinese)

［13］ Dassault Systèmes.Isight 4.5 Component Guide［M］.USA:Dassault Systèmes，2010:621-623

［14］王宝忠.飞机设计手册第10册:结构设计［M］.北京:航空工业出版社，2000:410-411 Wang Baozhong.Aircraft design manual vol 10-structure design［M］.Beijing:Aviation Industry Press，2000:410-411(in Chinese)