基于改进GA的柔性作业车间分批调度优化
刘 炀,熊俊西,程 晨,彭 骏
Liu Yang, Xiong Junxi, Cheng Chen, Peng Jun
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
0 引 言
作业车间生产调度是企业从大批量“推动式”生产迈向小批量“拉动式”生产的重要环节[1],对该问题的研究需结合实际的生产环境,才能真正实现理论研究的实用化。柔性作业车间调度问题[2](FJSP)释放了工序的资源约束,是传统车间调度问题[3](JSP)的重要扩展,近年来成为作业车间调度的研究热点[4]。然而,实际环境下不仅要解决机床分配问题和工序调度问题,而且要对各工件划分理想的生产批次和批量。另外,由于增加了批量分配子问题,使算法的设计过程和问题的值域空间都更加复杂,求解难度也会进一步增大。因此,对柔性作业车间分批调度问题(Flexible Job-shop Scheduling with Lot-splitting Problem,FJSLP)的研究具有重要的实践价值和学术意义。
目前,分批调度问题因其复杂性较高,通常采用启发式方法求解[5-6]。该方法按照对子问题的处理方式分为分步法[7]和集成法[8]。分步法将复杂问题划分为几个子问题分别求解,虽然可以降低计算难度,但获得的解只能保证各独立部分达到最优,不能体现整体最优,缺乏一定的说服力。集成法求解是将复杂问题统一考虑,其难点主要有两点:一是面对大规模值域如何寻优;二是编码和解码过程中如何表达模型中复杂的子批量工序排列。鉴于此,文中基于集成法思想将初始群体采用平衡设备负荷原则优化,设计工件交货期越早越优先加工的子批工序排序方法,对编码和解码过程同时改进,并采用遗传算法求解,取得了较好效果。
1 问题描述
FJSLP可描述为:生产多个不同种类的产品,各产品具有独立的工艺顺序和生产批量,且产品的工序存在多种加工设备。调度目标是:为每种工件确定合适的批量;为工件的各道工序确定合适的加工机器;为每台机器分配合适的工件加工顺序,使得系统总目标达到最优。问题通常基于如下假设:1)产品的工序事先确定;2)每道工序的加工时间及批次启动时间确定;3)加工过程中机器不因为人为和非人为的因素而停滞;4)各工件任何时刻都有可能被选择加工。
同时,具有如下约束条件:1)工艺顺序约束,同一批次工件的工序只有在上一道工序完成之后才能继续加工;2)加工资源约束,同一台机器在完成一个批次工件后才能加工另一批次工件;3)子批数量约束,工件的任一子批量都不能大于工件的总加工数,且各子批量之和为工件总加工数;4)子批启动约束,同一台机器相邻加工工件,同批次内加工无批次启动时间,不同批次则必须有批次启动时间。综上所述,FJSLP具有以下两个特征:1)继承FJSP存在的并行机和多功能机;2)强调对同种工件的子批工序的排列。基于以上描述,给出以下最短加工时间的数学模型和相关参数解释。
式中,Ei,j,k,m为工件i的子批j的工序k在机器m加工的完工时间;Si,j,k,m为工件i的子批j的第k道工序在机器m上的开始加工时间;ti,j,k,m为工件i的子批j的第k道工序在机器m上的加工时间;ti,j,k k′,m为机器m上相邻工序k与k′的批次启动时间;li为工件i的子批数;ni,l为工件i的第l子批的子批量;Ni为工件i的总加工数量;T为批次启动时间,为一常数。
模型中,式(1)表示调度目标为最小化工件的最大工序完工时间;式(2)~式(5)分别表示问题的工艺顺序约束、加工资源约束、子批启动约束和子批数量约束。
2 分批调度算法
2.1 编码设计
采用矩阵编码方式,将问题分解为工件编码区、批量编码区和工序编码区。工件编码区行数为工件的子批数和,列数为1,数值表示工件种类;批量编码区数值为各子批的工件加工数量;工序编码区表示工件各子批的加工工序,列数为最大子批工序数,列号为工件工序号,矩阵数值表示工序对应的加工设备,若工件工序数小于子批最大工序数,则用“0”补充“虚工序”,即该工序不安排加工设备。矩阵A即为对应表1工件信息的一个编码。
此编码方式相比染色体向量编码[9]问题信息表达更加直接,易于实现算法过程。

表1 工件信息表
2.2 算法详细描述
2.2.1 初始染色体优化
采用平衡设备负荷规则为工序安排加工设备,即工序选择当前累计负荷与工序负荷之和最小的设备,并将各子批排列成可执行的调度方案,进而获得质量较优的染色体。以染色体A为例,算法具体实现过程及中间解如下。
算法——工件分批排序算法。
步骤1:根据交货期设定工件i优先级,交货期越早,优先级越高;
步骤2:随机生成初始种群,基于工件加工优先级,以子批量小的优先加工原则设定工件子批排序优先级;
步骤3:依据子批优先级为工件i的工艺规程Pi选择当前累计负荷与加工负荷之和最小的设备,直到所有工序都被安排;
步骤 4:在模型约束式(2)、式(3)下,排列各批次工序并获得优化染色体。
表2为工件子批加工信息及设定的工件、子批排序优先级等;表3为设备安排子批工序过程的累计负荷及对应的子批工序,表中“1.1.3”表示工件1第1个子批的第3道工序在第1台设备上加工;子批顺序指为工序安排加工设备的顺序,由子批按照其工艺规程排列,主要为了避免工件太过集中导致makespan[10]增加。A′为平衡机器负荷后的优化染色体。经算法 1,初始随机染色体优化为目标较优染色体。图1为A′对应的时间甘特图。

表2 工件子批加工信息及排序优先级
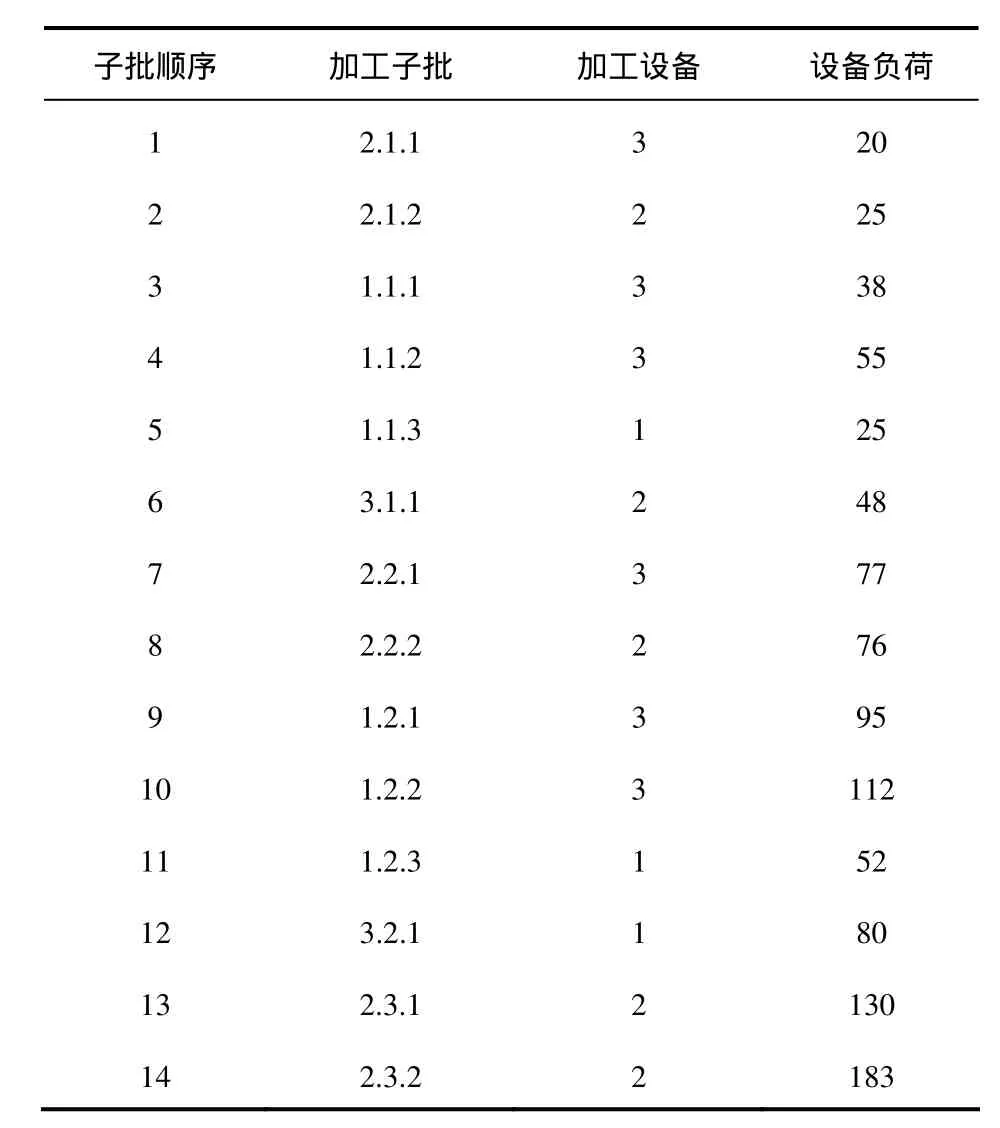
表3 设备负荷及加工工序
2.2.2 染色体解码
解码是将一个确定的编码按照设定的排列规则转换成一个调度方案并计算调度目标的过程。设备前工件采用最短完工时间原则排序,即在模型约束式(2)、式(3)下同一台设备前的工件,工序号小的工件进行前移,工序号大的工件后置。
算法2——染色体解码算法。
步骤1:提取染色体表示的工件子批量ni,l和工件工序集pi对应的加工设备集mi;
步骤2:计算各子批工序加工时间ti,j,k,m×ni,l;
步骤3:结合工序批次启动时间,以算法1的排序结果排列各设备前的工序;
步骤4:设工件i的第j道工序为pi,j,并设i=1,j=1;
步骤5:j′=j+1,若同台设备上的工序pi,j开始加工时间≥pi,j′的完工时间,转步骤 6,否则,转步骤7;
步骤6:在pi,j的紧前工序pi,j-1和pi,j′的紧后工序pi,j′+1满足模型约束式(2)、式(3)下,将工序pi,j和pi,j′分别前移、后置一次,否则,立即停止并返回步骤5;
步骤7:重复步骤5、步骤6直到设备工序全部被比较;
步骤8:i=i+1,j=1,返回步骤 5,直到不同工件全部被比较;
步骤9:算法结束,获得新的调度方案。
以A′为实例,经解码算法,获得新的调度方案,时间甘特图如图2所示。
2.2.3 染色体交叉与变异
遗传算法的染色体交叉与变异的实际应用一直是个难题,交叉后要确定工序在哪台设备上加工、工件的批次和工序的排列顺序。考虑到文中染色体在问题中表现的实际意义,交叉后可能会产生过多的不可行解,而重置或剔除这些不可行解会直接导致算法效率降低。因此,染色体交叉后既要保证解的更新,又要保证新的染色体在问题可行域内。模型受设备平衡负荷制约,算法1和算法2已经对工序进行工时和负荷的较优排列,文中设计局部交叉策略仅对批次、批量与设备进行更新。
设染色体A和A′为不同的问题编码,染色体总行数为n,交叉后生成染色体C。交叉时,首先随机确定染色体A交叉区的行号k和行数x并保证k+x-1 变异策略采取以一定概率替换交叉区的方式,为保证变异的合法性,随机选择一个非变异染色体作为替换染色体。 FJSLP模型可行域范围明显较FJSP大得多,因此,问题求解最大困难在于如何搜索到较优解。鉴于此,在初始化染色体后,首先对染色体进行目标优化,获得相对较优初始群体。同时,为维持群体多样性,防止过早收敛,算法以一定概率优化初始群体和染色体的交叉、变异,终止条件为设定最大迭代次数。算法结构采用遗传算法的基本流程[11]。 基于最短完工时间的柔性作业车间分批调度模型及遗传算法已实用于某精密加工车间。文中采用该车间某生产周期内的生产任务作为测试实例。具体描述为:加工4种不同类型的工件,工件产量为8,表4为工序可供选择的设备及加工信息。 表4 工序对应设备及加工信息 算法仿真环境为:Intel(R)Core(TM)2、CPU主频2GHz、内存2GB、Windows XP操作系统,采用C#语言实现。设置遗传算法经验参数:初始种群规模为100,初始染色体优化概率为0.5,交叉概率为 0.5,变异概率为 0.1,算法最大迭代次数为100次。 SPEA作为一类进化算法已被应用于求解FJSLP且取得一定效果[11]。因此,选取 SPEA与文中基于集成思想的IGA分别对上述实例求解并对比。同时,为体现集成化IGA的特点,采用文献[7]提出的一种借助 Witness仿真技术将批量分配与工序调度分开处理的优化方法。建立前文第1节中最短完工时间的数学模型,评价次数设为10000,这里分别给出10次独立运行结果。 分步法首先采用Witness的Optimize功能对工件批量进行优化,获得的工件加工批次及批量如表 5所示;然后,将分割的各批次工件看作独立工件,即将FJSLP转化为FJSP;最后,采用SPEA求解。图4为SPEA求解的最优结果的时间甘特图,图中1.1指工件1的第1道工序,括号内数字为批量。集成化IGA求解时将工件批量与工序调度融合。首先,编码过程包含工件批量与工序调度全部信息;然后,对染色体进行目标优化时设计依据子批优先级平衡设备负荷规则;最后,在解码、交叉变异过程中分别对子批进行工艺排序和工序更新。因此,直接获得各子问题最优解,运行后,获得最优时间甘特图如图5所示。 表5 工件分批结果 表6 算法结果对比 分析表5、表6结果,分步求解方式可分别获得批量优化子问题与工序调度子问题优化解,但难以保证FJSLP整体最优。集成化IGA可对FJSLP整体寻优,算法过程解决了FJSLP的子批与工序同时优的难点。另外,二者运算速度分别为7.23 s和6.58 s,表明IGA过程简单,收敛速度快。 针对柔性分批作业调度问题难以集成求解,文中设计IGA取得较好效果。但该问题在国内外研究仍相对较少,可着重对以下几个方面继续研究:1)考虑划分瓶颈工序与非瓶颈工序,找出影响调度效率的原因并分析;2)同时考虑多资源约束条件下的调度模型;3)研究不确定环境下重调度问题,考虑生产过程中的突发因素影响。 [1] 赵尔恭,饶辉樟. 多品种小批量流水作业生产组织与管理[M].北京:中国铁道出版社,1981. [2] 吴秀丽,李苏剑,杜彦华. 柔性作业车间多品种小批量调度算法研究[J]. 中国机械工程,2010,21(4):424-429. [3] 陶泽,李小军,刘晓霞. 基于Petri网和GA的多目标动态优化调度问题研究[J]. 组合机床与自动化加工技术,2011,(10):5-9. [4] 姚嫣菲. 基于改进遗传算法的车间作业调度问题研究[D].浙江:浙江大学. 2010. [5] Huang R H. Multi-objective job-shop scheduling with lotsplitting production[J]. International Journal of Production Economics,2010,124(1):206-213. [6] 白俊杰,龚毅光,王宁生,等. 批量生产柔性作业车间优化调度研究[J]. 机械科学与技术,2010,29(3):293-298. [7] 曾强,杨育,王小磊,等. 并行机作业车间等量分批多目标优化调度[J]. 计算机集成制造系统,2011,17(4):816-825. [8] 白俊杰,龚毅光,王宁生,等. 多目标柔性作业车间分批优化调度[J]. 计算机集成制造系统,2010,16(2):396-403. [9] 刘明周,张明伟,蒋增强,等. 基于混合粒子群算法的多目标柔性Job-Shop调度方法[J]. 农业机械学报,2008,39(5):122-127. [10] Low C,H Su C M,Huang K I. Benefits of lot splitting in Job Shop scheduling[J]. International Journal of Advanced Manufacturing Technology,2004,24(9-10):773-780. [11] 王凌. 车间调度及其遗传算法[M]. 北京:清华大学出版社,2003. [12] 王云,冯毅雄,谭建荣,等. 柔性作业车间分批调度多目标优化方法[J]. 浙江大学学报(工学版),2011,45(4): 719-726,764.2.3 其他过程设定
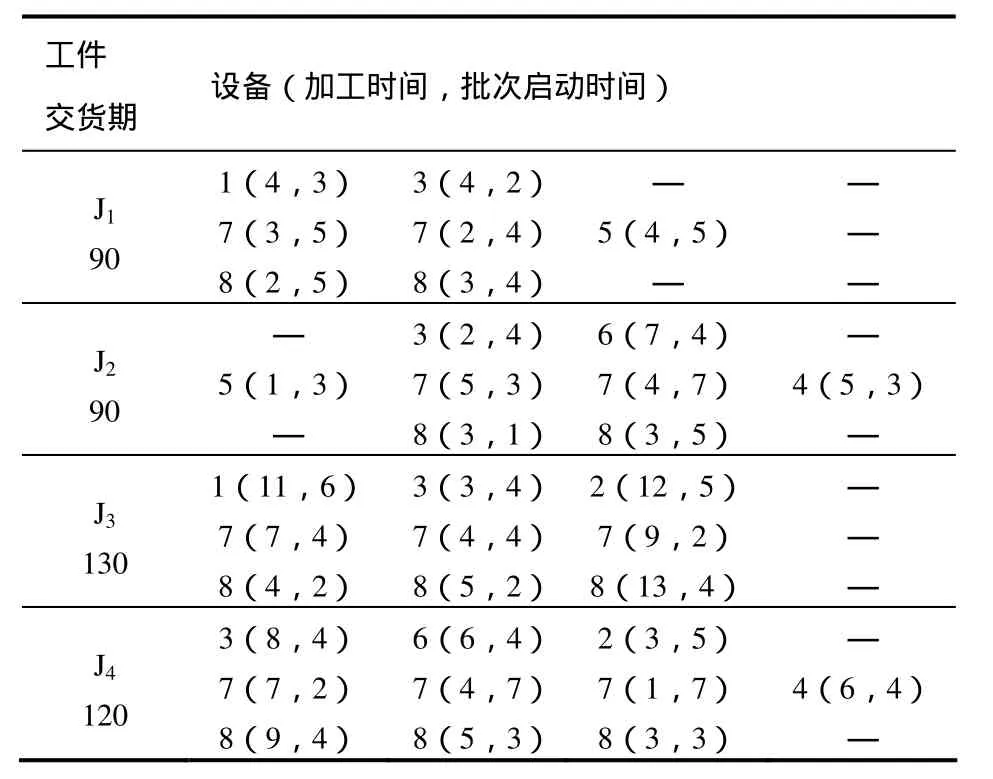
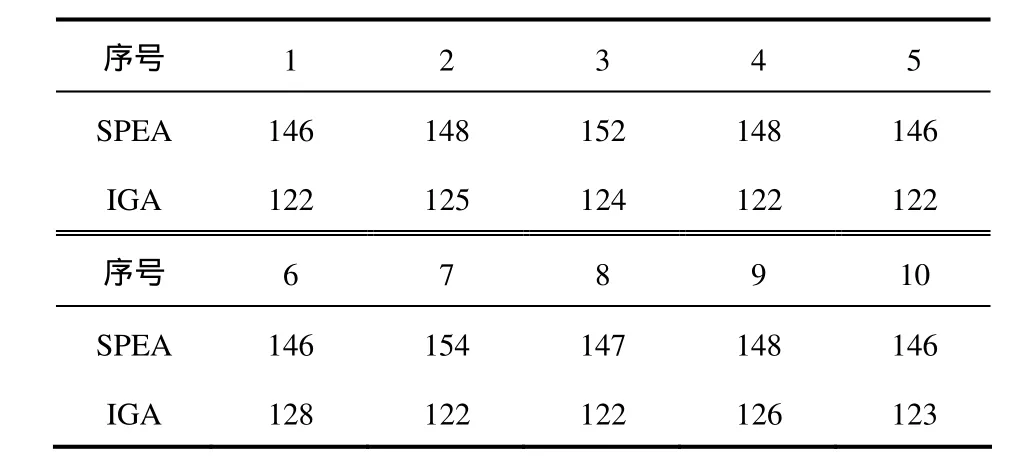
3 实例测试与对比

4 结束语
