一种空间飞网机器人网型保持控制方法
马骏, 黄攀峰, 孟中杰
(1.西北工业大学 航天学院智能机器人研究中心, 陕西 西安 710072; 2.西北工业大学 航天飞行动力学国家重点实验室, 陕西 西安 710072)
一种空间飞网机器人网型保持控制方法
马骏1,2, 黄攀峰1,2, 孟中杰1,2
(1.西北工业大学 航天学院智能机器人研究中心, 陕西 西安 710072; 2.西北工业大学 航天飞行动力学国家重点实验室, 陕西 西安 710072)
针对空间飞网机器人逼近目标过程中的网型保持控制问题,设计了一种基于积分切换函数的滑模变结构控制器,对自主机动单元逼近目标过程中的位置和速度偏差进行控制,保证各自主机动单元以一定的相对速度沿着期望轨迹运动,进而实现网型保持的目的。仿真结果表明,所设计的控制器是合理的,能够达到设计要求。
空间飞网机器人; 自主机动单元; 滑模变结构
0 引言
空间飞网机器人是一种新型的“自主机动单元+柔性网”结构的空间机器人系统,其在空间垃圾清理、失效卫星捕获等空间任务中具有显著的优势。空间飞网机器人的基本思想是多个自主机动单元在空间展开一张具有一定覆盖面积和强度的柔性网,进而多个自主单元牵引柔性网在空间中沿一定的轨道机动飞行,依靠柔性网清扫途经空间范围内的空间垃圾。当柔性网内空间垃圾达到一定数量时,空间飞网机器人在自主单元控制下,将柔性网连同其内部的空间垃圾拖离轨道,或者降低轨道坠入大气层销毁,或者将空间垃圾拖入坟墓轨道。空间飞网机器人在逼近目标的过程中,由于自主机动单元速度、方向的改变,会使柔性网的网型发生变化,无法保持展开状态,同时柔性网也会使自主机动单元偏离期望逼近轨迹。因此,必须对空间飞网机器人逼近目标过程中的网型保持问题展开研究。
本文首先采用质量集中法建立了空间飞网机器人逼近过程的动力学模型,针对逼近目标过程中的网型保持控制问题,设计了一种基于积分切换函数的滑模变结构控制器,实现对自主机动单元的位置和速度偏差的控制,进而达到网型保持的目的,并通过数字仿真进行了验证和分析,最后给出了研究结论。
1 空间飞网机器人动力学模型
空间飞网机器人的典型结构如图1所示。柔性网结构使空间飞网机器人在空间中的动力学结构变得非常复杂,很难建立其精确的动力学模型。
国内外关于柔性网结构动力学建模的研究对空间飞网机器人的动力学建模方法具有一定的参考价值。文献[1-5]中将柔性网离散化为质点和弹性杆单元的结构,在此基础上建立了柔性网的动力学模型;文献[6]中采用质子弹簧模型建立了网结构的动力学模型。因此质量集中方法是目前应用较为广泛的柔性网动力学建模方法,能够在一定程度上反映柔性网在空间中的动力学特性。本文采用质量集中法建立空间飞网机器人的动力学模型。建模之前首先做出以下简化假设:
(1)忽略柔性网材料阻尼的影响,将自主机动单元看作质量点,忽略其姿态变化对空间飞网机器人运动的影响;
(2)自主机动单元在参考系三个方向的正反均安装了推力控制执行机构;
(3)空间飞网机器人与目标运行在同一圆轨道。
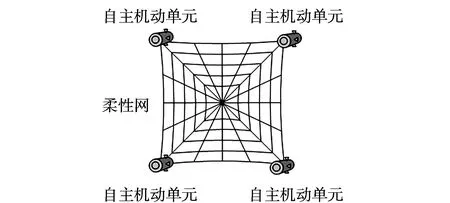
图1 空间飞网机器人Fig.1 Maneuvering-net space robot
以目标(待清理空间垃圾)为原点建立轨道坐标系Otxyz,如图2所示。其中x轴沿目标运行方向,y轴垂直于轨道平面,与轨道角速度方向一致,z轴沿目标径向方向。轨道坐标系Otxyz即为建模参考坐标系。
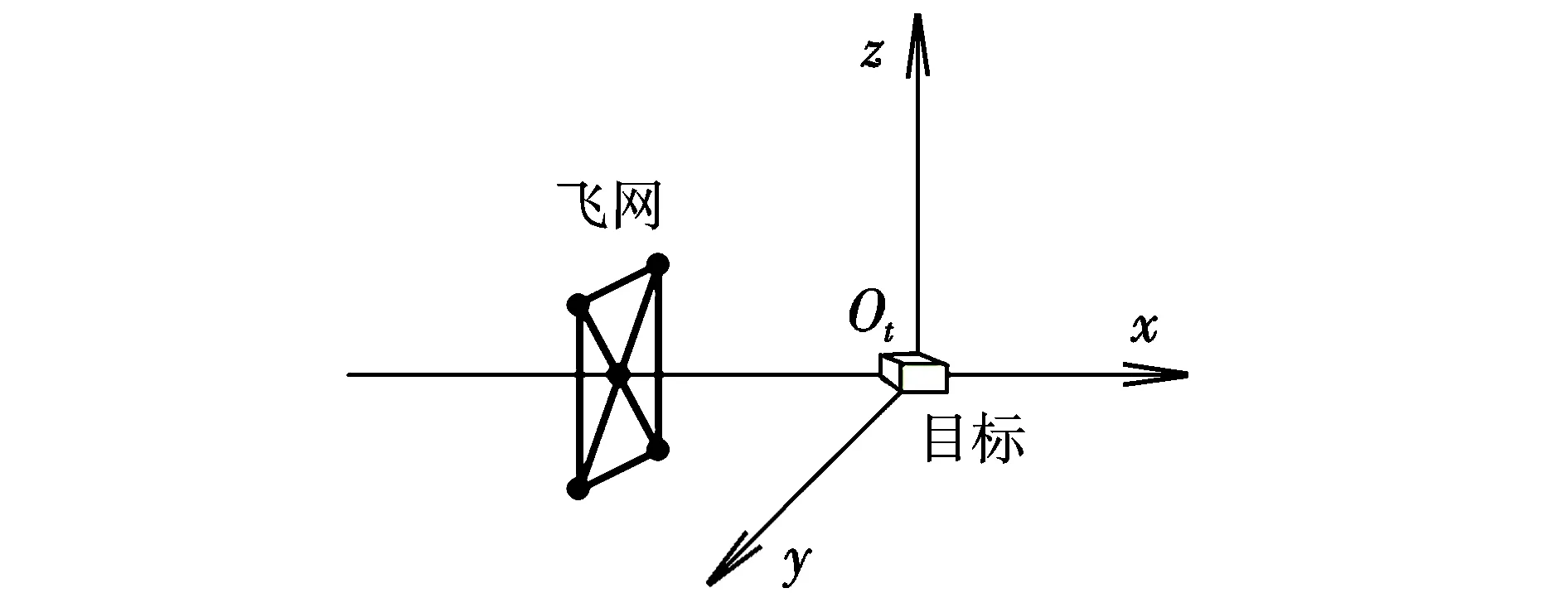
图2 参考坐标系Fig.2 Reference frame
如图3所示,将柔性网离散化为m×n个质点(i,j)的集合,各质点与相邻的质点之间依靠只承受拉力不承受压力的无质量弹性杆连接,并且弹性杆的弹性力仅由弹性杆拉伸应变决定。代表自主机动单元的质点分别位于柔性网离散化模型的4个角对角位置,即质点(1,1),(1,n),(m,1)和(m,n)。将质点(i,j)的质量表示为mi,j,质点(i,j)在参考轨道坐标系下的位置矢量为:
Ri,j=[xi,j,yi,j,zi,j]T
(1)
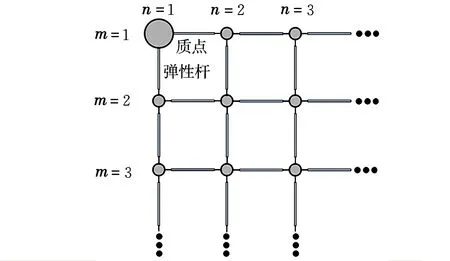
图3 质点-弹性杆模型Fig.3 Mass-spring truss model
由于空间飞网机器人的任务距离为几十米到几公里范围内,与卫星等航天器相比,任务过程很短,地球形状摄动和大气阻力摄动的影响很小,因此在动力学模型的仿真与分析中忽略摄动力的影响,则质点(i,j)在轨道坐标系下受到的外力可表示为:
Fi,j=[Fx;i,j,Fy;i,j,Fz;i,j]T=fi,j+Ti,j
(2)
式中,fi,j为质点(i,j)的自主控制力,仅存在于代表自主机动单元的质点上;Ti,j为质点(i,j)受到相邻质点的弹性力矢量和,与质点连接的弹性杆应变有关。
各质点受到与之连接的弹性杆弹性力的作用,位于对角的质点受到两个方向的弹性力作用,位于柔性网边上的质点受到3个方向的弹性力作用,其它质点则受到4个方向的弹性力作用。设d为连接两质点的弹性杆的标称长度,则相邻质点间弹性力T′的幅值可表示为:
(3)
式中,ls为弹性杆的实际长度;d为弹性杆的标称长度;E为弹性杆弹性模量;A为弹性杆截面积。当ls≤d时,弹性力为0,弹性杆处于松弛状态。以受到4个方向弹性力的质点(i,j)为例,其受到4个方向的弹性力矢量和为:
(4)
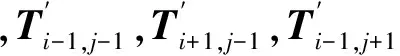
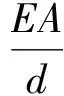
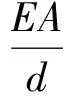
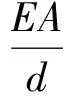
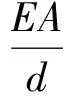
(5)
设参考系的单位坐标列阵为:
e=[ex,ey,ez]T
(6)
式中,ex,ey和ez分别为参考系3个坐标轴的单位坐标向量。两个质点间受到的弹性力Ti,j在3个坐标系上的分量可表示为:
Ti,,j=Tx;i,,jex+Ty;i,,jey+Tz;i,,jez
(7)
在建立的参考轨道坐标系下的Hill方程[7]为:
(8)
式中,ω为轨道平均角速度;ax,ay,az为追踪航天器的加速度。将式(2)代入式(8)得:
(9)
式(9)即为空间飞网机器人在参考轨道坐标系下的动力学模型。将柔性网对自主机动单元的弹性力作用看作干扰,则自主机动单元的动力学模型为:
(10)
式中,(i,j)=(1,1),(1,n),(m,1),(m,n),取:
(11)
(12)
则式(10)可写为:
(13)
其中:
(14)
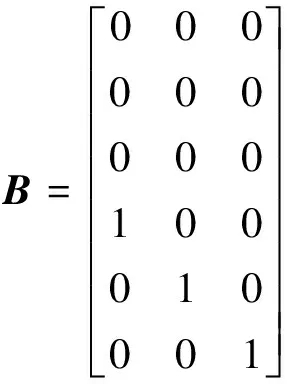
(15)
理想的空间飞网机器人在逼近目标的过程中,各自主机动单元以一定的逼近速度沿期望的轨迹运动是柔性网网型能够保持的必要条件。各自主机动单元偏离理想轨迹以及逼近速度的偏差会导致柔性网网型无法保持展开状态,柔性网弹性力的作用也会使自主机动单元进一步偏离期望轨迹。因此,将柔性网弹性力看作干扰时,网型保持控制即自主机动单元在自身控制力作用下消除实际轨迹与期望轨迹的偏差,进而实现柔性网网型保持。本文在建立的动力学模型基础上,设计一种基于积分切换函数的滑模控制器[7],实现自主机动单元对期望轨迹和逼近速度的跟踪控制。
2 滑模变结构控制器设计
设计积分型切换函数[8]为:
(16)
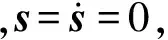
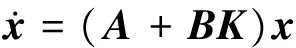
(17)
通过设计状态反馈增益矩阵K可以实现对期望xref的跟踪控制。滑模控制器设计为:
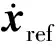
(18)
式中,xe=xref-x;K<0;f≥|δ|,δ为跟踪误差;积分切换函数s为:
(19)
稳定性分析:
=CB[E-fsgn(s)]
(20)
则有:
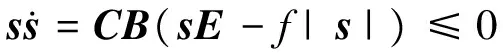
(21)
因此控制系统的滑模到达条件得到满足, 系统能够进入滑模状态。
3 数字仿真与结果分析
主要仿真参数如下:目标轨道高度为700 km,自主机动单元质量为10 kg,柔性网质点质量为0.1 kg,E=4 Gpa,d=0.5 m,A=3.14 mm2,m×n为11×11。假设空间飞网机器人向目标逼近过程为V-bar逼近,逼近开始时空间飞网机器人已完全展开,空间飞网机器人与目标相距500 m,并且柔性网网面与逼近方向垂直,各自主机动单元与柔性网具有相同的逼近速度。理想状态下,空间飞网机器人以3 m/s的速度向目标逼近,即所有自主机动单元与柔性网在x方向具有3 m/s的逼近速度,在y和z方向速度为0。若单个自主机动单元(以自主机动单元1为例)逼近开始后在x方向的逼近速度为2 m/s,在y和z方向均产生0.1 m/s的速度偏差,此时空间飞网机器人的网型变化如图4所示。从图中可以看到,柔性网的网型不再保持展开状态,自主机动单元1也偏离了期望轨迹。自主机动单元1逼近速度与理想逼近速度的偏差将导致柔性网网型无法保持理想的展开状态。
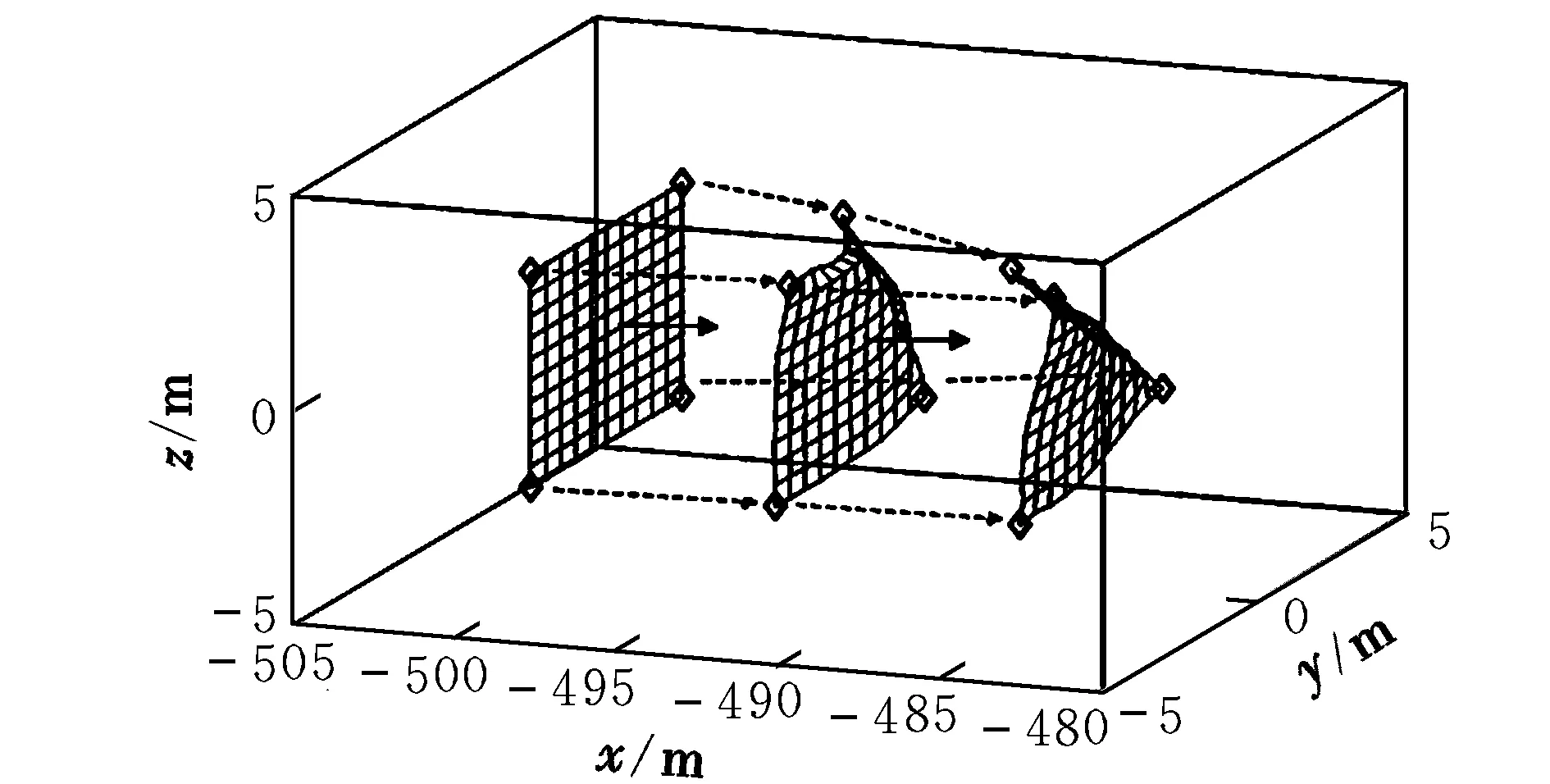
图4 速度偏差引起的网型变化Fig.4 Variation of shape caused by velocity error
下面采用基于积分切换函数的滑模控制器实现自主机动单元对期望轨迹和逼近速度的跟踪控制。同样以自主机动单元1为例,假设初始状态时其在x方向的逼近速度为2 m/s,在y和z方向均产生0.1 m/s的速度偏差,x方向期望逼近速度为3 m/s,y和z方向期望逼近速度均为0,滑模控制器参数取为:
f=1


图5和图6分别为自主机动单元1在滑模控制器作用下位置和逼近速度随时间的变化。从图中可以看到,自主机动单元1的位置偏差和速度误差能够很快得到控制,在x方向的逼近速度逐渐稳定在3 m/s,在y和z方向的逼近速度逐渐稳定在0。
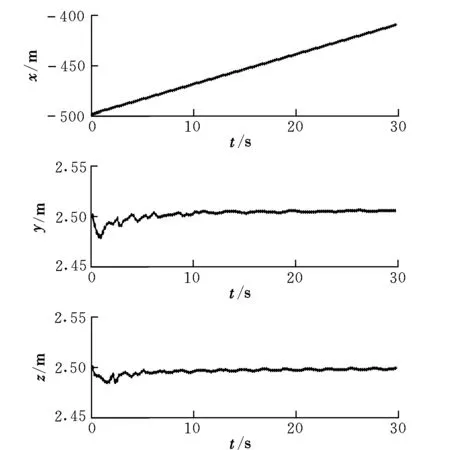
图5 位置变化Fig.5 Variation of the position
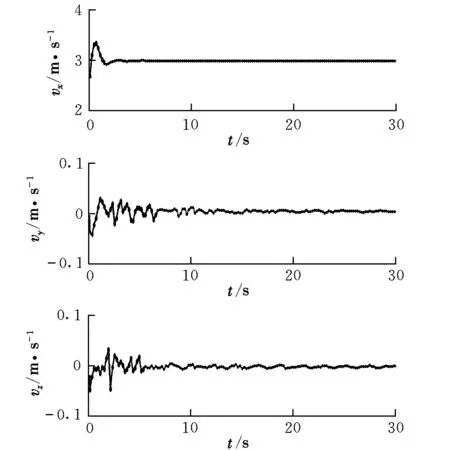
图6 逼近速度变化Fig.6 Variation of the approaching velocity
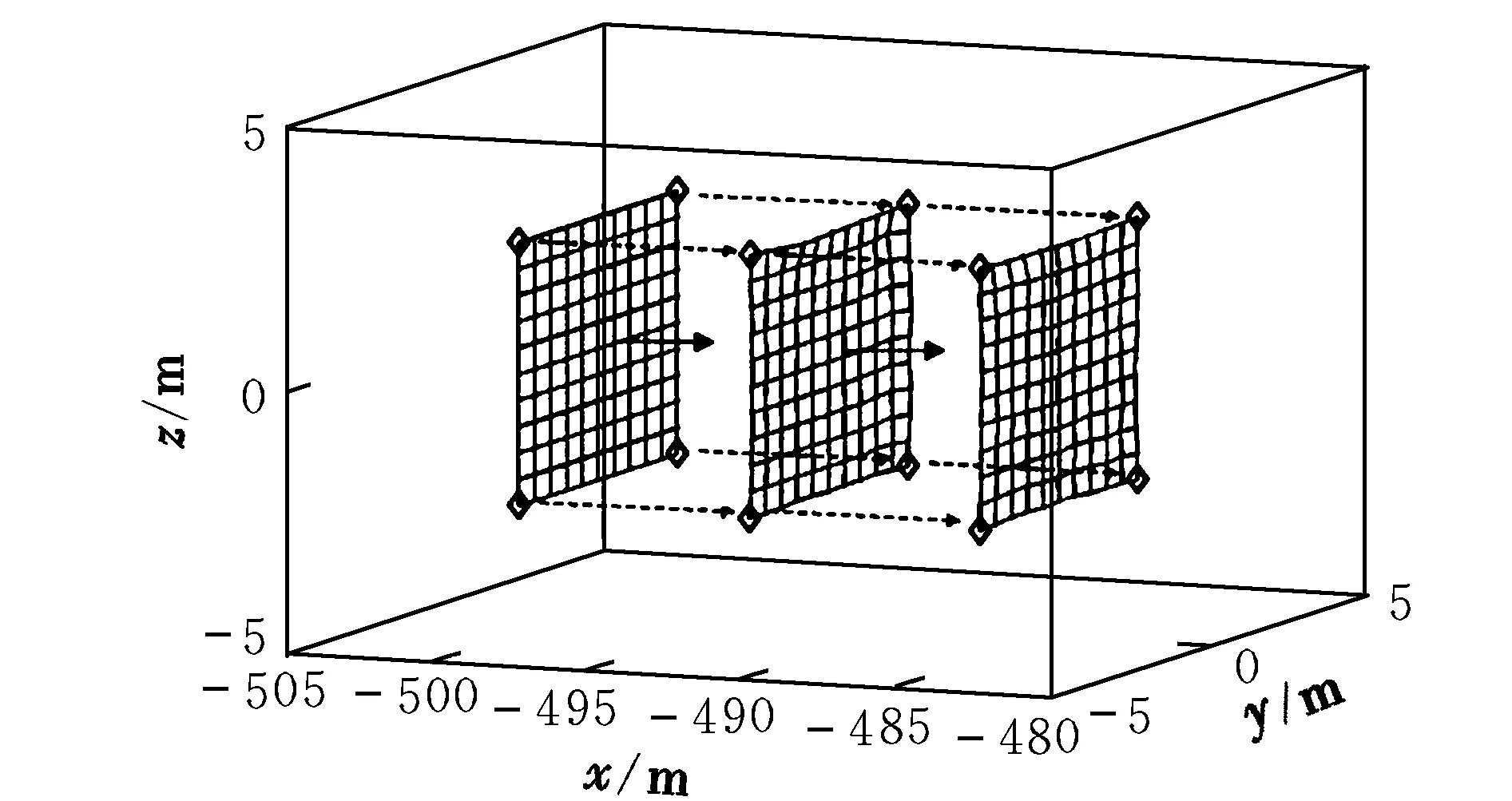
图7 控制器作用下的网型变化Fig.7 Variation of shape in the control mode
图7为滑模控制器作用下的网型变化。与图4中的网型变化相比,柔性网的网型基本保持在展开状态向目标逼近。由此可见,在设计的控制器作用下,自主机动单元能够有效地对期望轨迹和逼近速度进行跟踪控制,进而实现逼近目标过程中的柔性网网型保持的目的。
4 结束语
介绍了一种新型的空间飞网机器人系统,设计了一种基于积分切换函数的滑模变结构控制器,对空间飞网机器人的自主机动单元逼近目标过程中的位置和速度偏差进行控制,进而实现网型保持的目的。仿真结果表明:所提出的网型保持控制方法能够有效地实现空间飞网机器人逼近目标过程中的网型保持控制的目的。
[1] 于洋,宝音贺西,李俊峰.空间飞网抛射展开过程动力学建模与仿真[J].宇航学报,2010,31(5):1289-1296.
[2] 李京阳,于洋,宝音贺西,等.空间飞网两种动力学模型的比较[J].力学学报,2011,43(3):542-550.
[3] 敬忠良,袁建平,李恒年,等. 航天器自主操作的测量与控制[M].北京:中国宇航出版社,2011:493-518.
[4] 陈钦.空间绳网系统设计与动力学研究[D].长沙:国防科学技术大学,2010.
[5] Mattias Gärdsback,Gunnar Tibert.Deployment control of spinning space webs[J].Journal of guidance,control,and dynamics,2009,32(1):40-50.
[6] Provot X.Deformation constraints in a mass-spring model to describe rigid cloth behavior [C]//Proceedings of graphics interface.Quebec,Canada,1995:147-154.
[7] 朱仁璋.航天器交会对接技术[M].北京:国防工业出版社,2007:23-31.
[8] 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005:427-43.
(编辑:姚妙慧)
Amaintainingcontrolmethodformaneuvering-netspacerobot
MA Jun1, 2, HUANG Pan-feng1, 2, MENG Zhong-jie1, 2
(1.Research Center of Intelligent Robotics, College of Astronautics, NWPU, Xi’an 710072, China; 2.National Key Laboratory of Aerospace Flight Dynamics, NWPU, Xi’an 710072, China)
In order to maintain the shape of space net in approaching phase, an integral-switch sliding-mode variable structure controller was introduced to control the error of position and velocity of the autonomous maneuvering units. The simulation results show that the sliding-mode variable structure controller is effective and feasible on the maintenance control for the shape of the space net.
maneuvering-net space robot; autonomous maneuvering unit; sliding-mode variable structure
V476.5
A
1002-0853(2013)06-0561-05
2013-03-22;
2013-06-16; < class="emphasis_bold">网络出版时间
时间:2013-10-22 14:16
国家自然科学基金资助(11272256;61005062)
马骏(1985-),男,陕西商洛人,博士研究生,研究方向为空间机器人技术。

