无人机自主着陆的双环混合迭代滑模控制
高杨军, 孙秀霞, 刘宇坤, 刘希
(空军工程大学 航空航天工程学院, 陕西 西安 710038)
无人机自主着陆的双环混合迭代滑模控制
高杨军, 孙秀霞, 刘宇坤, 刘希
(空军工程大学 航空航天工程学院, 陕西 西安 710038)
提出了一种无人机自主着陆精确轨迹跟踪的双环混合迭代滑模控制器。外环和内环均采用两级混合迭代滑模控制方法,第一级滑模采用全局动态切换函数,第二级迭代滑模切换函数中引入了非线性积分项,并采用准滑模控制的策略。该方法消除了滑模控制的到达运动阶段,在保持传统积分滑模控制精度的同时,还消除了积分滑模固有的超调和变结构控制的抖振问题。通过在外环滑模切换函数中引入俯仰角的微分项,直接设计俯仰角微分指令,克服了传统方法需要求俯仰角指令微分的缺点。理论推导和仿真结果均表明,该方法具有良好的动态跟踪性能和很强的鲁棒性。
双环控制; 全局滑模; 积分滑模; 高阶滑模; 迭代滑模
0 引言
无人机凭借其机动灵活、成本低、无人驾驶、能自主执行任务等诸多优势,已成为全球研究和发展的热点。自主着陆是无人机安全回收的前提,是无人机的关键技术之一[1]。在飞行着陆期间,需要在大气紊流、阵风、风切变等干扰环境中对飞行轨迹进行精确跟踪控制。同时,飞机是一个复杂的非线性控制对象,不可能获得精确的数学模型。因此,自主着陆控制是一个典型的鲁棒控制问题,这本身就是控制领域一个具有挑战性的课题,吸引着众多的专家和学者进行研究。
文献[2]设计了一种经典PID控制器加预测控制器的分层控制系统;文献[3]根据无人机精确进场自动着陆性能要求,利用线性矩阵不等式凸优化方法设计鲁棒H∞控制器;文献[1,4]针对纵向着陆的线性方程采用稳定逆控制方法并结合反馈控制器设计了自动着陆控制律。以上控制器都是基于线性小扰动方程设计的。由于实际模型的非线性,在实际工程应用中都是采用增益调度的方法。文献[5]采用非线性动态逆控制方法来解决无人机自动着陆阶段的非线性控制问题。文献[6]利用自抗扰技术设计了自动着陆控制系统,能够实时估计和补偿动态干扰,但自抗扰控制器中的扩张状态观测器对量测噪声非常脆弱。文献[7]利用增长型神经网络设计了一种自适应反推的控制方法,然而神经网络的学习参数难以设定,其工程应用还存在问题。滑模控制由于算法简单、 响应严重制约着滑模控制的工程应用,Slotine等[8]引入了“准滑模控制”和“边界层”的概念,采用饱和函数代替切换函数,有效地避免或削弱了抖振,为变结构控制的工程应用开辟了道路。但是,饱和函数的引入会导致一定的稳态误差。为了消除稳态误差,T L Chern等[9-11]在滑模面的设计中引入了积分项,提出了一种积分变结构控制方案。积分滑模的精确控制使得滑模控制开始应用于飞行控制系统中[12]。但是积分滑模控制的阶跃响应存在超调,暂态性能较差,难以应用于固定翼无人机的自主着陆精确轨迹跟踪控制中。
迄今为止,暂未见到单纯滑模控制应用于固定翼飞机自主着陆轨迹跟踪控制的相关文献。基于此,本文提出了一种双环混合迭代滑模的控制方法,融合了全局滑模、准滑模和积分滑模的优点,克服了准滑模控制存在稳态跟踪误差、积分滑模控制存在超调和滑模变结构控制存在抖振的问题,具有精确的动态跟踪性能和很强的鲁棒性。通过在外环滑模切换函数中引入俯仰角的微分项,直接设计俯仰角微分指令,克服了传统双环控制方法需要求俯仰角指令微分的缺点。
1 无人机纵向非线性模型
无人机是具有六自由度的复杂非线性系统,对于飞机的纯纵向运动,可以假设φ=ψ=β=p=r=0,采用文献[7]建立的纵向非线性运动方程:
(1)
其中:
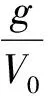
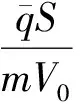
式中,γ为航迹角;θ为俯仰角;δe为升降舵偏角;dw(γ,θ),dn(γ,θ,q,δe)为模型参数摄动和外界大气干扰的总和。
假设1:dw(γ,θ),dn(γ,θ,q,δe)为不确定有界函数,满足:
(2)
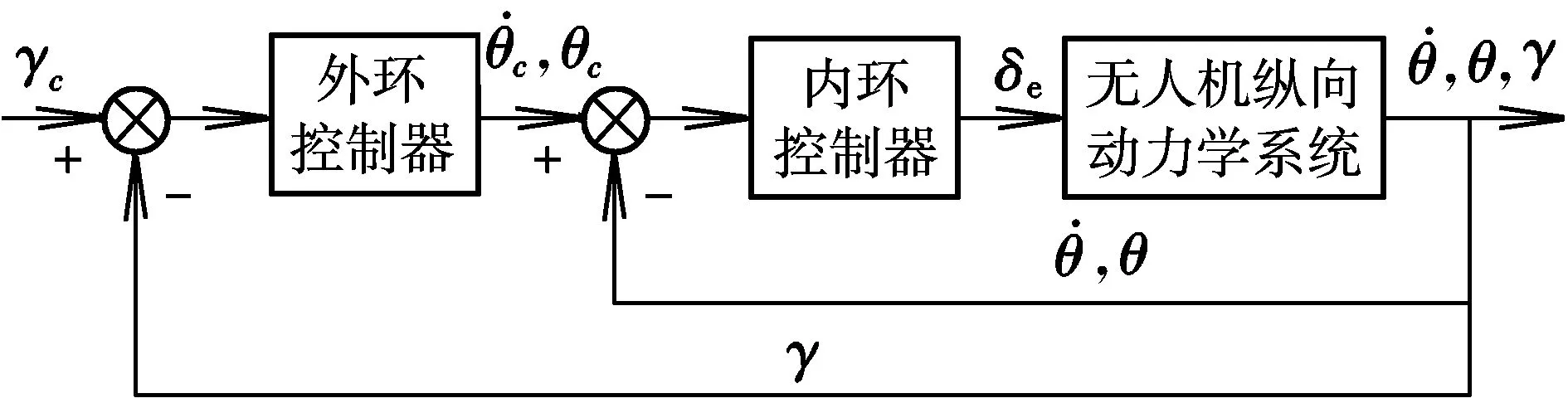
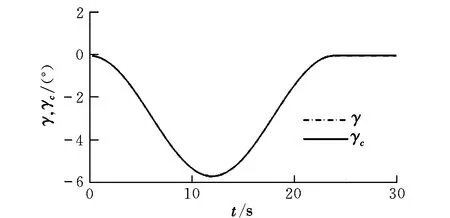
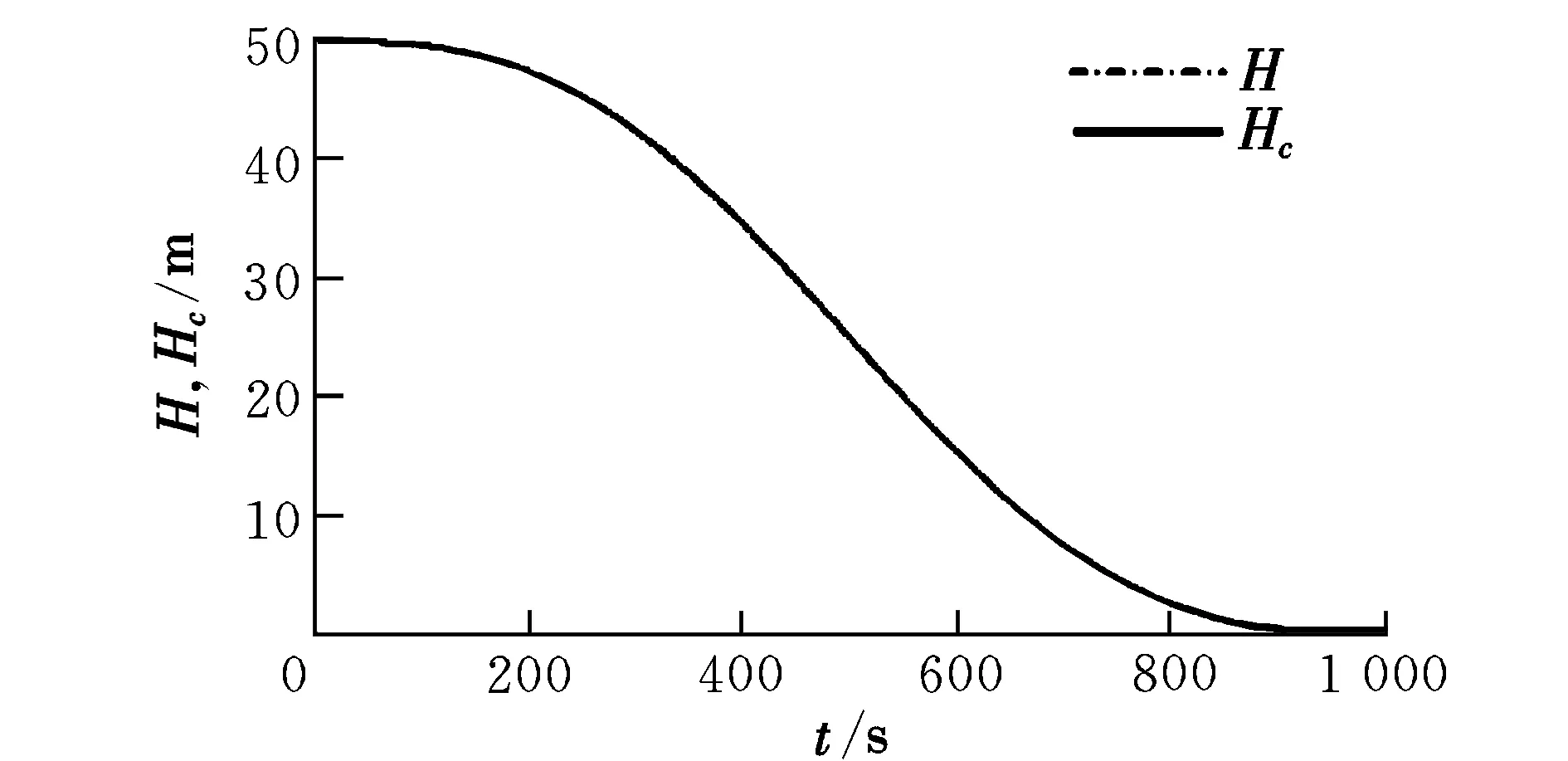
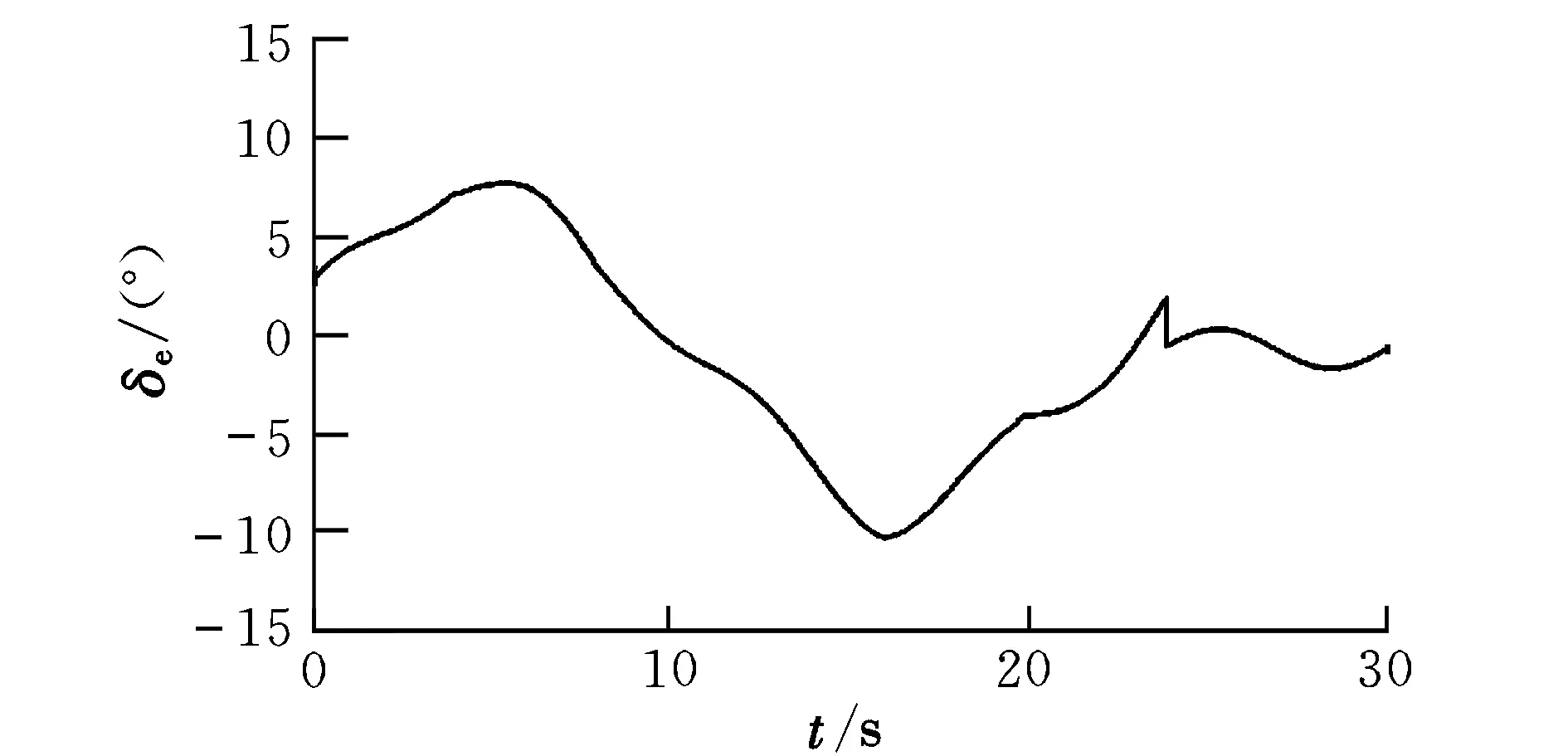
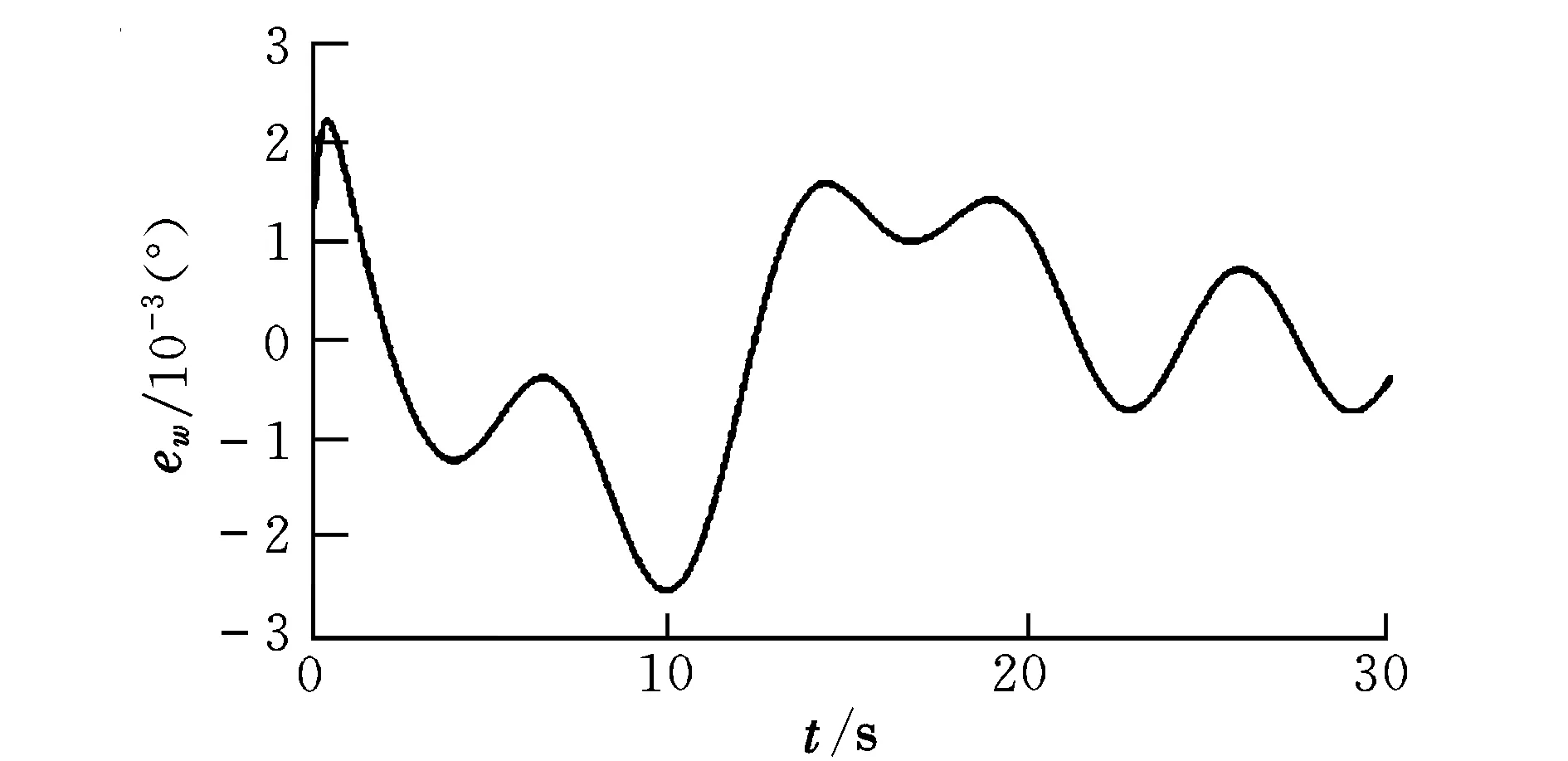
dn(γ,θ,q,δe) (3) 控制的目标是通过输入δe使输出γ跟踪期望的航迹角。 图1 双环控制系统结构Fig.1 Structure of double-loop control system 2.1 外环混合迭代滑模控制律设计 外环滑模主要实现参考轨迹角指令的跟踪,为内环提供参考俯仰角及其微分指令。定义误差及其混合迭代切换函数分别为: (4) 式中,aw>0,bw>0,cw>0为待设计参数;fw(t)是为了达到全局滑模而设计的参考趋近函数,具有一阶导数,且满足: (5) 通常可将fw(t)设计为: f(t)=fw(0)exp(-kwt) (6) 式中,kw为一个正的常数。式(4)中的gw(·)为一类“小变量大增益,大变量小增益”的非线性函数,且对于任意x,满足: (7) 本文gw(·)取双曲正切函数tanh(·)。 定理1:对于无人机纵向系统式(1),设计混合迭代切换函数式(4),设计如式(8)所示的俯仰角微分指令: (8) (1)若系统受到的干扰为常值或最终为常值,则当t→∞时,稳态跟踪误差ew→0。 (2)若系统受到的干扰为动态干扰,则当t→∞时,跟踪误差ew满足: ew≤2(μw/cw) (9) (10) ≤-ηws2w 又s2w(0)=0<μw,所以s2w可以稳定在边界层内,即下式成立: s2w<μw (11) (1)若系统受到的干扰为常值或最终为常值,则有: (12) 记σ=(Dw(γ,θ)+ηw)/μw,由式(4)、式(8)知,滑模切换函数s2w在边界层内s2w≤μ的运动轨迹可以描述为: (13) (14) (15) 于是,有: (16) (17) 若Iw>μw/aw,则由式(7)、式(11)和式(17)可得: (18) 又t=0时,Iw=0,所以 Iw≤μw/aw (19) 由式(4)、式(11)、式(19)可得: s1w=s2w-awIw ≤s2w+awIw≤2μw (20) 对式(4)进行Laplace变换可得: ew(p)=[1/(p+cw)][s1w(p)+fw(p)] (21) 式中,p为Laplace算子。 令: H(p)=1/(p+cw) (22) 显然,H(p)是输入有界、输出稳定的。其脉冲响应为: h(t)=e-cwt (23) 因为要求的是稳态误差,所以可以忽略初始状态的影响。对任意输入s1w,H(p)的零状态响应为: (24) 上式两边取极限,由式(5)、式(20)得: (25) 证毕。 2.2 内环混合迭代滑模控制律设计 内环滑模通过设计升降舵偏角,跟踪外环提供的参考俯仰角及其微分指令。定义误差及其混合迭代切换函数分别为: (26) 式中,函数fn(t),gn(·)与fw(t),gw(·)具有相同的性质和形式。 定理2:对于无人机纵向系统式(1),设计混合迭代切换函数式(26),设计式(27)所示的舵偏角指令: (27) 式中,gn(·)=tanh(·)。 (1)若系统受到的干扰为常值或最终为常值,则当t→∞时,稳态跟踪误差en→0。 (2)若系统受到的干扰为动态干扰,则当t→∞时,跟踪误差en满足: |en|≤2(μn/cn) (28) 定理2的证明与定理1的思路相同,略。 0.75q+0.6 sint =Dw(γ,θ) dn(γ,θ,q,δe) =0.2+25q-13.3θ-13.3γ- 2.3δe+2.8 sint <5.2+25q+14θ+14γ+3δe+3 =Dn(γ,θ,q,δe) 取控制参数为:cw1=1,aw=0.1,bw=1,μw=0.2;cn=3,an=0.3,bn=1,μw=0.1。设飞机在H0=50 m的空中平飞,需要飞行水平距离xd-x0=1 000 m后着陆。在着陆过程中,保持速度V0不变,初始状态γ0=0,θ0=6°,q0=0。设飞行航迹角指令为: (29) 式中,x为飞行水平距离。 设x0=0,对系统进行仿真,结果如图2~图5所示。由仿真结果可以看出,飞行着陆轨迹很好地跟踪了期望轨迹,基本没有抖振和超调现象。由图5可以看出,eγ<4×10-3<2(μw/cw),满足定理1。 图2 航迹角曲线Fig.2 Correlation curve of flight path angle trajectory 图3 着陆轨迹曲线Fig.3 Longitudinal auto-landing trajectory 图4 升降舵偏角δe曲线Fig.4 Time response of elevator deflection 图5 航迹角跟踪误差ew曲线Fig.5 Tracking error ew of flight path angle 本文针对无人机自主着陆的精确轨迹跟踪问题,提出了一种双环混合迭代滑模的控制策略。该方法融合了全局滑模、积分滑模和准滑模控制的优点,克服了传统双环控制需要求解俯仰角指令微分的缺点和积分滑模固有的超调现象,消除了稳态跟踪误差和变结构控制方法存在的抖振。理论推导和仿真结果均表明,该方法具有很强的鲁棒性和良好的动态跟踪性能。此外,该方法的鲁棒切换项可以作为神经网络的学习导师,结合神经网络的非线性逼近能力,减少建模误差对跟踪性能的影响。 [1] 张建宏,张平.无人机自主精确着陆控制律设计及仿真研究[J].系统仿真学报,2009,21(3):743-748. [2] 吴成富,冯乐.模型预测控制算法在飞机自动着陆控制系统中的应用[J].西北工业大学学报,2004,22(2):140-143. [3] 郭艳艳,陈澜.无人机着陆抗风鲁棒H∞控制器设计研究[J].计算机测量与控制,2010,18(2):348-350. [4] 车军,张新国.自动着陆精确轨迹跟踪控制[J].北京航空航天大学学报,2005,31(9):975-979. [5] 韩英华,范彦铭.基于非线性动态逆的无人机自动着陆控制系统[J].航空学报,2008,29 (S1):66-71. [6] Xiong Hua,Yi Jian-qiang.Anti-crosswind autolanding of UAVs based on active disturbance rejection control[C]//AIAA Guidance,Navigation, and Control Conference.Canada:Toronto,Ontario,2010:7734-7747. [7] Yi Luo,Yoo Hsiu Yeh.Adaptive backstepping design for a longitudinal UAV model utilizing a fully tuned growing radial basis function network [C]//Infotech@Aerospace Conference and Exhibit. Red Hook,N Y:Curran Associates,2011:1451-1473. [8] Slotine J J,Sastry S S.Tracking control of nonlinear systems using sliding surfaces with application to robot manipulator[J].International Journal of Control,1983,38(2):465-492. [9] Chern T L,Wu Y C.Design of integral variable structure controller and application to electrohydraulic velocity servosystems[J].IEE Proceedings-D,1991,138(5):439-444. [10] Chern T L,Wu Y C.Integral variable structure control approach for robot manipulators[J].IEE Proceedings-D,1992,139(2):161-166. [11] Chern T L,Wong J S.DSP based integral variable structure control for motor servo drives[J].Control Theory and Applications,1995,142(5):444-450. [12] Huang Y J,Kuo T C,Way H K.Robust vertical takeoff and landing aircraft control via integral sliding mode[J].Control Theory and Applications,2003,150(4):383-388. [13] Giampiero Campa.Design and flight-testing of non-linear formation control laws [J].Control Engineering Practice,2007,15 (3):1077-1092. Double-loophybriditerativequasi-slidingmodecontrolstrategyforautolandingofUAV GAO Yang-jun, SUN Xiu-xia, LIU Yu-kun, LIU Xi (Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China) A novel double-loop hybrid iterative quasi-sliding mode control strategy was presented for autolanding of UAV. Both out loop and inner loop use two-rank hybrid iterative quasi-sliding mode control, of which the first rank uses global dynamic sliding-mode switch function and the second rank uses switch function with nonlinear integrator and quasi-sliding mode control strategy. While maintaining the tracking accuracy of the traditional integral sliding mode control, the strategy eliminates the reaching stage of sliding mode controller, avoids overshoot of integral sliding mode control and inherent chattering of sliding mode variable structure controller. And it overcomes the deficiency of conventional double-loop control which has to make differential of pitch angle signal. Both theory and simulation results showed the excellent dynamic tracking and strong robust capability of the proposed strategy. double-loop control; global sliding mode; integral sliding mode; higher-order sliding mode; iterative sliding mode V249.1; V279 A 1002-0853(2013)06-0521-05 2013-04-08; 2013-09-04; < class="emphasis_bold">网络出版时间 时间:2013-10-22 14:13 航空科学基金资助(20121396008) 高杨军(1988-),男,湖北武汉人,硕士研究生,研究方向为控制理论与控制工程。 (编辑:姚妙慧)2 双环混合迭代滑模控制器设计
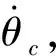
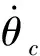
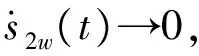

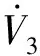
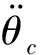
3 仿真算例
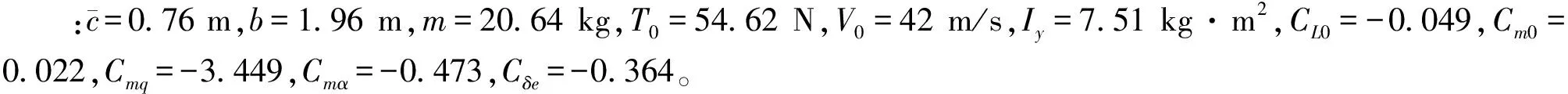
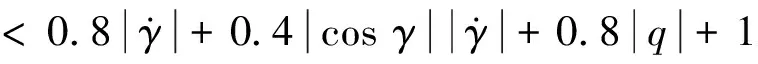
4 结束语

