基于系统动力学的流域农村面源污染生态补偿

曾 霞，侯 兵

(1.中南财经政法大学，湖北 武汉 430073;2.湖北经济学院，湖北 武汉 430205;3.华北水利水电大学，河南 郑州 450045)

一般而言，流域所在地的政府是主要的水资源管理者，这种依赖公共资源来维持健康的水生态环境使得政府的财政压力巨大，而且，由于没有其他相关利益集团参与，效率和可持续性较差.从长远来看，多元化的生态补偿是流域水资源管理的必然选择，是保护流域生态环境，实现流域经济可持续发展的重要途径［1－4］.

流域生态补偿问题涉及资源环境与社会经济，三者相互影响、相互依存.如何研究这个系统之间错综复杂的关系，系统动力学是较为理想的工具.系统动力学依靠系统理论分析系统的结构和层次，依靠自动控制论的反馈原理对系统进行调节，依靠信息论中信息传递原理来描述系统工作原理，并采用电子计算机对系统动态行为进行模拟，其本质是带时滞的一阶微分方程组，适合分析和研究动态复杂的社会经济系统，是研究水资源系统的重要方法之一［5－8］.

系统动力学在水资源承载力、需水量预测、水资源供需平衡分析等方面应用广泛［9－12］.这里从流域多元生态补偿的角度出发，尝试用系统动力学方法建立流域农村面源污染的生态补偿模型，并以化肥污染为例进行了实证分析，由此针对流域农村面源污染问题提出了生态补偿的方案，为决策制定者提供参考.

1 流域农村面源污染的生态补偿模型

1.1 系统因果关系分析

长期措施与短期措施并重是治理流域农村面源污染的有效方式，设立生态基金是首要的措施，将生态基金用于治理污染的长期措施与短期措施.对于流域的农村而言，长期措施一般主要包括生态养殖、生态农业、生态渔业、生态湿地建设以及农村自来水改造;短期措施一般主要包括垃圾回收、对民众的宣传教育以及垃圾集中处理.虽然在实施生态养殖、生态农业、生态渔业、生态旅游过程中也会产生污染，但包括生态养殖、生态农业、生态渔业、生态湿地在内的长期措施与作为短期措施的垃圾回收可以产生经济效益，并且政府由此得到的税收与国家项目补偿资金和民间资本等其他资金，可以再投入到生态基金，形成污染治理与经济发展的良性循环，从而实现资源利用与经济效益的可持续发展.于是，利用Vensim 软件绘制流域农村面源污染的生态补偿模型的系统因果关系如图1 所示.

通过因果关系图可以看出，流域农村面源污染的生态补偿不仅仅是单一化的政府补偿，其生态补偿基金的来源除了国家项目资金，还有生态基金投入的生态养殖、生态农业、生态渔业、生态旅游和垃圾回收带来的收益，以及民间资本等其他资金.这种多元化的补偿方式使生态补偿由“输血型”补偿变为“造血型”补偿，使流域农村面源污染的治理和社会经济得到可持续的发展.

图1 农村面源污染的生态补偿系统因果关系图

1.2 系统流图绘制与系统方程式

根据收集到的数据，考虑生态农业方式下，运用系统动力学的方法分析污染治理量与资金补偿量的变化趋势及交互影响.为了简化模型，不妨只考虑化肥造成的污染，其他污染源情形可类似处理，污染的治理方式为减少化肥使用量.

基于上述分析，可构建污染治理总量、补偿资金总量以及相关变量之间的系统流图，如图2 所示.

图2 污染治理总量与补偿资金总量系统流图

图2 中，污染治理总量与资金补偿总量是水平变量，其对应的水平方程为:

式中:PTK为K 时刻污染治理总量;PTJ为J 时刻的污染治理总量;PV 为污染治理总量;KTK为K 时刻的资金补偿总量;KTJ为J 时刻的资金补偿总量.

图2 中，没有箭头指入的变量均为辅助变量，包括最大污染治理量(化肥使用量)、初始污染治理量、化肥单价、治理污染固定费用、普通水稻单价、普通水稻产量、有机水稻单价以及有机水稻产量，需赋予辅助变量常数值.模型的实证分析中，辅助变量的初始值来源于实地考察调研.相应的辅助方程数量繁多而且也比较简单，这里不一一列出.

系统流图中有2 个关键的速率方程:污染治理速率方程与资金补偿速率方程.速率方程的建立一般是系统动力学模型中较难部分，笔者用微分方程的方法建立速率方程.

1.2.1 污染治理速率方程

假设对于某个试验生产区，按照传统的方法进行农业生产，这时产生的污染量记为xm，现采取措施对污染进行治理，譬如发展生态农业，假设污染治理率为r，这里r 称为固有污染治理率，表示污染治理的初期(理论上是x=0 时)的污染治理率.随着污染治理的进行，治理率r 会随着污染治理量x 的增加而下降.若将r 表示成x 的函数r(x)，则它应该是x 的减函数.考虑t 到t+Δt 时间内污染物的治理增量，有

令Δt →0，得到x(t)满足微分方程

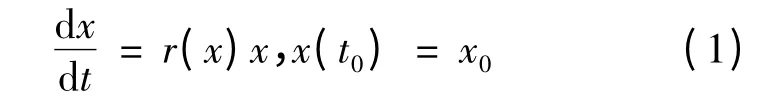
对于r(x)的一个简单假设是，设r(x)为x 的线性函数(工程师原则，首先用线性)，即

将式(3)代入微分方程(1)得

解微分方程(4)可得

即为污染治理速率方程.

1.2.2 资金补偿速率方程

同理，利用微分方程的理论，可以建立资金补偿速率方程，

式中:ym为最大补偿资金总量，由种植普通水稻的收益与种植有机水稻的收益的差值获得;y0为初始资金补偿量，由治理污染的固定成本以及初始污染治理量确定;r 为初始资金补偿率，由初始资金补偿量与最大资金补偿量确定.

2 流域农村面源污染生态补偿模型的实证研究

2.1 模型数据来源

通过对湖北省荆州市的实地考察调研，获取了模型基本数据，见表1.数据是在正常天气条件下以荆州市每亩的水稻为例，模拟上述模型获得.根据调研材料《荆州绿色农产品发展情况》，荆州市有机稻种植面积为2 000 亩.

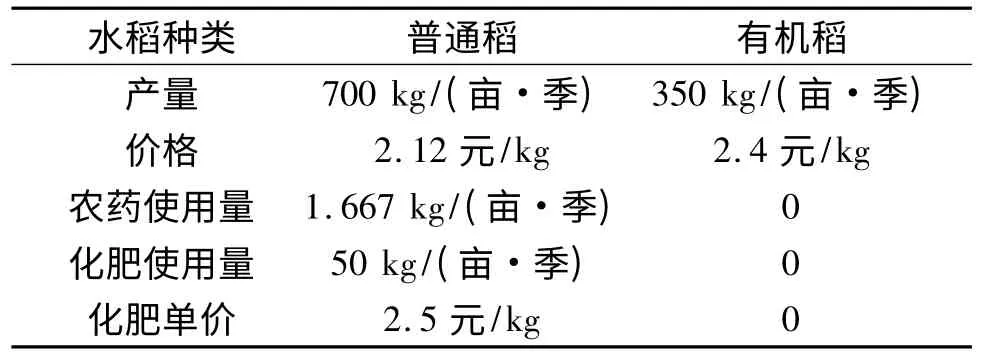
表1 模型数据

2.2 模拟结果分析

利用本模型模拟了时间期限100 a(1 200 月)污染治理量以及资金补偿总量，基准年为2010 年.最大污染治理量就是化肥使用量，这里取表1 中的数据50 kg/(亩·季);初始污染治理量可视作开始污染治理第一季时污染治理的数量，亦即第一季化肥使用的减少量;化肥单价、普通水稻单价等数据均取自表1.

2.2.1 污染治理总量的模拟结果及分析

当初始污染治理量分别取1，2，3 kg 时，利用Vensim 软件可得污染治理总量随时间变化的趋势，如图3 所示.

从图3 可以看出，污染治理总量曲线先单调增加，然后趋于平缓.随初始污染治理量的上升，污染治理总量急剧上升.初始污染治理量若为1 kg，治理时间为100 a (1 200 月)时，污染治理量远远未达到最大污染治理量50 kg;初始污染治理量提高到2 kg，大概在100 a(1 200 月)时，污染治理总量几乎达到了50 kg;初始污染治理量进一步提高到3 kg时，大概在840 月(70 a)，污染治理总量几乎达到50 kg.

图3 污染治理总量的变化趋势

表2 给出了污染治理的初始时刻到60 月时，每隔12 月的污染治理总量的变化.初始的污染治理量分别是1，2，3 kg.

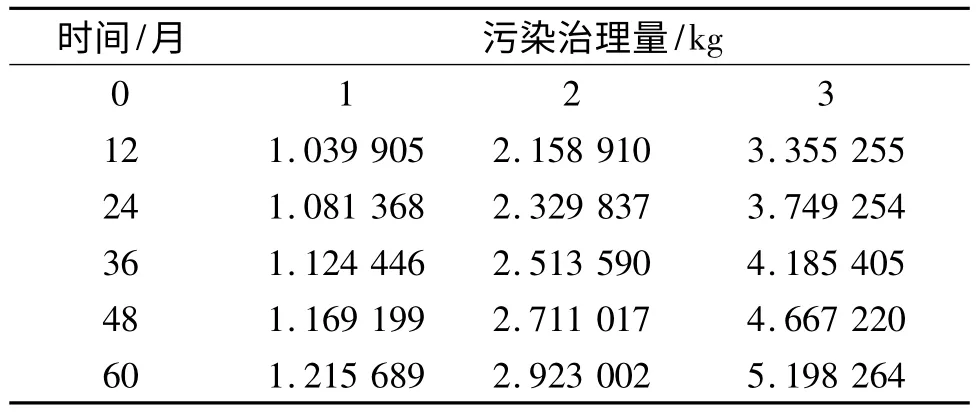
表2 污染治理总量的模拟结果

在污染治理的初始时刻，污染治理量分别为1，2，3 kg，而在60 月时，污染的治理总量分别达到了1.215 689，2.923 002，5.198 264 kg.由此可见，污染的初始治理量决定了治理的效果，在污染治理的后期，初始污染治理量为3 kg 时治理的污染几乎是初始污染治理量为1 kg 时的5 倍.污染治理的效果随着时间的增加更加明显，所以应该在污染治理的初期增加投入，提高污染治理量.

2.2.2 资金补偿总量的模拟结果及分析

当初始污染治理量分别取值1，2，3 kg 时，利用Vensim 软件得到资金补偿总量随时间变化的趋势，如图4 所示.

图4 资金补偿总量的变化趋势

由图4 可知，初始污染治理量大时，补偿的资金较多.这意味着污染治理需要专项经费做保障，生态基金的建立将有效地治理污染.另外，初始污染治理量为3 kg 时，资金补偿总量的曲线在治理的前期上升较快，后期逐渐平缓，而随着时间的增加，三者的资金补偿量将趋于一致.这说明在污染治理的后期，不管初始污染治理量为多少，补偿的资金都趋于稳定且一致.

表3 给出了初始污染治理量分别为1，2，3 kg时，从污染治理的初始时刻到60 月，每隔12 月的补偿资金的模拟结果.

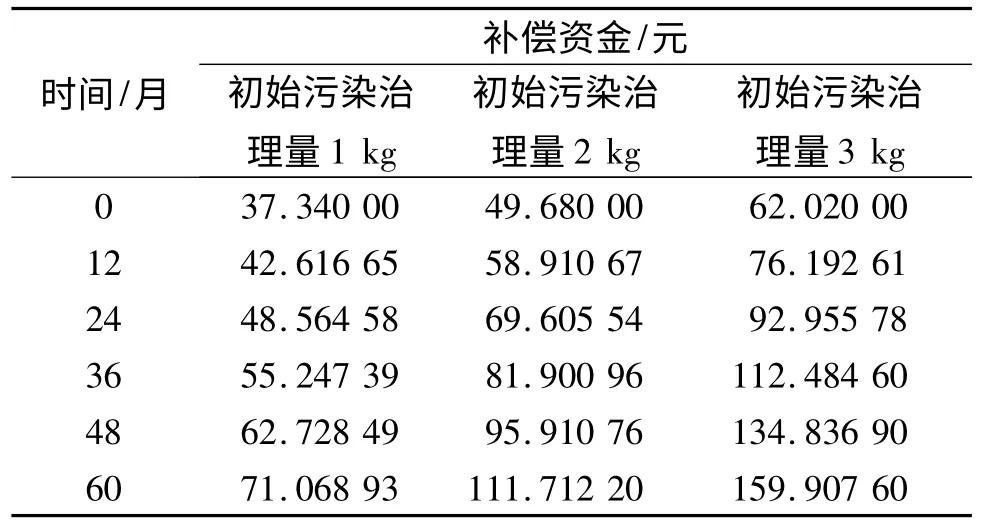
表3 资金补偿总量的模拟结果

从表3 可以看到，在初始时刻，污染的治理量由1 kg 提高到2 kg 时，补偿资金由37.34 元提高到49.68 元，增加了33.05%;污染治理量提高到3 kg时，补偿资金为62.02 元，相对于污染治理量1 kg时增加了66.09%.

2.2.3 资金补偿总量与污染治理总量的关系

当初始污染治理量分别为1，2，3 kg 时，利用Vensim 软件得到资金补偿总量与污染治理总量的关系，如图5 所示.

图5 资金补偿总量与污染治理总量的关系

图5 中，代表初始污染治理量为1 kg 时的曲线在最上方，说明初始污染治理量低的资金补偿总量反而高.导致该结果的原因是:初始污染治理量较小时，治理的速率低，花费的时间多，增加了时间成本，如果治理同样多的污染，初始污染治理量较小时所需资金补偿总量较多.

3 结论

综上可知，加大污染治理初期的投入，提高污染初期的治理量是提高污染治理效果的关键.初始投入少，初始污染治理量少，在后期看来，不但效率低下而且也不能节省资金.另外，污染的治理需要有专项资金如生态基金作为保障，增加污染初期治理的投入，治理污染将事半功倍.生态基金的来源不仅仅是政府为主导的一元化投入，还有生态基金投入的生态养殖、生态农业、生态渔业、生态旅游和垃圾回收带来的收益，从而实现“四湖”流域农村经济发展与污染治理的良性循环与可持续发展.

值得说明的是，该模型还可以用于分析其他的辅助变量取值变化所产生的影响，譬如有机稻价格的增加对污染治理的影响等，而且不必改变模型结构，只需改变相应辅助变量的取值，利用Vensim 软件即可获得相应结果，这也是利用系统动力学方法分析生态补偿问题的优势所在.由于数据缺乏，该模型的建立是在一定的假设下进行的，但是利用系统动力学方法是研究流域农村面源污染的多元生态补偿问题的一个新思路.事实上，如果图1 中所有变量的数据均可获得，图1 可以作为系统流图，相关的方程均可建立，也可以利用Vensim 软件进行模拟分析，模拟结果将更接近现实.不足之处在于实证分析只模拟了单纯的化肥造成的污染，而现实情况则比较复杂.

4 政策建议

保护水资源，任重而道远，需要近期手段和远期措施并重，常抓不懈.通过模拟分析可以看出，流域农村面源污染的管理重在公共治理机制的建设和发挥.面源污染防治资金的短缺，单靠政府、企业、居民任何一方都难以完全解决，建议流域所在地的政府引入多元的生态补偿机制:财政补贴一部分，生产者承担一部分，消费者补偿一部分，长期措施与短期措施并重，具体措施如下.

1)政府利用财政与金融手段提高环保投资的回报率，譬如提供低息贷款.

2)培育市场机制，譬如有机农药和化肥的规模使用以降低成本.

3)生态农业产业化，完善绿色农产品认证和标识工作，譬如普及绿色农产品质量认证.

4)成立专项基金——生态基金，从而保证多元补偿措施的实施.

5)数据的缺乏使相关研究难以展开，应在生态补偿措施实施过程中注意收集数据，建立数据库.

［1］毛显强，钟瑜，张胜.生态补偿的理论探讨［J］.中国人口·资源与环境，2002，12(4):38－41.

［2］郑海霞.中国流域生态服务补偿机制与政策研究［M］.北京:中国经济出版社，2010.

［3］陈兆开，施国庆，毛春梅.流域水资源生态补偿问题研究［J］.科技进步与对策，2008，25(3):56－60.

［4］周大杰，董文娟，孙丽英，等.流域水资源管理中的生态补偿问题研究［J］.北京师范大学学报:社会科学版，2005(4):131－135.

［5］王其藩.系统动力学(修订版)［M］.北京:清华大学出版社，1994.

［6］贾仁安，丁荣华.系统动力学－ 反馈动态性复杂分析［M］.北京:高等教育出版社，2002.

［7］王建华.SD 支持下的区域水资源承载力预测模型的研究［D］.北京:中国科学院地理科学与资源研究所，2000.

［8］李林红.滇池流域可持续发展投入产出系统动力学模型［J］.系统工程理论与实践，2002，8(8):89－94

［9］车越，张明成，杨凯.基于SD 模型的崇明岛水资源承载力评价与预测［J］.华东师范大学学报:自然科学版，2006(6):67－74.

［10］吴九红，曾开华.城市水资源承载力的系统动力学研究［J］.水利经济，2003，21(3):36－39.

［11］牛志强，王延辉，刘明珠.河南省水资源承载能力系统动力学模型及其应用［J］.水电能源科学，2009，27(1):48－50.

［12］李俊玲，袁连冲，钱自立.系统动力学在需水量预测中的应用［J］.人民长江，2008，39(2):20－22.