求解旅行商问题的分布式演化算法

韩 珂，杨俊鹏

(1.华北水利水电大学，河南 郑州 450045;2.中原工学院，河南 郑州 450007)

旅行商问题(Traveling Salesman Problem，TSP)是一类典型的NP 安全问题，也是数学领域的著名问题之一.该问题假设有一个旅行商人要拜访N 个城市，他从A 城出发，选择所要走的路径，要求N 个城市只能拜访一次，而且最后返回A 城.他可以有很多种走法，但是为了省时省力，他要选择一条最短的路径，TSP 问题就是用来求得的路径之路程为所有路径之中的最小值［1］.TSP 问题的术语描述:即寻找一条最短的遍历N 个城市的路径.用演化算法求解TSP 问题一直是学术界研究的热点，演化算法最引人注目的的特性是它的本质并行性［2］，对于规模较大的TSP 问题研究采用并行演化算法求解显得尤为重要.

目前的求解TSP 问题的演化算法普遍使用杂交算子为主算子，变异算子作为辅助算子，但是杂交算子涉及到群体中个体间信息的交换，而这可能增加处理机间的通信开销，所以属于不太适合并行计算的算子.其次，分布在各个处理机上进行演化的个体，在每演化了一万多代后，才进行一次处理机间的通信，这样就使通信开销在并行计算时间上所占的比例大大减少.最后，算法的串行计算部分所占的比例很小，当并行演化一万多代后，才收集所有的个体进行一次演化和淘汰操作.

笔者研究了一种并行计算演化算法来求解TSP问题.算法采用变异算子对每个个体进行独立的遗传操作，大大提高了算法的并行程度.该算法结构简单，采用主–从分布式并行模式，大量的演化操作由从进程完成，主进程只完成任务的分发和少量的遗传操作.算法选用通用的 TSPLIB 中的实例KROB150(这里KROB150 是设计实例为了验证算法的可靠性)和文献［3］中提到的中国CHN144 城市实例进行算法测试.对于实例KROB150，TSPLIB提供最短路径值为26 130(整数运算所得的结果)，文献［4］给出的最优路径值为26 127.357 9(浮点运算所得的结果)，笔者提出的算法所得的结果为:整数运算所得的结果为26 130，浮点运算所得的结果为26 127.357 888 739 3.对于CHN144 实例，文献［3］和［4］给出的最优路径值都为30 354.3(浮点运算所得的结果)，本算法所得的结果:浮点运算所得的结果为30 353.860 996 523 6，整数运算所得的结果为30 347.通过本算法得到的实际浮点运算值比参考文献［4］提出的值更优.

1 求解TSP 问题的并行演化算法

1.1 算法采用的变异操作

在算法上，设计的编码方式用普通路径来表达，一个染色体表示一次旅行.这种变异操作编码方式的特点是:变异算子的设计相对容易，计算个体的适应值无需解码.

由于引入了染色体编码，常规的变异算法在编码串中的异位发生突变情况下不再适用，所以这里需要采用基于位置的变异和基于次序的变异.首先考虑基于位置的变异，对个体编码串中随机选取的子串以逆转概率逆向排序后产生新的个体，这种倒位变异算子符合本编码模型的设计需求.其次是次序的变异，相对于位置的变异，只改变子串的一个位置利用插入的手段产生新个体，这样的插入变异算子设计更简单，同时也符合模型的变异算法.

倒位变异算子，是指在个体编码串中随即选取2 城市，使第1 个城市的右城市与第2 个城市之间的编码倒序排列，从而产生1 个新的个体.在父体中随机选择两个截断点，然后将两点间的城市反序，倒位算子是对染色体的边改动最少的变异(只变化了2 条边).

插入变异算子，是在父体中随机选择1 个城市，然后将这个城市随机插入到父体中的某个位置，该算子只变化了3 条边.

算法在这2 个变异算子的基础上设计了一个新的变异算子——组合变异算子.假设父体是S，组合变异算子操作步骤如下.

第1 步:从S 中任选2 个城市i 和j.

第2 步:假如将包含i 和j 在内的i 和j 间的所有城市反序后，使S 的适应值增加了，则将i 和j 间的城市做反序处理，同时修改S 的适应值.

第3 步:在S 中随即选择某个城市i，再在S 中任意选择另外1 个城市j.

第4 步:如果将i 放到j 的前面能使S 的适应值增加，则将该i 放到j 的前面，同时修改S 的适应值.

从以上操作过程可以看到，组合变异算子的特点如下.

1)该算子作用后，所得后代的适应值大于等于其父体的适应值，是一种无退化的变异.

2)当第2 步和第4 步中的条件都不满足时，有可能对父体没有改变.

3)该算子操作完后，所得后代的适应值也同时计算出来了.

算法将组合变异算子作为主搜索算子，用于局部区域的搜索.将一般的插入变异算子作为从变异算子，用于搜索方向向其他区域的迁移，跟组合变异算子一样，本算法让插入变异算子在变异的同时，修改个体的适应值.

1.2 求解TSP 的串行演化算法

PROCEDURETSP_GA

begin

optimal_indi :=M 中最佳的个体;

i:=0;gen:=0;

if gen＜=KS do

begin

if i＜=RG

begin

对M 中的每一个个体使用组合变异算子进行变异;

i:=i+1;

end

else

begin

if M 中最佳个体好于optimal_indi

optimal_indi:=M 中最佳的个体;

S:={从M 中选择的N－1 个个体};

M:=S+{个体optimal_indi};

对M 中的每一个个体使用插入变异算子进行变异;

i:=0;

gen:=gen+1;

end;

end;

end;

算法中的参数为每一轮使用组合变异算子进行变异的代数，为轮换次数，为群体规模.

1.3 并行演化算法

开始;

向PVM 提出登记;

创建从进程;

初始化群体M;

计算M 中个体的适应值;

optimal_indi:=M 中最佳的个体;

设gen:=0;

if gen＜=KS then

begin

将M 中所有的个体传给每个从进程;

然后等待接收所有从进程发来的新个体;

M:={接收到的N 个新个体};

if M 中最佳个体好于optimal_indi

将M 中最佳的个体赋予optimal_indi;

S:={从M 中选择的N－1 个个体};

M:=S+{个体optimal_indi};

gen:=gen+1;

end;

将进程终止条件发布给各从进程;

退出PVM;

end;

开始m 个从进程:

begin

返回并向PVM 登记;

repeat

按序号接收主进程传来的个体;

S:={接收到的个体};i:=0;

if i＜=RG then

begin

对S 中的每一个个体使用组合变异算子进行变异;

i:=i+1;

end;

将S 中的个体依次传递给主进程;

满足终止条件(gen＜=KS);

退出PVM.

2 算法说明与分析

本算法与传统的全局单种群主－从模式(主程序存储整个种群)有所不同，采用“主－ 从编程模式”，即1 个主进程控制并协调多个从进程.由从程序来评估个体的适应值，个体的适应值评估是并行的，适应值的评估在程序中花费时间最长.

算法中使用了KS，N，RG 3 个参数:参数KS 用来控制整个算法的终止.算法经过反复执行轮的过程，经过KS 轮的操作后，最终找到最优解.这里的“轮”是指让群体进化指定的数，通过竞赛选择机制淘汰较差的个体，再对剩余的每一个个体进行一次插入变异，这个过程称为1 轮.参数N 用来表示群体的规模.参数RG 用来表示每一轮中使用组合变异算子演化.

从求解TSP 问题的算法看出，变异后的个体适应值只需在原适应值的基础上稍作计算，变异算子最多改动一个个体的3 条边，所以花费在这里的计算时间较短.但是一旦求解问题的规模N 增加，染色体的长度增加，倒位和插入所移动的城市的总数将增加，遗传操作花费时间将快速增长.由于上述原因，算法在设计时，将大部分遗传操作放到从程序中执行，遗传操作和个体的评估并行执行，当从进程执行后，才执行RG 个体的遗传操作并计算适应值.

下面分析一下算法的加速比.

设处理机的台数为i.从以上算法可看出，算法每执行1 轮，进行1 次处理机通信，设这个通信时间为TC.串行算法执行的每1 轮中，可设并行部分的计算时间为TP，串行部分的执行时间为TS，因为在每1 轮中使用组合变异算子进行RG 代演化后(可并行部分)，才进行选择操作和一代插入变异(需串行的部分)，所以可认为TP=RG×TS.则进行每一轮演化，采用串行计算所需的总时间为

采用并行计算所需的总时间为

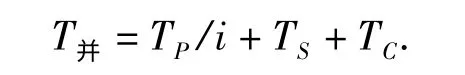
则加速度比为

从上式看出，i 越大，λ 越大;RG 越大，λ 也越大.但RG 过大会影响解的质量，因为RG 过大，在相同运算的时间内，KS 会减少，进行搜索方向迁移的次数会减少，就有可能发生过早收敛;RG 过小，在局部区域搜索的时间就会减少，使解的精度降低.在实例测试中，取RG=18 000.当问题的规模增大(城市的个数增多)时，因为TP的增长幅度远大于TC，所以λ 也增大.

从以上分析可看出，该算法特别适合大规模的TSP 问题的并行演化计算，且机器越多越好，当问题的规模相当大时，甚至可以让一台处理机只处理一个个体.

3 算法测试

1)参数设定.算法测试所设定的参数为:RG=20 000，N=50;测试实例为选择TSPLIB 中的150 个城市解决TSP 问题，命名为KROB150;选择中国144个城市解决TSP 问题，命名为CHN144.

2)实验情景.实验主要模拟网络环境，并行计算机的运作方式，将网络中每台计算机安装PVW运算环境，同时使用6 台计算机，每台计算机只运行一个进程.对每个问题进行浮点运算和整数运算，每组20 次.计算数值见表1.

表1 算法求得最优值

表1 中整数运算是指根据城市的原始坐标值计算出来的所有的2 个城市间的距离值四舍五入取整运算.浮点运算是指保留小数位运算.

假定算法找到上表中的最优解时终止，记录算法运行的时间及最优解的首达时间.串并行演化算法所用的时间对比见表2—3.

表2 CHN144 串并行演化时间对比 s

表3 KROB150 串并行演化时间对比 s

假设当算法找到上述表格中的最优解时停止.表2 和表3 的数据显示，用串行演化算法的平均时间较长，是并行演化算法的平均时间的3 倍.让串行演化算法和并行演化算法演化相同的轮数终止，串行演化算法的平均时间是并行演化算法的平均时间的2.89 倍，并行演化算法取得了较好的加速比.

4 结语

并行演化算法使用了较少的参数，只使用了变异算子，提出的组合变异算子具有很强的搜索能力;平均计算时间不到1 min，取得了较好的加速比;具备收敛速度快、解精度高等特点，实验的结果都接近或优于已知最优解.

笔者将在此基础上，进一步研究算法中参数RG(每1 轮进化的代数)与问题的规模之间的关系，并对并行演化算法的计算效率做深入研究.

［1］Garey M R，Johnson D S.Computers and intractability［D］.San Francisc:Bell Telephone Laboratories，1979.

［2］Zbigniew Michalewicz.Genetic Algortihms+Data Structures=Evolution Programs［M］.Berlin Heidelberg:Springer-Verlag，1996.

［3］康立山，谢云，尤失勇.非数值并行运算法:模拟退火算法［M］.北京:科学出版社，1997

［4］吴斌，史忠植.一种基于蚁群算法的TSP 问题分段求解算法［J］.计算机学报，2001，24(12):1328－1333.