考虑应力敏感时的煤层气压裂滤失量计算

李 亭, 杨 琦, 牛建兵, 杨 波, 冯文光

(1.成都理工大学 能源学院，成都 610059; 2.中国石油 渤海钻探井下技术服务公司，天津 300283)

考虑应力敏感时的煤层气压裂滤失量计算

李 亭1, 杨 琦1, 牛建兵2, 杨 波1, 冯文光1

(1.成都理工大学 能源学院，成都 610059; 2.中国石油 渤海钻探井下技术服务公司，天津 300283)

由于煤层天然裂缝发育、对应力敏感以及煤岩较软、易碎等因素，造成煤层气压裂滤失量较大，常用的Carter计算滤失的方法已经不再适用。针对这一问题，作者考虑裂缝内的压力与地层压力之间的压差，对煤层渗透率和孔隙度的影响，并根据相应的计算方法，在Carter方法的基础上对其中的滤失系数进行修正，可以计算出综合滤失系数和滤失量。通过计算实例，并与Carter计算结果进行对比，表明本文所提出的方法比较符合实际。

煤层气；水力压裂；滤失模型；计算方法

压裂液滤失系数的计算或评价，主要有3种方法：利用滤失理论进行计算；通过岩心动态或静态滤失实验确定；主压裂前进行小压测试分析来确定滤失系数[1]。对于煤层气压裂滤失量的计算，还没有比较有效的方法。这主要是由于煤层天然裂缝发育，对应力敏感以及煤岩较软、易碎等因素造成难以准确计算滤失量。由于煤层压裂滤失量比较大，经常会超过所造裂缝体积，因此压裂液效率比较低。准确计算压裂液的滤失量[2,3]，对于压裂效果的评价分析和裂缝几何尺寸的确定，十分关键。对于煤层气压裂，计算压裂液滤失系数的Carter经典方法，已经不再适用。本文针对煤层气压裂的特点，综合考虑压裂过程中压力对煤岩渗透率和孔隙度的影响，提出一种新的计算方法，并进行了实例计算和相应的对比分析。

1 计算模型

由于目前煤层气压裂，多采用活性水或清水作为压裂液，并不产生滤饼，因此，在滤失系数计算时，只考虑压裂液和地层水的黏度与压缩系数对滤失的影响。

1.1 基本假设

假设：(1)煤层上下顶底板的地应力均高于煤层的地应力，裂缝高度受限在煤层内，裂缝长度在煤层内延伸；(2)压裂过程中，压裂液沿裂缝壁面垂直滤失；(3)随着裂缝长度的增加，裂缝内压力不断减小，直至裂缝不再延伸时，缝端部压力为零；(4)裂缝几何形状和延伸符合PKN模型。

取裂缝半长，几何模型见图1。

在裂缝长度方向上，划分不同的长度段，即对应着不同的时间段。在每一小段内，取平均压力，分别计算其滤失量，然后累加，计算出裂缝长度上的滤失量。考虑到离井筒越近裂缝内的压力梯度越大，为提高计算滤失量的准确性，采用不均匀分割方式。在距离井筒较近处，每段的长度较小，随着裂缝的延伸，划分的每段长度逐渐增大。

图1 滤失计算几何模型

1.2 裂缝长度与泵注时间和净压力的关系

裂缝长度与泵注时间成一定的比例关系[4-6]

(1)

式中：x为从井筒至裂缝上某点的距离(m);l为裂缝长度(m);t为裂缝上某点张开的初始时间(min);tp为整个压裂过程的泵注时间(min);n为指数，介于0.5～1之间。

裂缝内净压力的计算公式为

(2)

式中：pnet为裂缝内净压力(MPa);ηa为压裂液黏度(mPa·s);qi为注入排量(m3/min);G为平面剪切模量(MPa);h为裂缝高度(m);l为裂缝长度(m)。

裂缝上的li段所对应的压差，取i-1和i两点压差的平均值，则有

Δpi,net=(p(i-1),net+pi,net)/2

(3)

Δpi=Δpi,net+pc-p

(4)

式中：Δpi,net为li段内的平均净压力(MPa);p(i-1),net为裂缝内i-1点的净压力(MPa);pi,net为裂缝内i点的净压力(MPa); Δpi为li段内的平均压力与地层压力之差(MPa);pc为地层裂缝闭合压力(MPa);p为地层压力(MPa)。

1.3 总的滤失量

整条以井筒为中心对称的裂缝，总的滤失量为

(5)

式中：Q为整条裂缝上的滤失量(m3);li为裂缝半长上的小段长度(m);Ci为裂缝上li段所对应的综合滤失系数(m/min0.5); Δti为裂缝上li段所对应的滤失时间(min)。

在裂缝上li段，所对应的综合滤失系数Ci可由下式计算

(6)

(7)

(8)

式中：Ci1为受压裂液黏度控制、对地层渗透率敏感的滤失系数(m/min0.5);Ci2为受地层流体压缩性控制、对地层渗透率敏感的滤失系数(m/min0.5);K为动态渗透率(10-3μm2);φ为地层孔隙度(%);Cw为煤层孔隙内流体的压缩系数(MPa-1，假设煤层饱和地层水，煤层内的流体即为地层水);η为地层流体黏度(mPa·s)。

裂缝上li段所对应的滤失时间Δti为

Δti=tp-ti

(9)

式中：ti为裂缝上li段张开的初始时间(min) 。

2 压力对滤失的影响

2.1 煤层动态渗透率的计算

由于煤层一般比较松软、易碎，天然裂缝系统比较发育，因此煤层渗透率对应力的变化非常敏感。根据国内外的研究[7,8]发现，煤层渗透率与地层净应力的关系呈指数递减规律，即

K=K0e-3Cf(σ-σ0)=K0e-3CfΔσ

(10)

式中：K为煤层应力改变后的动态渗透率(10-3μm2);K0为初始应力下的渗透率(10-3μm2);σ为改变后的应力(MPa);σ0为初始应力(MPa); Δσ为煤层有效应力的变化值(MPa);Cf为煤层天然裂缝系统的压缩系数(MPa-1)。

上述计算动态渗透率的经验公式由McKee提出[8]，通过实验和现场实践，已经得到普遍认可。该公式适用于水力压裂和压后生产过程中动态渗透率的计算。

煤层天然裂缝系统的压缩系数比较难确定，需要通过岩心实验测试不同有效应力下的压缩系数，然后再进行拟合，或者通过干扰试井测试得到。

煤层的净围压等同于作用在煤层上的有效应力，由下面的公式[9,10]计算

σe=σv-βp

(11)

式中：σv为地层垂直方向上的应力(MPa);β为Biot常数(约为1)。

在对煤层气井进行压裂施工时，随着压裂液的注入，地层孔隙压力增大，引起地层有效应力的改变。此时，作用在煤层上的有效应力与此前作用在煤层上的净围压，两者方向相反，因此，压裂施工会导致煤层渗透率增大，滤失速度变大。有效应力的变化如下

Δσ=(σv-βpf)-(σv-βp)=β(p-pf)

(12)

式中：pf为压裂施工时裂缝内的压力(MPa)。

压裂施工时的动态渗透率为

K=K0e-3CfΔσ=K0e3Cfβ(pf-p)

(13)

2.2 压力对孔隙度的影响

孔隙度与压力、裂缝系统体积压缩系数三者的关系，由下式给出

由此可得

Δφ=CfΔpφ

φp=φ(1+CfΔp)

(14)

式中：φp为压力改变后的孔隙度(%); Δp为压力改变值(MPa)。

3 计算实例

某煤层气井基本参数如下：煤层温度为30℃，煤层压力为7.55 MPa，煤层渗透率为1.48 ×10-3μm2，孔隙度为1%，地层流体黏度为1.05 mPa·s，地层水的压缩系数为0.000 485 MPa-1，天然裂缝系统的压缩系数为0.068 MPa-1，地层裂缝闭合压力为15.326 MPa。

施工参数：压裂液为活性水，黏度为1.25 mPa·s。压裂施工时，井底压力为25.785 MPa，注入排量6.0 m3/min，前置液120 m3，携砂液180 m3，泵注时间54 min。裂缝长度136 m，高度8.5 m。具体计算结果见表1。

如果不考虑应力对渗透率和孔隙度的影响，按照Carter公式，可以计算出裂缝长度上每一段的滤失系数和累计滤失量，与动态结果对比，具体见图2、图3。可以看到，由于煤层渗透率和孔隙度对应力比较敏感，造成滤失系数对应力非常敏感。井底压力与地层压力之间的差值越大，动态滤失系数越大，与Carter公式计算出的滤失系数相差也就越大。这样，在考虑应力影响时，动态滤失量要明显大于Carter公式计算出的静态滤失量，因此，在煤层气压裂时，一定要考虑应力的影响；否则，模拟出的裂缝几何尺寸和形态会与实际情况有较大差别。

4 结论与认识

考虑煤层对压力的敏感，根据压裂施工时井底压力和沿缝长方向上裂缝内压力的变化，计算出动态渗透率和动态孔隙度，进而计算出对应的动态滤失系数，提高了所计算滤失量的准确性。

沿裂缝长度方向，划分不同的长度单元，分别计算相应的滤失系数和滤失量，最后累加，计算出整个缝长上的滤失总量。

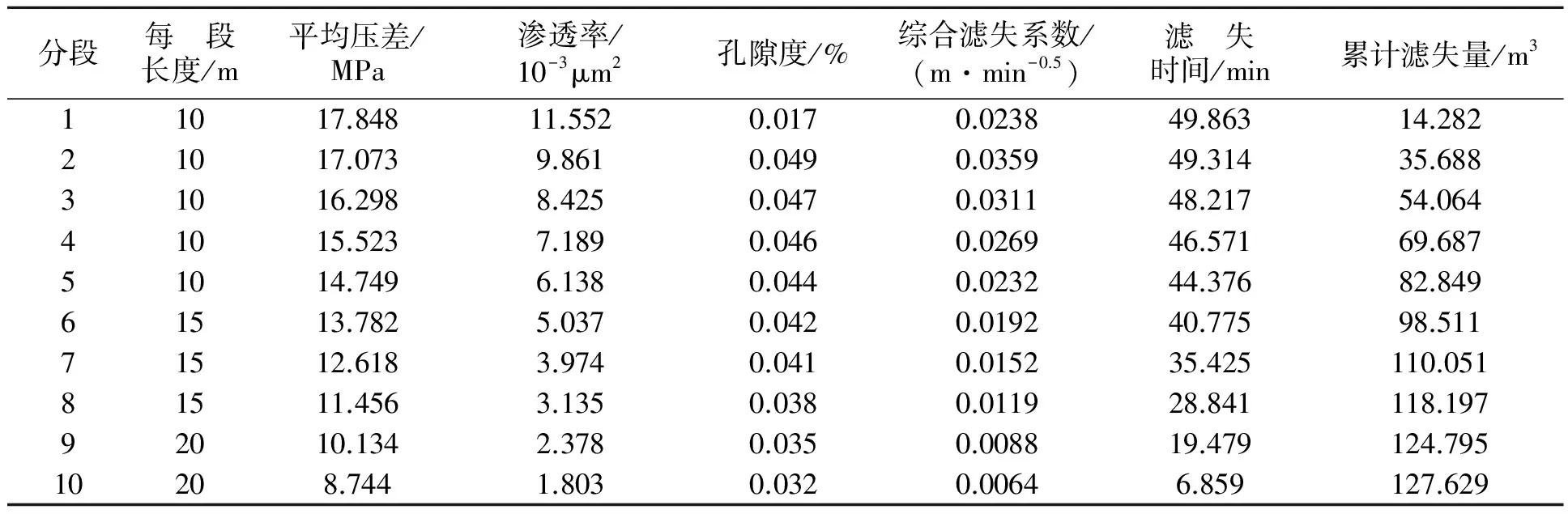
表1 应力影响下的动态滤失系数和滤失量计算结果

图2 综合滤失系数对比图

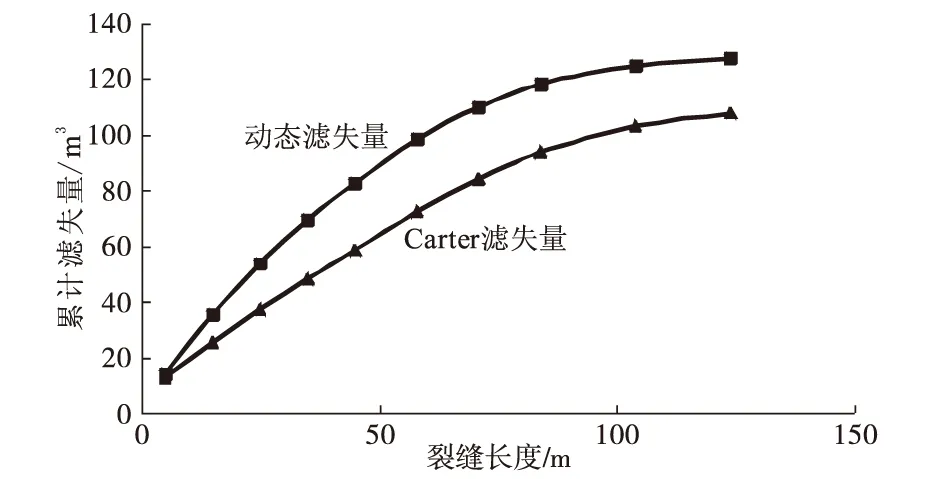
图3 累积滤失量对比

结合实例，计算出了煤层气井压裂滤失总量，并和常用的Carter滤失计算方法做了对比，表明本文的计算方法较为符合实际。

煤层气压裂时，要考虑应力对煤层渗透率和孔隙度的影响；否则，滤失量和裂缝几何尺寸的模拟计算结果会与实际相差较大。

[1]Yi T C, Peden J M. A comprehensive model of fluid loss in hydraulic fracturing [J]. SPE, 1994, 22(11): 267-272.

[2]席先武,郑丽梅.煤层压裂液滤失系数计算方法探讨[J].天然气工业,2001,21(3):45-47.

Xi X W, Zheng L M. A discussion on the methods of calculating filtration coefficient of fracturing fluid in coal-bed [J]. Natural Gas Industry, 2001, 21(3): 45-47. (In Chinese)

[3]宋佳，卢渊，李永寿，等.煤岩压裂液动滤失实验研究[J].油气藏评价与开发，2011,1(1/2):74-77.

Song J, Lu Y, Li Y S,etal. Experiment research on fracture fluid dynamic filtration of coalrocks[J]. Reservoir Evaluation and Development, 2011, 1(1/2): 74-77. (In Chinese)

[4]蒋廷学，汪绪刚，冯兴凯，等.压裂施工中对地层滤失性的现场评价[J].石油钻采工艺，2002,24(2):78-79.

Jiang T X, Wang X G, Feng X K,etal. The Site Evaluation for the leak-off property of formation during fracturing operation[J]. Oil Drilling & Production Technology, 2002, 24(2): 78-79. (In Chinese)

[5]Sparks D P, McLendon T H. The effects of stress on coal-bed reservoir performance, Black Warrior Basin, USA [J]. SPE, 1995, 23(10): 22-25.

[6]冯利娟, 郭大立，曾晓慧，等．煤层应力敏感性及其对压裂液滤失的影响[J].煤田地质与勘探,2010,38(2): 14-18.

Feng L J, Guo D L, Zeng X H,etal. Experimental study on the stress sensitivity of coal and its impact on the filtration of the fracturing fluid[J]. Coal Geology & Exploration, 2010, 38(2): 14-18. (In Chinese)

[7]李勇明，赵金洲，郭建春，等.裂缝性低渗透储层压裂液滤失计算新模型[J].石油钻采工艺，2004,26(5):44-46,49.

Li Y M, Zhao J Z, Guo J C,etal. New model of the filtrate loss of fracturing fluid in naturally fractured and low permeability formation [J]. Oil Drilling & Production Technology, 2004, 26(5): 44-46,49. (In Chinese)

[8]曾晓慧，郭大立，王祖文，等．压裂液综合滤失系数的计算方法研究[J].西南石油学院学报,2005,27(5)：53-56.

Zeng X H, Guo D L, Wang Z W,etal. The research on computed methods of leak-off coefficient for fracture fluid [J]. South West Petroleum Institute Journal, 2005, 27(5): 53-56. (In Chinese)

[9]时伟.浅析煤储层压裂缝滤失系数的计算[J].科技情报开发与经济，2010,20(15)：145-146.

Shi W. Analysis on the calculation of leak-off coefficient of coal reservoir’s pressing-crack[J]. Sci-tech Information Development & Economy, 2010, 20(15): 145-146. (In Chinese)

[10]李勇明，王中武，郭建春，等.天然裂缝开启前后的煤层压裂液滤失计算[J].油气井测试，2006,15(1):8-9,12.

Li Y M, Wang Z W, Guo J C,etal. Calculation of fracturing fluid leak-off in coal bed with reopened natural fractures[J]. Well Testing, 2006, 15(1): 8-9,12. (In Chinese)

Leak-offcomputationofhydraulicfracturingincoal-bedmethaneunderconsideringstresssensitivity

LI Ting1, YANG Qi1, NIU Jian-bing2, YANG Bo1, FENG Wen-guang1

1.CollegeofEnergyResources,ChengduUniversityofTechnology,Chengdu610059,China;2.Down-holeServiceCompany,CNPCBohaiDrillingEngineeringCompanyLimited,Tianjin300457,China

Because of the influencing factors, such as the existing of natural fractures, the stress sensitivity, the softness and frailty of the coal formation, the leak-off volume is great in the hydraulic fracturing of coal-bed methane and the usual Carter’s calculating leak-off method has not been applicable. From the view that the pressure difference between fracture and formation affects severely the permeability and porosity of the coal formation, this paper provides a new mathematical model and the related calculation methods. Finally, one field case example is illustrated and compared with the Carter’s method. It is concluded that the new method is more applicable for the field situations.

coal-bed methane; hydraulic fracturing; leak-off model; computation method

10.3969/j.issn.1671-9727.2013.01.006

1671-9727(2013)01-0040-04

2012-07-10

国家科技重大专项(2011ZX05060-002)

李亭(1976-),男,博士研究生,研究方向:低渗透和非常规油气藏增产技术, E-mail:dragonlt@163.com。

TE132.2; TE357.1

A