拓扑动力系统中的强不变集*

耿雪萍，金渝光

(重庆师范大学 数学学院，重庆401331)

回归点、非游荡点、终于周期点和几乎周期点的概念都是由周期点的概念推广得到的，它们是动力系统中的重要概念.2011年孙长岭在文献［1］中讨论了在一般拓扑空间或序列紧拓扑空间中，周期点集、链回归点集和ω-极限点集是闭集且是强不变闭集.此处进一步证明在拓扑空间X中，f是同胚的，f(R(f))=R(f);f(Ω(f))=Ω(f);f(EP(f))=EP(f)f(AP(f))=AP(f)是成立的.

1 有关定义和引理

恒设X是拓扑空间，f:X→X同胚，x∈X.

定义1［2］x∈X称为f的周期点，如果存在整数n＞0，使得fn(x)=x，周期点的集合记为P(f).

定义2［2］x∈X称为f的回归点，如果对于x的任意领域U，存在整数n＞0，使得fn(x)∈U，回归点的集合记为R(f).

定义3［2］x∈X称为f的非游荡点，如果对于x的任意领域U，存在整数n＞0，使得fn(U)∩U≠∅，非游荡点的集合记为Ω(f)，x的领域的集合记为Ux.

定义4［4］x∈X称为f的终于周期点，如果∃n＞0，使得fn(x)∈P(f)，终于周期点的集合记为EP(f).

定义5［2］x∈X称为f的几乎周期点，如果对于x的任意领域U，∃N＞0，使得在连接着的N个数中总有某一个n适合fn(x)∈U，几乎周期点的集合记为AP(f).

定义6［2］Λ⊂X 称为 f的(强)不变集，如果 f(Λ)⊂Λ(f(Λ)=Λ).

引理1［3］设X是拓扑空间，f:X→X同胚，则f(P(f))⊂P(f).

2 命题

命题1 设X是拓扑空间，f:X→X同胚，则Ω(f)=Ω(f－1).

证明 (1)先证 Ω(f－1)⊂Ω(f).

∀x∈Ω(f－1)，由定义 3 得，∀U∈Ux，∃n ＞0，(f－1)n(U)∩U≠∅，即 f－n(U)∩U≠∅.于是∃y∈f－n(U)∩U，则y∈f－n(U)且y∈U，即有fn(y)∈U 且fn(y)∈fn(U).从而fn(y)∈fn(U)∩U，故fn(U)∩U≠∅，因此 x∈Ω(f).又由 x的任意性得，Ω(f－1)⊂Ω(f).

(2)再证 Ω(f)⊂Ω(f－1).

∀x∈Ω(f)，由定义3 得，∀U∈Ux，∃n ＞0，fn(U)∩U≠∅.于是∃y∈fn(U)∩U，则 y∈fn(U)且 y∈U，又由 f同胚，则有 f－n(y)∈U 且 f－n(y)∈f－n(U).从而 f－n(y)∈f－n(U)∩U，故 f－n(U)∩U≠∅，因此 x∈Ω(f－1).又由 x的任意性得，Ω(f)⊂Ω(f－1).

综上所述，Ω(f)=Ω(f－1).

3 定理及证明

定理1 设X是拓扑空间，f:X→X同胚，则R(f)是强不变集.

证明 要证R(f)是强不变集，即证f(R(f))=R(f).

(1)先证f(R(f))⊂R(f).

∀y∈f(R(f))，则存在 x∈R(f)，使得 f(x)=y.∀U∈Ux，由于 f是连续的，则 V=f(U)∈Uf(x).又因为 x∈R(f)，由定义2得，∀U∈Ux，存在整数 n＞0，使得 fn(x)∈U.因此对上述 n＞0，有 f°fn(x)∈Uf(x)，即 fn(f(x))∈Uf(x)，即有 fn(y)∈Uy，所以 y∈R(f).又由 y 的任意性得，f(R(f))⊂R(f).

(2)再证R(f)⊂f(R(f)).

∀x∈R(f)，因为 f是同胚的，所以 f－1连续，则∀U∈Ux，有 V=f－1(U)∈Uf－1(x).又因为 x∈R(f)，由定义2 得，∀U∈Ux，∃n ＞0，使得 fn(x)∈Ux.于是对上述∃n ＞0，有 f－1(fn(x))∈Uf－1(x)，即 fn(f－1(x))∈Uf－1(x)，则f－1(x)∈R(f)，得 x∈f(R(f)).又由 x 的任意性得，R(f)⊂f(R(f)).

综上所述，f(R(f))=R(f)，即R(f)是强不变集.

定理2 设X是拓扑空间，f:X→X同胚，则Ω(f)是强不变集.

证明 要证Ω(f)是强不变集，即证f(Ω(f))=Ω(f).

(1)先证 f(Ω(f))⊂Ω(f).

∀y∈f(Ω(f))，则存在 x∈Ω(f)，使得 f(x)=y.∀U∈Uf(x)，V=f－1(U)∈Ux.又因为 x∈Ω(f)，由定义 3得，存在整数n＞0，使得fn(V)∩V≠∅，从而

故f(x)=y∈Ω(f).又由y的任意性得f(Ω(f))⊂Ω(f).

(2)再证 Ω(f)⊂f(Ω(f)).

∀y∈f－1(Ω(f－1))，则存在 x∈Ω(f－1)，使得 f－1(x)=y.∀U∈Uf－1(x)，V=f(U)∈Ux.又因为 x∈Ω(f－1)，由定义3 得，存在整数 n ＞0，使得 f－n(V)∩V≠∅，从而

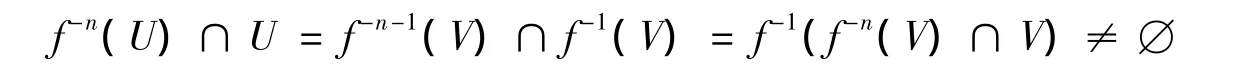
故 y=f－1(x)∈Ω(f－1)，由 y 的任意性得 f－1(Ω(f－1))⊂Ω(f－1)，由命题 1 得 f－1(Ω(f))⊂Ω(f)，所以Ω(f)⊂f(Ω(f)).

综上所述，f(Ω(f))=Ω(f)，即Ω(f)是强不变集.

定理3 设X是拓扑空间，f:X→X同胚，则EP(f)是强不变集.

证明 要证EP(f)是强不变集，即证f(EP(f))=EP(f).

(1)先证f(EP(f))⊂EP(f).

∀x∈f(EP(f))，则存在 y∈EP(f)，使得 f(y)=x.因为 y∈EP(f)，由定义 4 得，∃n ＞0，使得 fn(y)∈P(f).由f连续与引理1得，f°fn(y)∈f(P(f))⊂P(f)，即 fn(x)∈P(f).于是对上述的 n＞0，有 fn(x)∈P(f).从而x∈EP(f).又由x的任意性得，f(EP(f))⊂EP(f).

(2)再证EP(f)⊂f(EP(f)).

∀x∈EP(f)，由定义4得，∃n＞0，使得 fn(x)=z∈P(f).因为 z∈P(f)，由定义1得，存在整数 N ＞0，使得 fN(z)=z.从而 f－1(fN(z))=fN(f－1(z))=f－1(z)，故 f－1(z)∈P(f).于是对上述的 n ＞ 0，f－1(z)=f－1(fn(x))=fn(f－1(x))∈P(f)，则 f－1(x)∈EP(f)，因此 x∈f(EP(f)).又由 x 的任意性得，EP(f)⊂f(EP(f)).

综上所述，f(EP(f))=EP(f)，即EP(f)是强不变集.

定理4 设X是拓扑空间，f:X→X同胚，则AP(f)是强不变集.

证明 要证AP(f)是强不变集，即证f(AP(f))=AP(f).

(1)先证f(AP(f))⊂AP(f).

∀x∈f(AP(f))，则存在 y∈AP(f)，使得 f(y)=x.∀ε ＞0，∀y1∈Uy，由 f连续得，f(y1)∈Uf(y)=Ux.又因为y∈AP(f)，由定义5得，对于∀U∈Uy，∃N＞0，使得在连接着的N个数中总有某一个n适合fn(y)∈Uy.因此 f°fn(y)∈Ux，即 fn(f(y))=fn(x)∈Ux，所以 x∈AP(f).又由 x 的任意性得，f(AP(f))⊂AP(f).

(2)再证AP(f)⊂f(AP(f)).

∀x∈AP(f)，∃N＞0，使得在连接着的N个数中总有某一个n适合fn(x)∈Ux.∀ε＞0，∀y∈Ux，由f同胚得，f－1连续，则 f－1(x)∈Uy.因此 f－1(fn(x))=fn(f－1(x))∈Uy=Uf－1(x)，则有 f－1(x)∈AP(f)，所以 x∈f(AP(f)).又由x的任意性得，AP(f)⊂f(AP(f)).

综上所述，f(AP(f))=AP(f)，即AP(f)是强不变集.

［1］孙长岭.关于拓扑动力系统中的闭集和强不变闭集［J］.绵阳师范学院学报，2011，30(5):16-18

［2］熊金城.线段自映射的动力系统:非游荡集、拓扑熵及混乱［J］.数学进展，1988，17(1):1-9

［3］张伟年.动力系统基础［M］.北京:高等教育出版社，2001

［4］周作领.一维动力系统［J］.数学月刊，1988，3(3):43-47

［5］陈绥阳，褚蕾蕾.动力系统基础及其方法［M］.北京:科学出版社，2002

［6］李进金，李克典，林寿.基础拓扑学导引［M］.北京:科学出版社，2009

［7］周作领，易建东，徐绍元.拓扑动力系统:从拓扑方法到遍历理论方法［M］.北京:科学出版社，2011

［8］冉海全.关于度量空间中终于周期点集的注记［J］.湖北民族学院学报:自然科学版，2010，28(1):63-64

［9］关鹏，张海永，张荣.关于几乎周期点的讨论［J］.河南科技大学学报:自然科学版，2007，28(5):76-78

［10］邹成，赵清俊.渐近周期点的若干性状［J］.重庆工商大学学报:自然科学版，2011，28(2):142-144