四阶矩阵代数中两个新的Kadsin-singer格*
王 宁
(重庆师范大学 数学学院,重庆401331)
1 基本概念
经过一个多世纪的发展,von neumann代数的理论已经作为自伴算子代数理论的重要研究对象之一.为了研究有界线性算子的结构性质,如不变子空间的相关问题,Kadison和singer[1]平行于Von Neumann代数理论,引入了三角代数.2008年,葛力明和袁巍[2,3]将三角代数、自反代数和von Neumann代数理论相结合,引入了一类新的非自伴算子代数——Kadison-singer代数,简称KS-代数.KS-代数与Von Neumann代数之间的联系是通过不变投影格来实现的.这些投影格是自反的[4],且在生成KS-代数的对角子代数的意义下具有“极小性”.如果不变投影格中的所有投影是相互交换的,则称之为交换格.套代数是不变投影格为交换格的唯一KS-代数.因此,在这种意义下,KS-代数可以看成是“量子化”的套代数.
董瑷菊等[5]证明了在相似意义下分别生成von Neumann代数为M2(C)和M3(C)的KS-格M0是唯一的,即每个生成M2(C),M3(C)的KS-格都相似于M0或I-M0,M0是单点扩张下生成的M3(C)的KS-格.在此基础上,把这两种KS-格分别嵌入到M4(C)中,构成了生成von neumann代数为M2(C)⊕C⊕C和M3(C)⊕C的KS-格,并加以证明.
下面介绍所涉及的基本概念和符号.
令H为可分的复Hilbert空间,B(H)为H上的有界线性算子的全体.(B(H))是B(H)中的全体投影组成的集合.
设S为B(H)中的正交投影集,用A lg S表示使得S中每个投影都不变的有界线性算子的全体构成的代数,它是B(H)中一个弱算子的闭子代数,记为
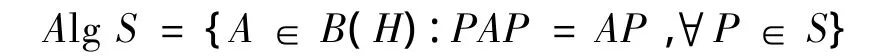
相应地,对于B(H)中的子集L,用Lat L表示L中的不变投影格,记为

在一般情况下,总有S⊆Lat A lg S和L⊆A lgLat L.
定义1 设A是B(H)的一个子代数,如果A=A lgLat A,则称A是自反代数.设L是B(H)的子空间格,如果L=Lat A lg L,则称L是自反格.
定义2 设N为Hilbert空间H上的一个投影集,如果N为全序集且包含0和恒等算子I,则称N为一个套,套具有自反性.N相应的不变子空间的格代数A lg N为套代数,由N生成的Von Neumann代数N″为套代数的核,称A lg N∩(A lg N)*为套代数A lg N的对角.
定义3 设A为B(H)中的子集,称A'={B∈B(H):AB=BA,∀A∈A}为A在B(H)中的交换子.A的二次交换子A″是A'的交换子,即A″=(A')'.
定义4 设M1和M2是作用在H上的两个投影格,若存在H上的可逆算子T,使得TM1=M2,则称M1和M2相似,其中TM1={Ran(TPT-1):P∈M1},Ran(A)表示算子A的值域投影,即H到A的值域闭包上的投影.
定义5 设L是B(H)的子空间格,E∈L,定义:

定义6 若B(H)的子代数A满足:
(1)A是自反代数.
(2)如果B(H)的自反子代数B包含A,即A⊆B,并且有B∩B*=A∩A*,那么A=B,则称A为Kadison-singer代数(或 KS-代数).
若KS-代数A的对角子代数A∩A*为因子时,称此类KS-代数为Kadison-singer因子,简称KS因子.若B(H)中的投影格L是生Von Neumann代数L″的最小自反格,即L自反且A lg(L)是KS-代数,则称L为KS-格.
In表示n阶矩阵单位,在不引起混淆时,简记为I.另外,引入矩阵代数Mn(C)中的矩阵单位系统Ei,j,i,j=1,2,…,n,其中 Ei,j表示第 i行第 j列为 1,其他位置为 0 的 n 阶方阵.由于讨论的为四阶矩阵,因此,这里n=4.
引理1 设L是B(H)的一个有限投影格,则L为完全分配格等价于∀E∈L,E#=E[6].
引理2 设V是无限域上的有限维向量空间,L是V的子空间格的有限格,那么,L是自反的当且仅当L 是分配格[7,8].

接下来的部分就是利用这两个例题中出现的KS-格,嵌入到四阶矩阵代数中得到的新的KS-格.
2 四阶矩阵代数中两个新的kadison-singer格的例子
命题1 设 P1=E11,+E33,P3=P1∨ P2=,则 L= {0,P1,P2,P3,I}为生成Von Neumann代数M2(C)⊕C⊕C的KS-格.
证明 首先,由于P1∧P2=0,P1∨P2=P3,所以易证L为一个格.进一步验证,L是一个分配格.经简单计算,对任意E,F,G∈L,均有(E∨F)∧G=(E∧G)∨(F∧G).因此,L是一个自反格.
设 A=(aij)∈A lg(L),aij∈C ,根据 P1AP1=AP1,可得 a21=0,a31=0,a41=0;根据 P2AP2=AP2,可得a11+a12=a22,a13=a23,a42=0,a43=0.所以,

从而有L'=(A lg L)∧(A lg L)*=C I2⊕C⊕C,可得L″=M2(C)⊕C⊕C.
下面证明L的极小性.
去掉 P1,则 M0={0,P2,P3,I}⊆L,M0的格代数为

进一步得到L″=C I2⊕C⊕C,即L不能生成von neumann代数M2(C)⊕C⊕C,所以P1不能去掉.
去掉P2,则L中余下的元素组成的集合M0= {0,P1,P3,I},P1,P3同上.显然,M0中的元素是可交换的,因此,M0生成的von neumann代数是可交换的,与M2(C)⊕C⊕C的不可交换性矛盾.所以,P2不能去掉.极小性得证.

从而可得:L″=M3(C)⊕C.
下面证明L的极小性.
去掉 P1,则 L= { 0,P2,P3,P4,I}.由于P1=P2∧P4,此时,P2∧P4∉L,由格的定义可知,L不是一个格,所以L更不可能为一个KS-格.

可得L'=(A lg L)∧(A lg L)*=C⊕C I2⊕C,所以L″=C⊕M2(C)⊕C≠M3(C)⊕C,因此,P3不能去掉.
由于P4=P1∨P3,当P1,P3∈L时,保证L为一个格,P4必须∈L.
由以上所述可知,L={0,P1,P2,P3,P4,I}为生成Von Neumann代数M3(C)⊕C的KS-格.
利用低阶矩阵代数中已经研究的比较彻底的KS-格嵌入到高阶矩阵中,进而构造出高阶矩阵代数中一些新的KS-格的方法,可以作为一种构造KS-格的方法在研究KS-格时使用.
[1]KADISON R.SINGER I.Triangular operator algebras.Fundamentals and hyper-reducible theory[J].Amer Journal of math,1960(82):227-259
[2]GE L,YUAN W.Kadison-Singer algebras,Ι[J].hyperfinite case,Proc.Natl.Acad.Sci.USA,2010,107(5):1838-1843
[3]GE L,YUAN W.Kadison-Singer algebras,Ⅱ[J].hyperfinite case,Proc.Natl.Acad.Sci.USA,2010,107(11):4840-4844
[4]HOU G J.Cohomology of a class of Kadison-Singer algebras.Science in China Series A[J].Mathematics,2010,53:1827-1839
[5]董璦菊,侯成军,谭军.矩阵代数Kadison-Singer格的分类[J].数学学报:中文版,2011,54(2):333-342
[6]鲁世杰,陆芳言,李鹏同,等.非自伴算子代数[M].北京:科学出版社,2004
[7]胡长流,宋振明.格论基础[M].开封:河南大学出版社,1990
[8]周惊雷.分配格上向量线性相关性探讨[J].重庆工商大学学报:自然科学版,2010,27(4);319-321

