无可微性和凸性包含问题的误差界*

徐 述

(重庆警察学院 后勤处，重庆401331)

研究下列包含问题:

其中f:X→Z是一个向量值映射，X和Z是两个巴拿赫空间且其范数都统一用符号‖·‖表示，K是Z中的一个非空闭集.令S={x:f(x)∈K}且在文中总是假设S≠∅.如果存在 的某个邻域U和常数α＞0，使得式(2)成立:

当K={0}时，包含问题(1)退化为一个等式.对该等式问题的各种误差界在可微性的条件下已经被很多学者研究，如 Graves［1］，Izmailov 和 Solodov［2］及 Lyusternik［3］.当 K=和 Z=Rm且 m≥1 时，包含问题(1)变为有限不等式组.对该不等式组的误差界在函数可微或不可微的情况都有讨论［4-12］.当K是一个非空闭凸锥时，Robinson［13］在一种约束品性和可微性条件下证明了式(2)是成立的.最近，利用其他的条件和方法，He和Sun［14］讨论了不用于式(2)的两类误差界.当K是一个非空闭凸集时，Burke和Deng［15］在可微和凸性条件下证明了式(2)是成立的.此外，对非光滑包含问题的误差界，许多学者如He和Sun［16］，Huang和Ng［17］，Ng和 Yang［18］，Ng 和 Zheng［19-20］，Wu 和 Ye［21-23］及 Zheng［24］等人都做了一些重要工作.

此处主要讨论包含问题(1)形如(2)的误差界，此时函数f不需要可微性和凸性条件，且K仅仅是一个非空闭集.文章将在第2部分介绍一些重要的概念和引理;在第3部分建立不需要可微性和凸性条件的局部误差界和全局误差界.

1 预备知识

设h:X→Z是一个向量值映射.

定义1 给定点(x^，z^)∈gph F，如果存在常数k≥0，x^的邻域U和z^的邻域W，使得

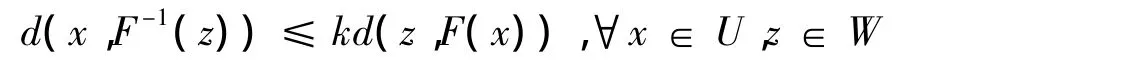
成立，则称F在点(x^，z^)是度量正则的.称满足上述不等式的所有(k，U，W)中的k的下确界为F在点(x^，z^)的精确度量正则常数且记为reg F(x^，z^).

如果存在常数k≥0使得下式(3)成立

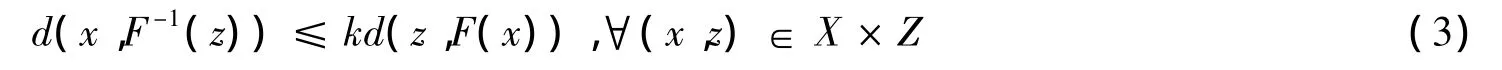
则称F在X×Z上是度量正则的.

类似地，可以定义单值函数h:X→Z的度量正则且相应的常数记为reg h(x^).

下面回顾一个重要的引理.此引理是命题1［25］的一个特殊形式.S

引理1 设 ∈ 且f在点 是连续的，则S在点 具有局部Lipschitz误差界，即式(2)成立，当且仅当存在 的邻域U和常数c＞0，使得式(4)成立

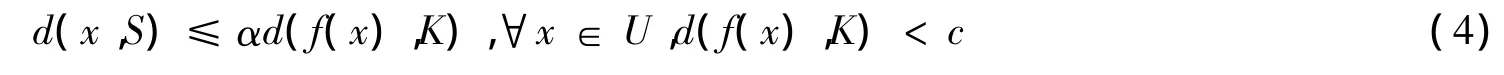
2 无可微性和凸性的包含问题的误差界

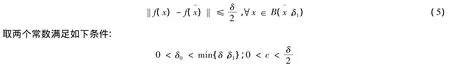
对任意的x∈B( ，δ0)且 d(f(x)，K)＜c，如果 d(f(x)，K)=0，则根据 K 的闭知 x∈S，从而不需要证明.下面考虑情形d(f(x)，K)＞0.对任意的ε满足0＜ε＜c－d(f(x)，K)，则存在zε∈K 使得‖f(x)－zε‖≤d(f(x)，K)+ε.因为

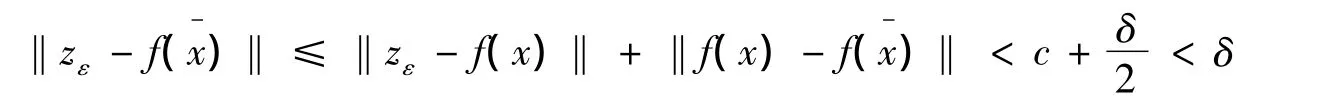
则结合(i)得 d(x，f－1(zε))≤a‖zε－f(x)‖.所以存在 xε∈f－1(zε)(即 zε=f(xε))使‖x － xε‖≤a‖zε－ f(x)‖ +ε.而且有 xε∈S.因此得

因为ε可以任意逼近0，所以包含问题(1)具有局部Lipschitz误差界，相关的精确误差界常数的上界容易得到.证毕.

注1 下面这个例子说明了f的度量正则性质对定理1是本质的.令X=Z=R，f(x)=x2和K={0}∪=0［1，∞)，则有 S={0}∪(－∞，－1］∪［1，∞).令 ，容易验证f在 点不是度量正则的.且明显地，包含问题(1)不具有局部Lipschitz误差界.

证明 令 x∈X，如果 d(f(x)，K)=0，则根据 K的闭性得 x∈S，从而不需要证明.下面考虑情形:d(f(x)，K)＞0.因为K非空，所以对任意的ε＞0都存在zε∈K，使得

因为ε可以任意逼近0，包含问题(1)具有全局Lipschitz误差界.证毕.

下面回顾度量正则的一个充分条件.

引理 2［26］令∈S，给定一个满射线性连续算子A:X→Z，假设存在的某个邻域U，常数μ≥0和γ＞reg A满足

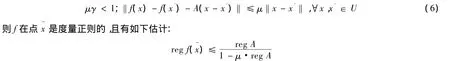
注2 f的度量正则性质一般不蕴含公式(6).类似地，下面这个条件是f在X上的度量正则的充分条件:存在一个满射线性连续算子A:X→Z，常数μ≥0和γ＞reg A满足μγ＜1及

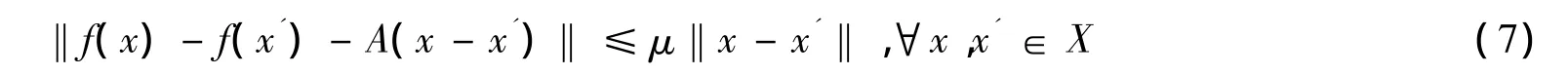
根据定理1，2和引理1及注2很容易得到下面的结论.

注3 (i)条件(6)的一个充分条件是严格可微性，容易从如下定义中看出.f在点 是严格可微的且严格导数记为∇f()当且仅当，∀x，x'∈X 且在的某个邻域内.

但是条件(6)一般不蕴含f的Gateaux可微性，Gateaux可微性是比严格可微性更弱的一个条件.所以条件(6)一般不蕴含严格可微性，更不蕴含度量正则性质.令X=Z=R，0和f(x)=|x|，容易验证条件(6)对和μ=2成立.明显地，f在点不是Gateaux可微的.因此，此处的条件和方法不同于文献［13，15］中的条件和方法.

(ii)在f关于K的回收锥K∞是凸的条件下，Burke和Deng［5］已经研究了包含问题(1)的Lipschitz误差界(2)，其中凸性假设和回收锥K∞是:

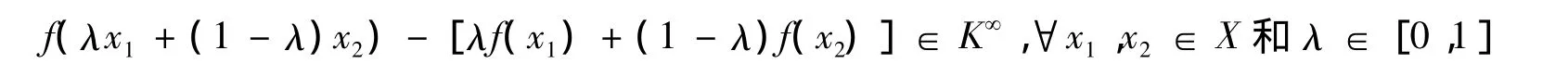
K∞:={d:x+d∈K∀x∈K}.容易验证条件(4)一般不蕴含f的凸性.所以此处的结论和方法不同于Burke和Deng［5］.

(iii)定理1，2和推论1可以应用到下列向量优化问题(简记为:VOP):

其中f:X→Z是一个向量值映射且C⊂Z是一个带有非空内部int C的凸锥，用M表示可性值，即，M:={f(x):x∈X}.令K1和 K2分别是

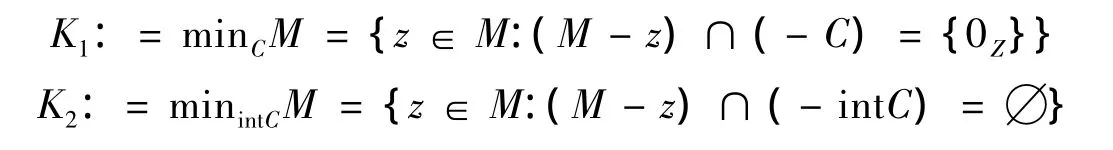
即K1和K2分别是(VOP)的最优值和弱最优值集合.用S1和S2分别表示(VOP)的有效解和弱有效解，则

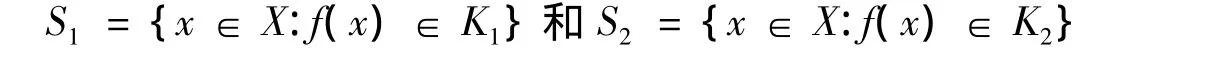
因此定理1，2和推论1可以应用到(VOP)的有效解和弱有效解集.但是，由于集合K1和K2一般既不是凸集也不是锥，所以文献［13－16，18，24］的结论一般不能应用到(VOP)上.

［1］GRAVESL M.Some mapping theorems［J］.Duke Math J，1950(17):111-114

［2］IZMAILOV A F，SOLODOV M V.Error bounds for 2-regular mappings with Lipschitzian derivatives and their applications［J］.Math Program Ser A，2001，89(3):413-435

［3］LYUSTERNIK L A.On conditional extrema of functionals［J］.Mat Sbornik，1934(41):390-401

［4］AUSLENDER A，TEBOULLE M.Asymptotic Cones and Functions in Optimization and Variational Inequalities［M］.New York:Springer，2003

［5］BURKE JV，DENG S.Weak sharp minima revisited，part II:application to linear regularity and error bounds［J］.Math Program Ser B，2005(104):235-261

［6］KLATTE D，LI W.Asymptotic constraint qualifications and global error bounds for convex inequalities［J］.Math Program Ser A，1999，84(1):137-160

［7］LEWISA S，Pang J-S.Error bounds for convex inequality systems［A］.In:Crouzeix，J.P.，Martinez-Legaz，J.-E.，Volle，M.(ed.)Proceedings of the Fifth International Symposium on Generalized Convexity held in Luminy June［C］.Kluwer Academic Publishers，Dordrecht，1998

［8］Li W.Abadie’s constraint qualification，metric regularity and error bounds for differentiable convex inequalities［J］.SIAM J.Optim，1997，7(4):966-978

［9］MANGASARIAN O L.Error bounds for nondifferentiable convex inequalities under a strong Slater constraint qualification［J］.Math.Program，1998(83):187-194

［10］NGAI H V，THERA M.Error bounds for convex differentiable inequality systems in Banach spaces［J］.Math.Program.Ser.B，2005(104):465-482.

［11］PANG JS.Error bounds in mathematical programming［J］.Math Program Ser B，1997(79):299-332

［12］ROBINSONSM.An application of error bounds for convex programming in a linear space［J］.SIAM JControl，1975(13):271-273

［13］ROBINSON SM.Stability theory for systems of inequalities.II.Differentiable nonlinear systems［J］.SIAM J Numer Anal，1976，13(4):497-513

［14］HE Y R，SUN J.Error bounds for degenerate cone inclusion problems［J］.Math Oper Res，2005，30(3):701-717

［15］BURKE J V，DENG S.Weak sharp minima revisited，Part III:error bounds for differentiable convex inclusions［J］.Math Program Ser B，2009(116):37-56

［16］HE Y R，SUN J.Second order sufficient conditions for error bounds in Banach spaces［J］.SIAM J Optim，2006，17(3):795-805.

［17］HUANG L R，NG K F.On first and second-order conditions for error bounds［J］.SIAM JOptim，2004，14(4):1057-1073

［18］NG K F，YANG W H.Error bounds for abstract linear inequality systems［J］.SIAM JOptim，2002，13(1):24-43

［19］NG K F，Zheng X Y.Global error bounds with fractional exponents［J］.Math Program Ser B，2000，88(2):357-370

［20］NGK F，Zheng X Y.Error bounds for lower semicontinuous functions in normed spaces［J］.SIAM JOptim，2001，12(1):1-17

［21］WU Z L，YE J J.Sufficient conditions for error bounds［J］.SIAM J Optim，2001，12(2):421-435

［22］WU Z L，YE J J.On error bounds for lower semicontinuous functions［J］.Math Program Ser A，2002，92(2):301-314

［23］WU Z L，YE J J.First-order and second-order conditions for error bounds［J］.SIAM J Optim，2003，14(3):621-645

［24］ZHENGX Y，NGK F.Error bound moduli for conic convex systems on Banach spaces［J］.Math Oper Res，2004，29(2):213-228

［25］LI M H，LI SJ.Robinson metric regularity of parametric variational systems［J］.Nonlinear Anal，2011(380):354-362

［26］ARTACHO F JA，MORDUKHOVICH B S.Enhanced metric regularity and Lipschitzian properties of variational systems［J］.J Global Optim，2011(50):145-167