观察法判断一元函数的一致连续性

刘 倩，任晓花

(重庆师范大学数学学院，重庆401331)

1 引言及基本概念

“函数的一致连续性”是数学分析的一个重点和难点，一致连续性刻画了函数在某个区间的整体性质，是微积分学的基础.目前判定和证明函数一致连续性的方法很多［1-3］，但是判断和证明的过程比较繁琐，此处将引进一种新的判断函数一致连续性的方法——观察法.通过对连续模数的学习，认真总结，结合MATLAB，并运用实例证明这种方法非常的快速有效.下面介绍所涉及的基本概念.

定义 1［4］设 f为定义在区间 I上的函数，若对任给的 ε ＞0，存在 δ= δ(ε)＞0，使得对任何 x'，x″∈I，只要就有，则称函数f在区间I上一致连续.

注1 f在I上一致连续意味着:不管两点x'，x″在区间I中处于什么位置，只要它们的距离小于δ，就可使

定义 2［5］若f(x)在区间I上有定义，则ω(δ)=称为函数f的连续模数，ω(δ)ff是关于δ的非负、不减函数.

2 主要结论及其证明

定理1 若f(x)在区间I上有定义，则f(x)在I上一致连续的充要条件是(δ)=0.

证明 (1)必要性.因 f(x)在 I上一致连续，因此∀ε＞0，∃δ1＞0，当时，有，从而

所以f在I上一致连续.证毕.

因为ωf(δ)的值只与f的图形最陡的地方有关，根据定理1可得一元函数一致连续性的观察法.

下面借助于 MATLAB［6］作出 f(x)＞0)的图像，利用定理2，描述出函数的一致连续区间.并证明其正确性.

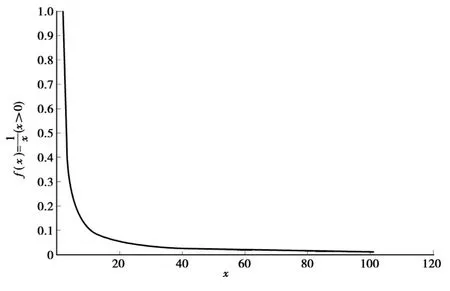
图1 函数一致连续区间

由图像可以看出，在x=0处，图形无限变陡，∀δ＞0，ωf(δ)=+∞(δ)≠0.因此 f在任何区间(0，c)(c＞0)上都是非一致连续的，但在区间［c，+∞］上，f(x在点c处最陡，且ω(δ)(δ→0+)，可见 f(x)在［c，+∞］上一致连续.

3 结束语

一致连续性表示在区间的任何部分只要变元的两个数值达到一定的接近程度，就可以使对应的函数值达到所需要的接近程度.因此可以看出函数的一致连续性与定义区间的紧性有很大的关系.此处从函数图像的角度，对函数一致连续性作了简单的讨论.但这种方法也有不足之处，对于函数图像复杂的，或不知道函数图像的并不适用.一致连续性是数学分析的一个难点，在物理、工程方面的应用也很广泛，希望以后做更深入的研究.

［1］韩仲平.函数的一致连续性分析［J］.内江科技，2009(5):72-73

［2］姜雄.关于函数在任意区间上一致连续性与非一致连续性的条件的讨论［J］.辽宁科技学院报，2005(7):35-36

［3］马砦伟，杜炜，朱娴.关于函数的一致连续性的一点注记［J］.科技资讯，2009(2):253

［4］华东师范大学数学系.数学分析［M］.3版.北京:高等教育出版社，2004

［5］裴礼文.数学分析中的典型问题与方法［M］.2版.北京:高等教育出版社，2006

［6］萧树铁.数学实验［M］.2版.北京:高等教育出版社，2008