Application of signal sparse decomposition in dynamic test*
XUAN Zhi-wei(轩志伟), XUAN Chun-qing(轩春青), CHEN Bao-li(陈保立)
(1. College of Information and Communication Engineering, North University of China, Taiyuan 030051, China;2. Department of Information Engineering, Zhengzhou Chenggong University of Finance and Economics, Zhengzhou 451200, China)
Application of signal sparse decomposition in dynamic test*
XUAN Zhi-wei(轩志伟)1, XUAN Chun-qing(轩春青)2, CHEN Bao-li(陈保立)1
(1. College of Information and Communication Engineering, North University of China, Taiyuan 030051, China;2. Department of Information Engineering, Zhengzhou Chenggong University of Finance and Economics, Zhengzhou 451200, China)
In dynamic test, sampling rate is high and noise is strong, so a signal sparse decomposition method based on Gabor dictionary is put forward. This method iteratively decomposes the signal with the matching pursuit (MP) algorithm and takes the coherence ratio of the threshold as a condition of iteration termination. Standard MP algorithm is time-consuming, thus an adaptive genetic algorithm is introduced to MP method, which makes computation speed accelerate effectively. Experimental results indicate that this method not only can effectively remove high-frequency noise but also can compress the signal greatly.
dynamic test; sparse decomposition; matching pursuit (MP) algorithm; denoising; compression
0 Introduction
With the development of the scientific research, more and more transient signals need to be measured accurately. High sampling rate is required when the signals change fast, so there will be an enormous amount of data generated by measuring. In the process of measuring, the electronic equipments will bring high-frequency noise into measurement results, so compression and denoising are significant methods for signal processing in dynamic test[1].
From Fourier transform to wavelet analysis, signal analysis and processing methods have been greatly improved, but there are still a lot of shortcomings. Because the basis set is thinning in signal space and the signal can not be sparse when it is decomposed in this basis set. While in the over-complete dictionary of atoms, the basis sets are dense enough in signal space and any signal can be expressed by a set of best matching atoms. Therefore the signal becomes sparser when it is decomposed in the over-complete dictionary of atoms[2].
In 1993, sparse decomposition method was put forward firstly. After that it quickly became a new tool in signal processing. Now it has been successfully used in signal denoising, parameter estimation, compression perception, etc.
In this paper, a signal sparse decomposition method is put forward based on matching pursuit (MP) algorithm. It decomposes the dynamic test signals with the Gabor dictionary and achieves denoising and signal compression[3].
1 Algorithm realization
1.1 Matching pursuit algorithm
The MP algorithm is adopted to choose the best atoms in sparse decomposition, which is a kind of greedy iteration algorithm. Sparse decomposition of a signal can be obtained by iteratively projecting a signal onto a given over-complete dictionary and choosing the dictionary atom that best matches the signal for each iteration. Its fundamental principle can be described as follows:
Let H be a Hilbert space and D={gr∂m, m=0,1,…,M-1} be the over-complete dictionary in H. The atoms are normalized, satisfying ‖gr∂m‖=1. Let x(t) be the signal and it can be decomposed as
(1)

1.2 Over-complete dictionary
The construction of the over-complete dictionary is a very important step for signal sparse decomposition. Firstly, the dictionary must be over-complete, and then a group of atoms can be found to express any signal. The characteristics of atoms must be suit for the signals. Since dynamic test signals are non-stationary, the atoms must have time-frequency characteristic.
Gabor dictionary is an over-complete dictionary which is the most popular in application. The Gabor atoms can be expressed as
(2)
γ=(2j,p2j,kπ21-j,iπ/6), j,p,k,i∈z,
(3)
and then the atoms can be expressed as
gγd(n)=gj(n-2j·p)cos(nkπ·21-j+iπ/6),

(4)
where N is the length of the signal, L=log2(N), j∈(0,L], p∈[0,2-jN], k∈[0,2j) and i∈[0,11].
1.3 Adaptive genetic algorithm
MP algorithm is easy to be understood, but its calculation is time-consuming. Especially when the signal length and the number of atoms are huge, the calculation price is difficult to be accepted in actual application. Genetic algorithm is a kind of global parallel search algorithm with high efficiency, which can reduce computing times. However, the standard genetic algorithm also has many shortcomings. In this paper, an improved adaptive genetic algorithm is put forward.
There are two major parameters in genetic algorithm, namely crossover Pcand the mutation probability Pm. They influence the convergence speed directly. Pcdetermines the creation speed of new individual. Higher crossover may destroy the mode of the excellent individual and lower crossover will delay the production of new individual which may lead to premature convergence. Pmdetermines the ability jumping out of the local optimal solution. If mutation probability is lower, the generation speed of new model will be slow. While mutation probability is higher, the algorithm will become random search algorithm to some extent. The ideal situation is that Pcand Pmare assigned adaptively according to the sort order of fitness in the population.
Rinvivas M S put forward an adaptive genetic algorithm, but the search ability of his algorithm was relatively weak in the early evolution[5]. Therefore, an improved adaptive genetic algorithm is put forward in this paper. Pcand Pmare calculated by
(5)
(6)
where fmaxis the maximal fitness in population, favgis the minimal fitness in population, f′ is the bigger fitness of the two individuals need to cross and f is the fitness of the individual needs to be mutated. In this paper, Pc1equals 0.9 and Pc2equals 0.6; Pm1equals 0.1 and Pm2equals 0.001.
1.4 Iteration termination condition
The quality of reconstruction signals is influence by the iteration times of MP algorithm, finding reasonable times of the iteration is very important to improve the performance of MP algorithm. The traditional iteration termination conditions mainly include two kinds as follows:
1) Fixed iteration times. Set a value m, the loop iteration stops when the number of iteration equals m. The bigger m may bring much noise in reconstruction signals, while the smaller m may result in loss of information.
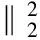
In application, the dynamic test signals consist of useful information and noise. There is strong coherence between useful information and atoms, while there is little coherence between noise and atoms beacuse the noise is always Gaussian random noise. With the increase of iteration times, useful information is extracted step by step and the coierence between residual signal and atoms gradually decreases. Thus the coherence ratio is taken as the termination condition of iteration[7]. Coherence ratio is defined as
(7)
After the threshold of the residual coherent ratio is assigned, the iteration times will change adaptively as signal SNR level. In this way, extracting useful information in maximum and noise in minimum can keep balance.
2 Experimental tests
In order to verify the practical performance of the method proposed in this paper, we designed a memory-type temperature measuring system and got a group of data by it. The curve of temperature signal to be tested is drawn in Fig.1.

Fig.1 Tested signal
From Fig.1, it can be seen that the tested data contain a lot of unavoidable noise. The noise limits that the data can be used for in a certain extent. The experiment includes a 12-bit A/D chip and each sampling result takes 2 byte and the sample rate is 1 MHz. Every time we need 1 s to get the data, so the final date is about 2 Mbyte. If the sample rate is higher, the data will take more space.
The temperature signal shown in Fig.1 is decomposed with the method described in this paper. The default setting of the population size is 21, the evolution time is 100 in genetic algorithm and the threshold of coherence ratio is set to 0.005. The rest of the parameters are selected according to explanations in section 1.3.
The reconstruction signal is shown in Fig.2 and the residual signal is shown in Fig.3. Obviously, the reconstruction signal is very smooth while the residual signal is almost high-frequency white noise.
The Fig.4 shows the change of the coherence ratio. It can be seen that coherence ratio reduces with the increase of iteration times. The coherence ratio rises and falls at first, but at last it is overall reduced. So setting a threshold of coherent ratio as termination condition is feasible. In this experiment, coherence ratio threshold is set to 0.005. After 14 times iteration, the coherence ratio equals 0.004 2, being lower than the threshold. Thus the iteration calculation is completed.

Fig.2 Reconstructed signal

Fig.3 Residual signal

Fig.4 Changing curve of coherence ratio
In order to verify the performance, a comparison is made between the improved method and standard MP method. The same signal is decomposed and reconstructed using different ways in Matlab on the same computer. The computer has a 2.00 GHz Intel Pentium dual E2180 CPU, 1.00 GB RAM, and windows XP operating system. The consumed time is shown in Table1.

Table 1 Comparison of two methods
From the experimental results, it can be seen that the improved method can reduce noise and compress the signals at the same time. Since the choice of dictionaries is not limited, the sparse decomposition provides extremely flexible signal representations. For example, the temperature signal is expressed as a linear combination of 14 total atoms and each atom only has 5 parameters. Hence only 70 parameters can represent the original temperature signal which size is 1.326 Mbyte.
3 Conclusions
1) The sparse decomposition method provides extremely flexible signal representation. The method described in this article not only removes the noise well but also dramatically compress the size of the signals.
2) The adaptive genetic algorithm and the coherence ratio threshold termination rule improve the efficiency and intelligence of MP algorithm although there still is chance to enhance the speed of computing. Actually the tested signals are usually band-limited signals, If we know the frequency ranges of the tested signals in advance, we can reduce the number of atoms of the dictionary and then increase the speed of computing.
[1] LIU Xu, XIA Jin-dong, WU Miao. Study on wavelet denoise and characteristic extraction of echo signal to flaw classification in ultrasonic testing. Journal of China University of Mining and Technology, 2001, 30(3): 248-251.
[2] JIA Qing-quan, YU Lian-fu, WANG Ning, et al. Application of atomic sparse decomposition to power systems disturbance analysis. Power System Protection and Control, 2010, 38(19): 17-21.
[3] ZHANG Chun-mei, YIN Zhong-ke, XIAO Ming-xia. Signal representation and sparse decomposition based on overcomplete dictionary. Chinese Science Bulletin, 2006, 51(6): 628-633.
[4] Mallat S, Zhang Z. Matching pursuits with time-frequency dictionaries. IEEE Transaction on Signal Processing, 1993, 41(12): 3397-3415.
[5] WANG Xiao-ping, CAO Li-ming. The genetic algorithm, theory, applied and the software realization. Xi'an: Xi'an Jiaotong University Press, 2002.
[6] LIANG Wei, XUE Pei-wen, CHEN Liang, et al. Residual ratio iteration termination condition for MP method. Journal of Shanghai Jiaotong University, 2010, 44(2): 171-175.
[7] WANG Jian-ying, YIN Zhong-ke, ZHANG Chun-mei. Signal and image sparse decomposition and preliminar application. Chengdu: Southwest Jiaotong University Press, 2006: 94-100.
[8] CHEN Bao-li, CHEN Yu, ZHANG Fei-yue, et al. Ultrasonic nondestructive signals processing based on sparse decomposition. Application of Electronic Technique, 2012, 38(8): 140-142.
date: 2013-01-09
XUAN Zhi-wei(shine071201@163.com)
CLD number: TN911.72 Document code: A
1674-8042(2013)03-0243-04
10.3969/j.issn.1674-8042.2013.03.009
 Journal of Measurement Science and Instrumentation2013年3期
Journal of Measurement Science and Instrumentation2013年3期
- Journal of Measurement Science and Instrumentation的其它文章
- Test on oxygen and benzene contents in gasoline by mid-infrared spectroscopy*
- Particle-filter-based walking prediction model for occlusion situations*
- Automatic estimation and removal of noise on digital image*
- Kravchenko probability weight functions in problems of radar signals correlation processing*
- AC current automatic calibration using two different TCC designs*
- Smart decontamination device for small-size radioactive scrap metal: using abrasion pin in rotating magnetic field and ultrasonic wave cleaner*
