Kravchenko probability weight functions in problems of radar signals correlation processing*
V F Kravchenko, D V Churikov
(Kotel’nikov Institute of Radio Engineering and Electronics of Russian Academy of Sciences, Moscow 125009, Russia)
Kravchenko probability weight functions in problems of radar signals correlation processing*
V F Kravchenko, D V Churikov
(Kotel’nikov Institute of Radio Engineering and Electronics of Russian Academy of Sciences, Moscow 125009, Russia)
In this report the combined method of correlation radar signal (RS) processing based on the theory of atomic functions (AF) is examined. Examples of using of new Kravchenko probability weight functions (WF) designs are presented. Quality functional to estimate accuracy and efficiency of RS processing for concrete physical models is constructed. It is shown that the proposed approach significantly improves the quality of the coherent analysis of RS.
radar signal (RS); atomic funtions (AF); weight functions (WF)
0 Introduction
In radar systems[1-3], the pair of coherent reference and input signals are used for optimal signal processing. Such device of coherent filtering (CF) performs the following operation:

(1)
where Sx(t) and S0(t) are the complex envelopes of the input and the reference signals, τ is delay time signal relative to the moment of sensing and p is Doppler frequency shift. If the frequencies of the received and reference signals are matched then

(2)
1 Formulation of the problem and solution method
Most noise protection radar devices can be achieved using sophisticated sounding signals[1-7]. In addition it reduces the power consumption of the equipment compared with the use of frequency-modulated pulses. However in CF interference effects arise and distort the processing results. This phenomenon can be eliminated by the introduction to the correlation integral of weight functions (WF) or WA-system functions[7-22]w(t) in the following form:
|Yw(τ,p)|=
(3)
The following classis of weight functions on the basis of probability atomic functions (AF)[2-16]are taken:
Kravchenko-Cauchy
(4)
Kravchenko-Laplace
(5)
Logistic-Kravchenko distribution
(6)
Kravchenko-Champernoune
(7)
In Eqs.(4)-(7) , g, b, λ and α are scale parameters. Their plots and spectra are presented in Figs.1-4.

Fig.1 Plot of w1(t) and its spectra
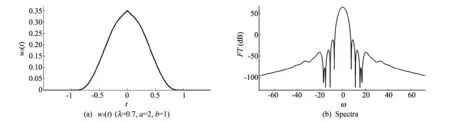
Fig.2 Plot of w2(t) and its spectra

Fig.3 Plot of w3(t) and its spectra

Fig.4 Plot of w4(t) and its spectra
Block diagram of Doppler frequency calculation algorithm with the improvement is shown in Fig.5. There is correlation processing of the input and reference signals. Further defined frequency channels with the maximum value of the signal the next one. Complex envelope passes through the filter system. At the final stage the value of the Doppler shift (relative to the reference signal) is calculated by
(8)
where pmaxis the position of the autocorrelation function maximum and pimis improving value

(9)

Fig.5 Block diagram of Doppler frequency estimation
WF reduces the side lobe level (SLL) located near the main peak to improve resolution of the peaks at superposition of two signals. The limitation is the broadening of the main lobe. For Rayleigh criterion, this leads to an increase in the minimum frequency shift (Doppler frequency), which can be determined.
The 4th order Hermite polynomial is selected as a test signal. Its plot and ambiguity function are presented in Fig.6. Fig.7(a) shows the results of the coherent filtering of signal with a phase shift without the weight processing that can improve radar signal (RS) correlation processing (Fig.7(b)).

Fig.6 Plot of 4th order Hermite polynomial and its ambiguity function

Fig.7 Coherent filtering of radar signal with a phase shift
2 Quality functional of coherent radar signal processing
To assess the quality of processing of RS, the following physical parameters are used: the relative broadening of the main lobe at level of -3 dB (Δ3,%), the maximum level of side lobes (γ1), side lobe with a maximum level (γ2), the relative decrease in the level of the first side lobe (γ3). Doppler frequency is determined by the proposed algorithm (Fig.1). Quality functional has the form
100(γ2-0.69)-3γ3).
(10)
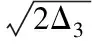
Table 1 Values of physical parameters and the quality functional of the CRSP for weighting function w1(t) (b=a)

agΔ3(%)γ1γ2γ3J20.627.650-9.3100.7021.2601.28720.722.923-9.6090.7020.9601.27120.819.628-9.8520.6990.7781.29520.917.192-10.0540.6990.6551.2362115.330-10.2200.6960.5681.25330.623.209-9.6090.6990.9821.34030.718.911-9.9210.6960.7351.35630.815.903-10.1740.6960.5811.28130.913.610-10.3830.6930.4751.2773111.891-10.5540.6930.3991.20740.620.917-9.9150.6990.9001.23940.716.762-10.2510.6960.6651.23640.813.754-10.5270.6930.5161.21840.911.605-10.7530.6930.4141.13150.620.201-10.0070.6990.8821.20050.716.046-10.3620.6990.6511.11350.813.037-10.6500.6960.5021.08850.910.888-10.8900.6930.4011068
Table 2 Values of physical parameters and the quality functional of the CRSP for weighting function w2(t) (b=a)

agΔ3(%)γ1γ2γ3J20.411.175-10.6850.6930.4141.12520.512.464-10.5400.6960.4801.10320.614.040-10.3950.6960.5511.16320.715.473-10.2540.6960.6281.20620.817.049-10.1160.6960.7111.24830.610.458-10.7430.6930.3811.09730.711.891-10.5970.6930.4451.16130.813.324-10.4530.6930.5151.21640.811.318-10.8330.6900.4491.14450.810.458-10.9740.6930.4331.000
Table 3 Values of physical parameters and quality functional of CRSP for weighting function w2(t) (b=a-1)

agΔ3(%)γ1γ2γ3J30.433.524-8.5660.7020.9621.88430.535.244-8.4840.7021.0511.89030.636.963-8.4040.7021.1481.88730.738.825-8.3250.7051.2531.80730.840.688-8.2460.7051.3681.79340.420.774-9.4070.6960.5671.68540.522.350-9.3050.6960.6361.71840.623.926-9.2030.6990.7111.67140.725.501-9.1020.6990.7921.69140.827.077-9.0030.6990.8801.70450.414.183-9.9310.6900.3601.57950.515.616-9.8210.6900.4221.62650.617.049-9.7090.6930.4871.59250.718.481-9.6000.6930.5571.62750.819.914-9.4930.6930.6311.657
Table 4 Values of physical parameters and quality functional of CRSP for weighting function w3(t) (b=a)
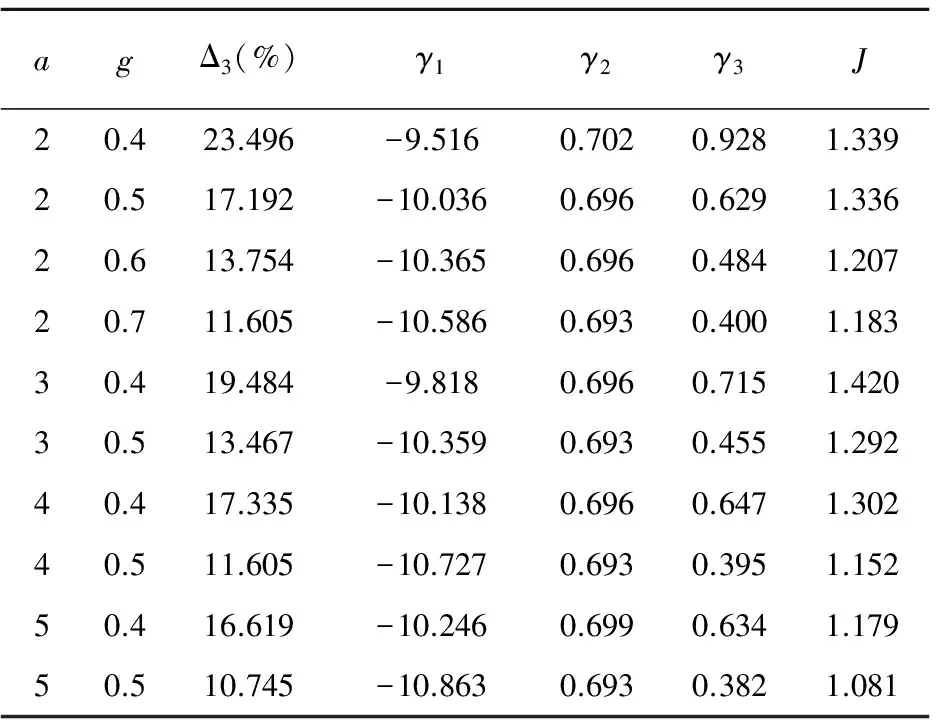
agΔ3(%)γ1γ2γ3J20.423.496-9.5160.7020.9281.33920.517.192-10.0360.6960.6291.33620.613.754-10.3650.6960.4841.20720.711.605-10.5860.6930.4001.18330.419.484-9.8180.6960.7151.42030.513.467-10.3590.6930.4551.29240.417.335-10.1380.6960.6471.30240.511.605-10.7270.6930.3951.15250.416.619-10.2460.6990.6341.17950.510.745-10.8630.6930.3821.081
Table 5 Values of physical parameters and quality functional of CRSP for weighting function w3(t) (b=a-1)

agΔ3(%)γ1γ2γ3J30.539.685-8.2230.7051.1461.93730.635.817-8.4040.7020.9901.97230.733.524-8.5230.7020.8991.94230.831.948-8.6060.7020.8421.91540.433.095-8.5930.7021.0421.80440.526.648-8.9570.6990.7581.79240.623.209-9.1890.6990.6171.71840.721.060-9.3430.6960.5361.73440.819.771-9.4480.6960.4861.69650.425.788-9.0270.6960.8091.78250.519.771-9.4320.6930.5471.72950.616.476-9.6860.6930.4191.62450.714.613-9.8550.6900.3431.63050.813.324-9.9700.6900.2961.576
Table 6 Values of physical parameters and quality functional of CRSP for weighting function w4(t) (b=a)
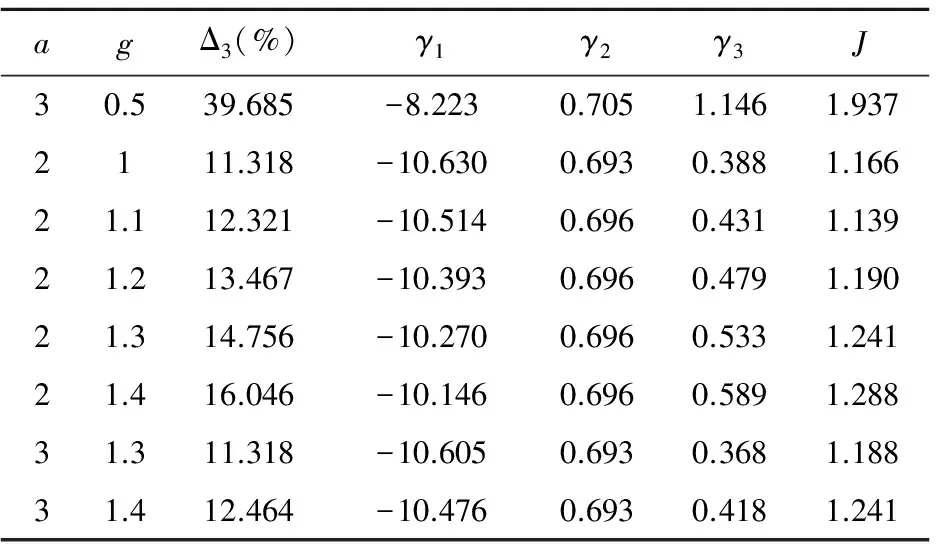
agΔ3(%)γ1γ2γ3J30.539.685-8.2230.7051.1461.9372111.318-10.6300.6930.3881.16621.112.321-10.5140.6960.4311.13921.213.467-10.3930.6960.4791.19021.314.756-10.2700.6960.5331.24121.416.046-10.1460.6960.5891.28831.311.318-10.6050.6930.3681.18831.412.464-10.4760.6930.4181.241
Table 7 Values of physical parameters and quality functional of CRSP for weighting function w4(t) (b=a-1)

agΔ3(%)γ1γ2γ3J3133.095-8.5470.7020.8871.93231.134.384-8.4830.7020.9351.95131.235.673-8.4190.7020.9901.96531.337.106-8.3510.7051.0471.90631.438.539-8.2820.7051.1101.9174120.774-9.3740.6960.5251.72441.121.777-9.2940.6960.5671.75141.223.066-9.2090.6990.6141.71041.324.212-9.1220.6990.6671.73441.425.645-9.0340.6990.7231.7655114.183-9.8890.6900.3321.61051.115.186-9.8010.6930.3721.57451.216.332-9.7080.6930.4161.61551.317.479-9.6130.6930.4621.65351.418.768-9.5180.6930.5131.693
3 Numerical experiment
Consider the following example to study the quality of the coherent processing of the RS (3).
Since the Hermite polynomial 4th order is selected as the reference signal, the input signal can be obtained as

Fig.8 Real and imaginary parts of input signal

(11)
The correction of time delay for the analysis of frequency changes is produced. The real and imaginary parts of the input signal are shown in Fig.8. The sections of the CF by plane with the weight processing can be seen in Fig.9.
Input signals with the weight processing and the results of the coherent filtering can be seen in Figs.10-11.
Physical characteristics and the value of quality functional of the coherent radar signal processing (CRSP) are presented in Tables 1-7.

Fig.9 Sections of CF without weight processing (τ=0 plane)

Fig.10 Real and imaginary parts of input signal with weight processing for w(t) (a=2, b=2, g=0.5)

Fig.11 Sections of the CF by plane x=0 with weight processing for w1(t) (a=2, b=2, g=0.5)
4 Conclusion
The new structure of the correlation filter with the use of combinations of WF on the basis of probability distributions Kravchenko is considered. By analysis of tables and graphs, it can be concluded that the proposed algorithm is reasonable and it has the flexibility and accuracy based on the use of Kravchenko weight functions.
Results of work were partially reported on IEEE 10th International Conference on Signal Processing Proceedings (ICSP’10)[20].
[1] Sloka V K. Problems of processing of radar signals. Sov. Radio, Moscow, 1970.
[2] Volosyuk V K, Kravchenko V F. Statistical theory of radio technical systems of remote sensing and radar. Fizmatlit, Moscow, 2008.
[3] Kravchenko V F, Labun’ko O S, Lerer A M, et al. Computing methods in the modern radio physics. Fizmatlit, Moscow, 2009.
[4] Kravchenko V F, Perez-Meana H M, Ponomaryov V I. Adaptive digital processing of multidimentional signals with applications. Fizmatlit, Moscow, 2009.
[5] Kravchenko V F. Lectures on the theory of atomic functions and their some applications. Radiotechnika, Moscow, 2003.
[6] Kravchenko V F, Rvachev V L. Boolean algebra, atomic functions and wavelets in physical applications. Fizmatlit, Moscow, 2006.
[7] Kravchenko V F. Digital signal and image processing in radio physical applications. Fizmatlit, Moscow, 2007.
[8] Gulyaev Y V, Kravchenko V F, Pustovoit V I. A new class WA-systems of Kravchenko-Rvachev functions. Doklady Mathematics, 2007, 75(2): 325-332.
[9] Gulyaev Y V, Kravchenko V F, Pustovoit V I. Kravchenko Kotel’nikov analytical wavelets in digital signal processing. Doklady Physics, 2007, 52(12): 645-652.
[10] Kravchenko V F, Meana H P, Ponomaryov V I., et al. Spectral estimation of digital signals by the orthogonal Kravchenko wavelets // Progress in pattern recognition, image analysis, computer vision, and applications. In: Proceedings of the 14th Iberoamerican Conference on Pattern Recognition (CIARP2009), Guadalajara, Jalisco, Mexico, 2009, 5856: 989-996.
[11] Kravchenko V F, Churikov D V. A new class of orthogonal kravchenko WA-system functions. Telecommunications and Radio Engineering, 2009, 68(8): 649-666.
[12] Kravchenko V F, Kravchenko O V, Safin A R. Atomic functions in probability theory and stochastic processes. Publishing House Successes of Modern Radio Electronics, 2009, 5: 23-39.
[13] Kravchenko V F, Kravchenko O V, Safin A R, et al. New class of probability weight functions in digital signal and image processing, An International Journal Electromagnetic Waves and Electronic Systems, 2009, 14(9): 31-44.
[14] Kravchenko V F. Atomic and R-functions in radiophysical applications. In: Proceedings of International Conference on Antenna Theory and Techniques, Lviv, Ukraine, 2009: 3-12.
[15] Kravchenko V F, Kravchenko O V, Safin A R. Kravchenko-Rvachev probability distribution in the problems of analysis and synthesis for linear arrays. In: Proceedings of International Conference on Antenna Theory and Techniques, Lviv, Ukraine, 2009: 66-69.
[16] Kravchenko V F, Churikov D V. Kravchenko-Kotelnikov-Levitan-Wigner distributions in radio physical applications. In: Proceedings of the International Conference on Days on Diffraction, St.Petersburg, Russia, 2008: 79-84.
[17] Vadzinsky R N. A handbook on the probability distributions. Nauka, St. Peterburg, Russia 2001.
[18] Shirman Y D. Radioelectronic systems: theory and basis of constructing. Radio Engineering, 2007.
[19] Kravchenko V F, Kravchenko O V, Pustovoit V I, et al. Application of the theory of r-functions, atomic and WA-systems of functions in information technologies. In: Proceedings of the 67th Scientific Session Devoted to Day of Radio, Moscow, 2012: 3-8.
[20] Kravchenko V F, Churikov D V. Correlation radar signal processing on basis of probability Kravchenko weight functions. In: Proceedings of IEEE 10th International Conference on Signal Processing Proceedings (ICSP’10), Taiyangdao, Beijing, China, 2010: 1906-1909.
[21] Kravchenko V F, Churikov D V. Kravchenko atomic transforms in digital signal processing. Journal of Measurement Science and Instrumentation, 2012, 3(3): 228-234.
[22] Kravchenko V F, Churikov D V. New WA-system of Kravchenko functions in digital signal processing. Journal of Measurement Science and Instrumentation, 2012, 3(4): 345-351.
date: 2013-03-01
Russian Foundation for Basic Research (No.12-02-90425)
V F Kravchenko(kvf-ok@mail.ru)
CLD number: TN911.7 Document code: A
1674-8042(2013)03-0231-07
10.3969/j.issn.1674-8042.2013.03.007
 Journal of Measurement Science and Instrumentation2013年3期
Journal of Measurement Science and Instrumentation2013年3期
- Journal of Measurement Science and Instrumentation的其它文章
- Test on oxygen and benzene contents in gasoline by mid-infrared spectroscopy*
- Particle-filter-based walking prediction model for occlusion situations*
- Automatic estimation and removal of noise on digital image*
- Application of signal sparse decomposition in dynamic test*
- AC current automatic calibration using two different TCC designs*
- Smart decontamination device for small-size radioactive scrap metal: using abrasion pin in rotating magnetic field and ultrasonic wave cleaner*
