拉伸损伤细观机理的弹性力学分析
崔 崧,陈岚峰
(沈阳师范大学 物理科学与技术学院,沈阳 110034)
0 引 言
损伤力学是研究含缺陷固体材料破坏过程理论的一门学科,它有2个主要分支:连续损伤力学与细观损伤力学,两种方法都有学者作了大量的工作[1-12]。基于细观的唯象损伤理论的研究看来是今后损伤本构理论研究的发展趋势[13],通过对这种宏细观相结合损伤理论的研究,可在材料的细观结构的演化与宏观力学相应之间建立起某种联系。
利用弹性力学理论中平面应力问题的复变函数解答[14-15],在远端受均布拉伸应力的无限大薄板上截取一个含一条裂纹的单元体,可求出单元体在边界及裂纹所在平面处的位移场,通过平均化得到单元体的平均线应变并分析了这种线应变与单元体中裂纹几何尺寸之间的联系,利用弹性拉伸本构关系,可得到弹性拉伸损伤细观机理的某些解释,这种理论是适用于脆性和准脆性材料的,同样的方法已经分析了弹性剪切损伤的细观机理[16]。
1 远端受拉伸薄板内部的位移场
根据弹性力学理论,平面应力情况下的位移分量的复变函数表示式为[14]
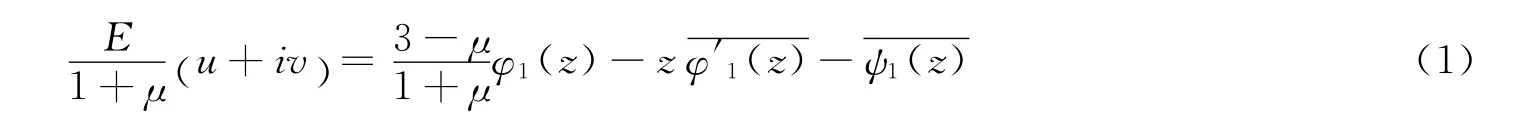
式中:E为材料杨氏模量;μ为泊松比;φ1(z)、ψ1(z)为变量z=x+iy的复变函数。若已知其表达式,代入式(1)中并将右边的实部和虚部分开,便可得到材料内任一点(x,y)的位移分量u和v;
如图1所示,考虑一个内部含一条裂隙的无限大薄板,裂隙沿x方向,长度为2a,远端在垂直于裂隙方向(y向)上受有均布拉伸载荷q,则上式中的复变函数φ1(z)、ψ1(z)可表示为[14]

将式(2)对z求导,可得式(1)中的φ′1(z)。
由式(1)、式(2)、式(3),可求出裂纹面上(y=0)的位移分量v为
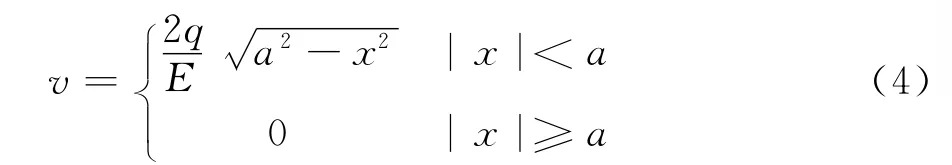
而通过y轴的截面(x=0)上,有位移分量u=0。
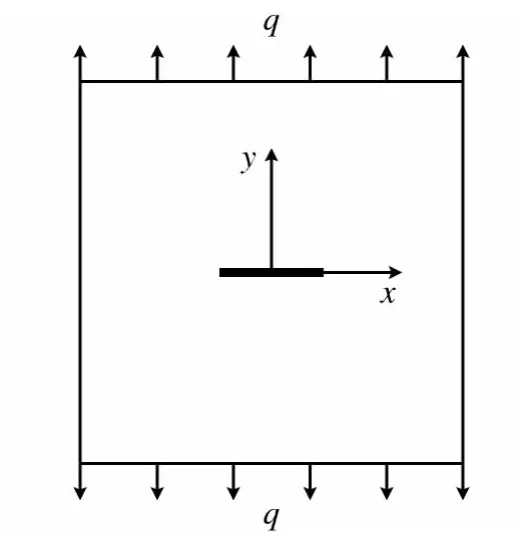
图1 远端受均匀拉伸载荷的薄板
2 含裂纹单元体拉伸本构关系的细观描述
在图1中薄板的裂纹周围截取一块单元体,如图2所示,裂纹对称位于单元体中央,单元体长度为2l,高度为2h。取单元体的四分之一进行分析,如图3所示,设y=h和y=0截面处的位移分量v的平均值分别为和;x=l和x=0截面处的位移分量u的平均值分别为和,则研究对象沿x、y轴的基体平均线应变分别为


图2 中心含裂纹的单元体
在图3中的截面y=h上取多个节点,按式(1)、式(2)、式(3)计算各个节点上的位移分量vi,可得到截面y=h上位移v的平均值=∑vi/n,从而可得到式(5)中沿y轴方向的总体线应变形式如下
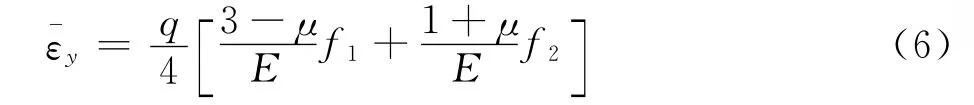
其中,f1,f2是a/l及l/h的函数。
若确定f1的形式,可先令几何尺寸l/h保持一个恒定值不变,通过改变a/l的值,得到不同的f1值,从而确定在恒定的l/h下,f1与a/l的函数关系。例如,取l/h=1时,有f1和a/l的若干个对应点,如图4所示。可设

采用最小二乘法,可确定上式中的参数k2和k3,模拟曲线如图4所示。

图3 单元体的线应变分析

图4 恒定时与的关系
依次取不同的l/h,利用上述弹性理论分别计算f1值,可知在其他l/h值下,f1与a/l的对应函数关系仍然类似于式(7),只是不同的l/h对应于不同的参数值k2和k3。分别计算不同l/h下的参数k2和k3,可得l/h与k2和k3的若干个对应点,分别如图5、图6所示,对应的函数关系都类似于直线,可设
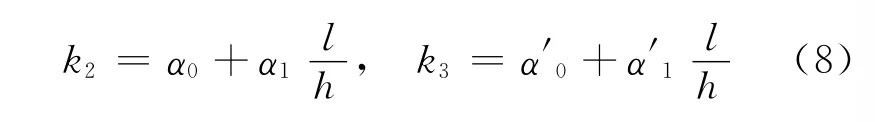
采用最小二乘法,可求得上式中的系数α0、α1、α′0、α′1。模拟的直线分别见图5和图6。将式(8)代入式(7),得
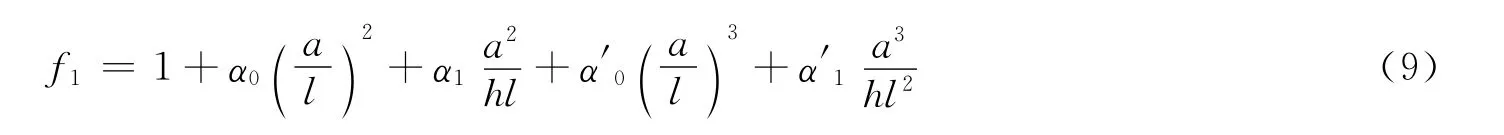

图5 参数与的关系
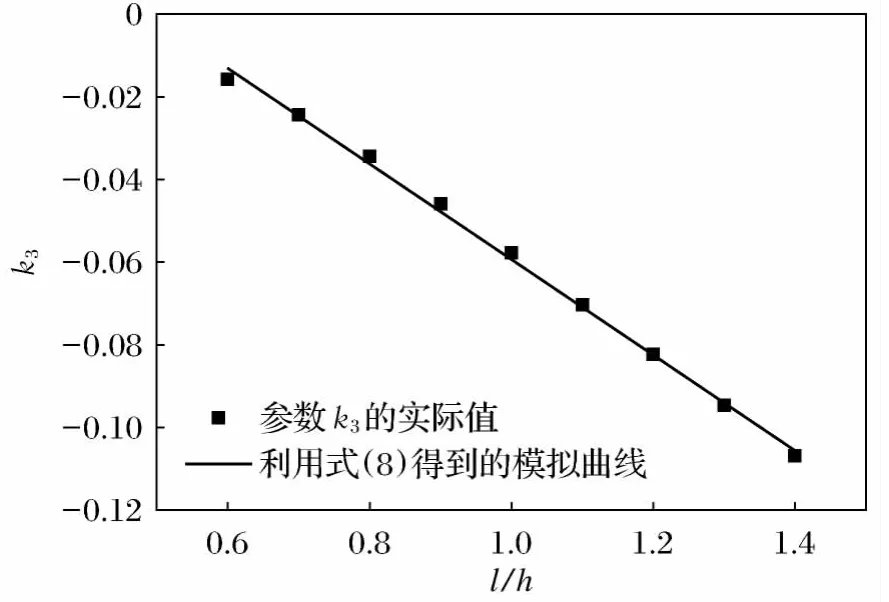
图6 参数与的关系
同理可确定函数f2的形式如下
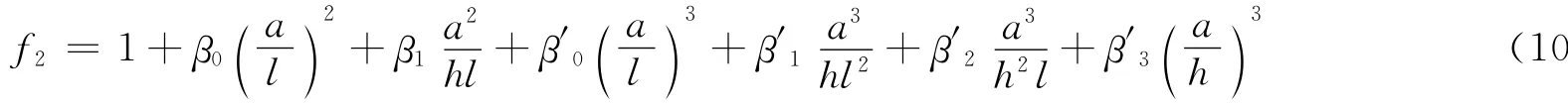
其中,系数β0、β1、β′0β′1β′2和β′3同样可由最小二乘法求出。
由式(6)可得

图3中y=0截面处的位移分量v的平均值可根据式(4)按以下方法计算
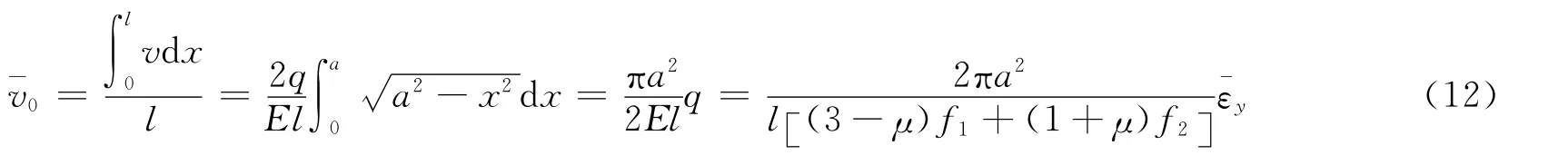
所以沿y轴方向的基体平均线应变为
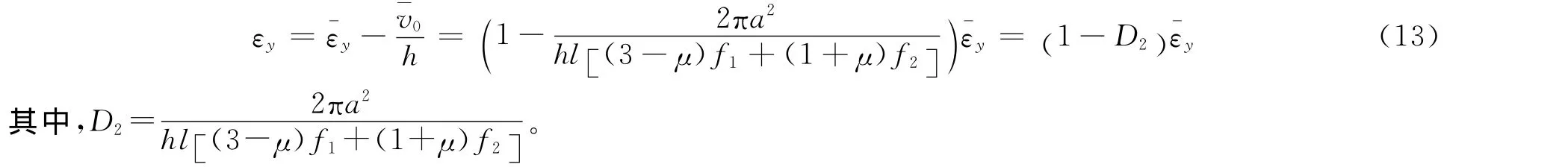
对于脆性和准脆性材料,可以认为到破坏以前其力学行为都是弹性的,所以对于单元体,有
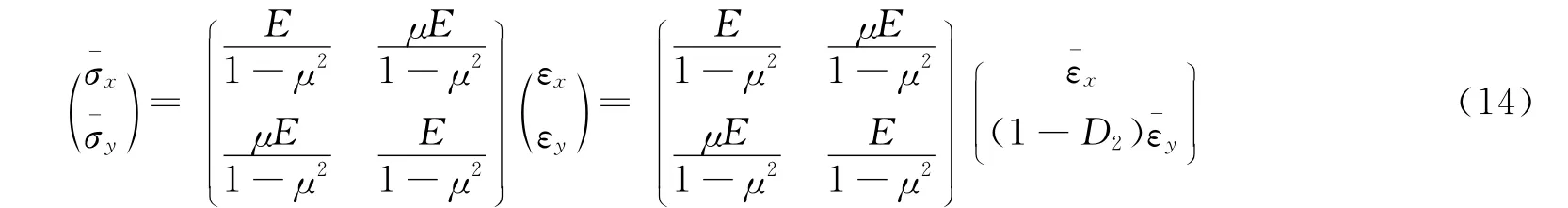
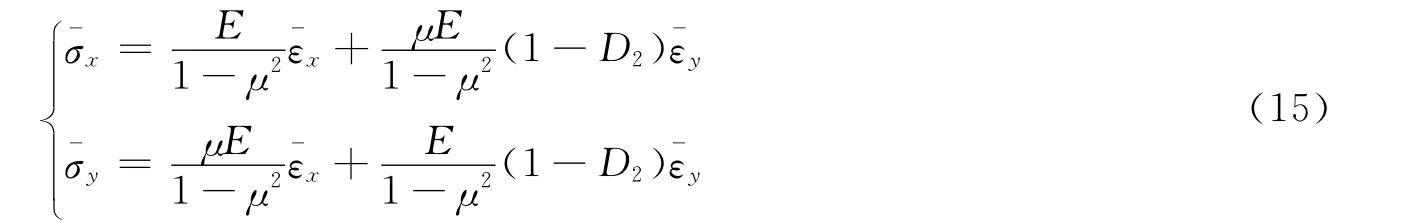
式(15)是给定的应力状态下得到的单元体本构关系,但是可认为适用于裂纹张开时的任何应力状态。设单元体在y轴方向上受单向拉伸,将=0>0代入上式,则可得到
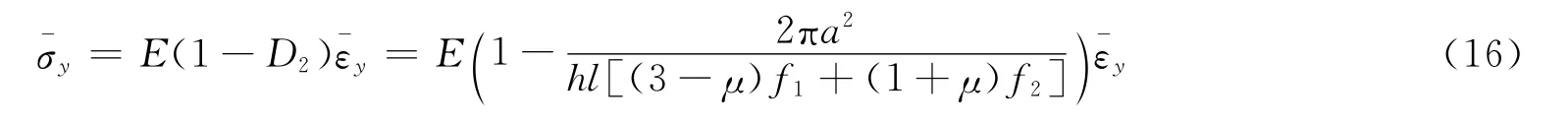
则裂纹体的有效弹性模量为
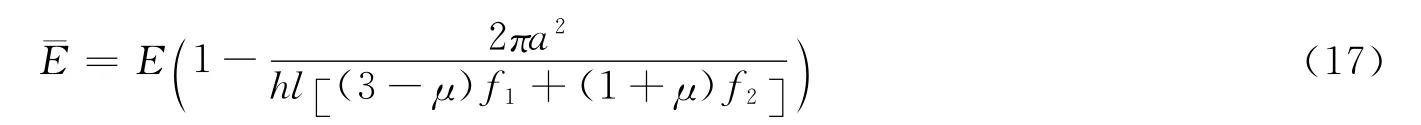
式(16)和式(17)就是脆性和准脆性材料的弹性拉伸损伤的细观机理的描述。
假设此平面问题下的薄板含有若干均匀分布的平行微裂纹,微裂纹半长仍为a,则单位面积内的微裂纹数为N=1/4hl,令微裂纹密度参数f=Na2,利用式(17)可描绘出ˉE/E随微裂纹密度参数f的变化曲线,如图7所示,其中μ=1/3,l/h=1。
3 结 论
利用弹性力学中的复变函数法分析了含裂纹单元体的拉伸应力-应变本构方程,从而解释了拉伸损伤与裂纹及单元体几何尺寸之间的关系,具有较为明确的物理意义,结合之前用相同方法研究过的剪切损伤机理,可建立拉伸与剪切损伤变量之间的某种联系。这种方法可推广至分析含任意方向裂纹单元体的剪切和拉伸细观损伤机理,进一步建立含随机裂纹材料的损伤理论。

图7 弹性模量与微裂纹密度参数的关系曲线
[1]KRAJCINOVIC D,FONSEKA G U.The continuous damage theory of brittle materials[J].J Appl Mech,1981,48(4):809-824.
[2]TALREJA R.Damage development in composites:mechanics and model[J].J Strain Anal Eng,1989,24(4):215-222.
[3]SWOBODA G,YANG Q.An energy-based damage model of geomaterials(part 1and part 2)[J].Int J Solids Struct,1999,36(12):1719-1755.
[4]DRAGON A,HALM D,DESOYER T.Anisotropic damage in quasi-brittle solids:modeling,computational issues and applications[J].Comput Methods Appl Mech Eng,2000,183(3/4):331-352.
[5]BENVENSITE Y.On the Mori-Tanaka's method in cracked solids[J].Mech Res Comm,1986,13(4):193-201.
[6]HUANG Y,HU K,CHANDRA A.A generalized self-consistent mechanics method for microcracked solids[J].J Mech Phys Solids,1994,42(8):1273-1291.
[7]BASISTA M,GROSS D.The sliding crack model of brittle deformation:an internal variable approach[J].Int J Solids Struct,1998,35(5):487-509.
[8]沈真.损伤力学及其在复合材料中的应用[J].力学进展,1985,15(23):147-160.
[9]沈为.复合材料损伤-破坏机制与模型[J].力学与实践,1991,13(3):1-16.
[10]LADEVEZE P,DANTECE L E.Damage modeling of the elementary ply for laminated composites[J].Comp Sci Tech,1992,43(3):257-267.
[11]崔崧,黄宝宗,张凤鹏.准脆性材料的弹塑性损伤耦合模型[J].岩石力学与工程学报,2004,23(19):3221-3225.
[12]冯西桥.脆性材料的细观损伤理论和损伤结构的安定分析[D].北京:清华大学,1995.
[13]余寿文,冯西桥.损伤力学[M].北京:清华大学出版社,1997.
[14]徐芝纶.弹性力学:上册[M].4版.北京:高等教育出版社,2006.
[15]陆明万,罗学富.弹性理论基础:下册[M].2版.北京:清华大学出版社,2001.
[16]崔崧,陈岚峰.剪切损伤细观机理的弹性力学分析[J].沈阳师范大学学报:自然科学版,2013,31(1):21-24.

