非线性函数自定义拟合法处理物理化学实验数据

余训爽，张业中

（长江大学 化学与环境工程学院，湖北 荆州434023）

物理化学实验是以数据测量为主要内容，并对所测实验数据进行科学的、合理的处理，得出某些重要的规律，从而研究物质的物理、化学性质及其化学反应规律。本来实验受测量仪器、测量方法以及外界条件等因素的限制，使得测量值与真实值（实验平均值）之间存在差异；加上一般实验数据繁多，一般的处理方法费时费力，不仅人为带来的误差较大，而且同样的数据由不同实验者处理的结果不尽相同，因此，选择科学合理处理数据的方法显得尤为重要。下面简要的介绍两种改进方法在Origin8.0软件中的实现。

1 实验原理与传统数据处理方法简介

蔗糖在H＋催化作用下水解为一级反应，其动力学方程式为［1－2］：

本实验采用旋光度来代替反应过程中蔗糖溶液浓度的变化时，则式（1）动力学方程可变为如下式子：

ln（at－a∞）对t作图为一直线，由直线斜率可求出速率常数。

2 实验存在的问题

根据蔗糖水解反应实验的特点，本实验主要存在的问题如下［3－4］：

1）测定需要恒温，而一般的旋光仪没有恒温装置，无法进行恒温操作。

2）测定a∞需要在溶液放置两天两夜后才能测定，导致该实验所需的时间长，课时不好安排；或将溶液水浴加热50～60℃（恒温30～40min），该方法操作烦琐，耗时长，并易导致溶液变质，因此存在较大的主观误差的缺陷。

3）Guggenheim法虽不需求a∞即可测出速率常数，但要求数据采样时间间隔为定值，且采样时间间隔足够大，在操作时很难控制。

4）a∞很难准确测定，即使在相同的实验条件下，不同的学生所测得的结果也不尽相同。

5）在数据处理上若手工绘图不仅费时费力，而且误差较大；另外同样的数据由不同学生进行手工处理，其结果可能不同。这样老师无法客观评价实验验结果的好坏。

针对以上五个方面的存在的问题，我们组织学生主要从实验方法上改进，采用Origin8.0软件进行了多种方法的实验数据处理，不仅不需要a∞值，还可屏蔽个别偏差较大的数据点，以降低曲线的偏差，提高数据处理的精确度，从而为客观评价试验结果提供依据；其次，能改变学生被动完成实验的状况，从而提高学生的积极性。

3 实验数据处理过程

本实验按文献［2］的方法进行操作，选取2009级食科30901班一组生实验结果进行分析，其数据见表1。

表1 实验数据记录与处理

2.1 非线性函数自定义拟合及初始化

首先绘制散点图，根据散点图的趋势线判断拟合方式。其步骤如下［5］：选择数据窗口菜单命令［Plot］→［Scatter］→出现［Plot setup］对话框，分别点击“时间t作［X］列”和“旋光度at作［Y］列”，单击OK即可可绘制at－t关系的散点图，如图1所示。

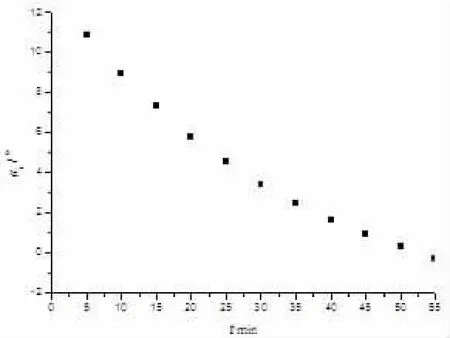
图1 30℃时的at与t的散点图

激活图形窗口1，然后采用F9快捷键或选择菜单命令［Tools］→［Fitti Function Organizer］→单击“New Category”→出现新建自定义函数对话框，输入自定义函数y＝A＋Bexp（－k＊x）→单击“compile”进行公式的调试，调试成功后，单击“Reture to Dialogy”→单击“Save”保存自定义拟合函数→菜单命令［Analysis］→［Fitting］→［Nonlinear Curve Fit］→打开［NLFit］对话框，在“Function”中选择自定义拟合函数，然后单击“Parameters”标签中的“Value”处输入初始值A＝－3.5，B＝15，k＝0.02）→单击“Fixed”按钮调试，重复此操作，直到A＝－3.99，B＝17.11，k＝0.02776为止→单击“Fit”拟合，然后单击“OK”即可。其拟合图（见图2和图3）和方程如下：

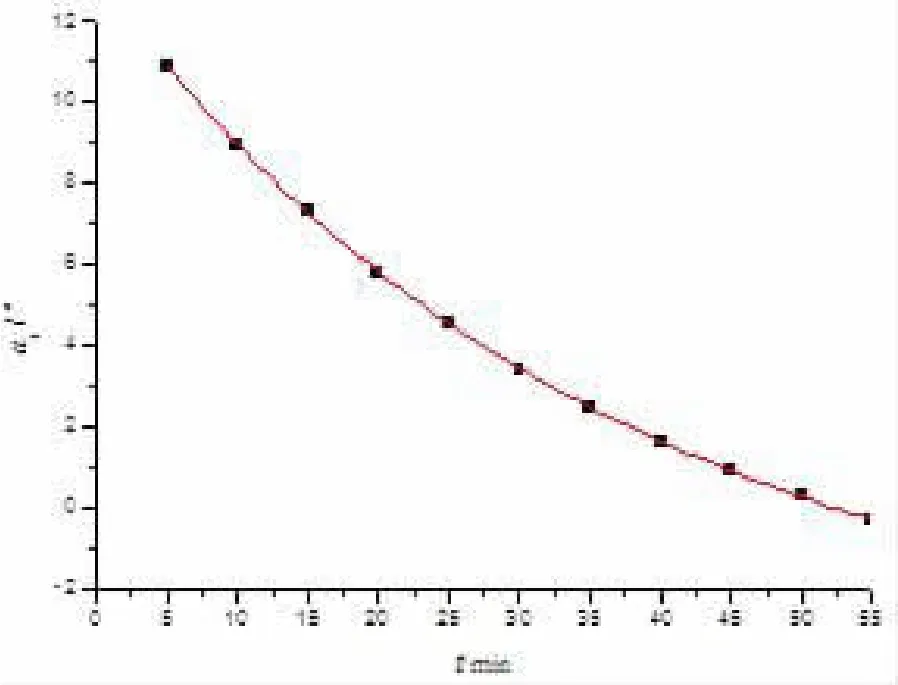
图2 30℃时的自定义拟合图

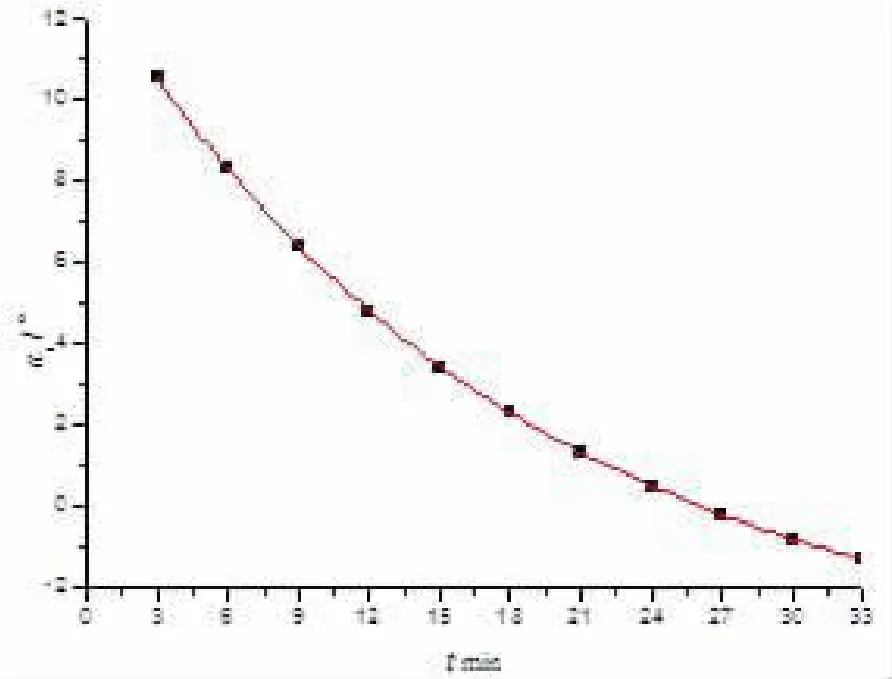
图3 35℃时的自定义拟合图

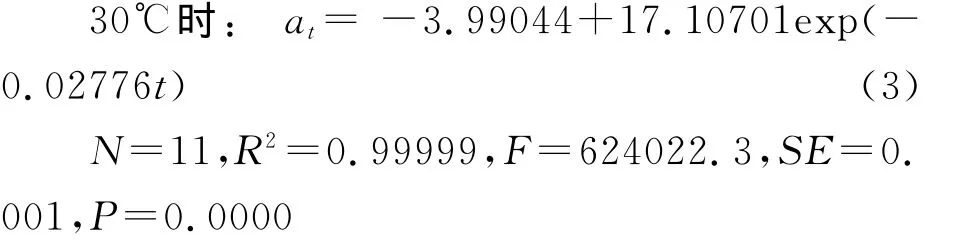
式（3）中，N、R2、F、SE 和P 依次为回归方程的样本数、判定系数、Fischer检验值、标准偏差和显著性水平，下同。

3.2 线性函数自定义拟合及初始化

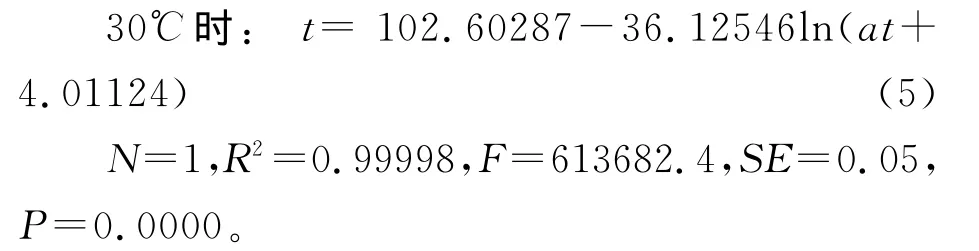
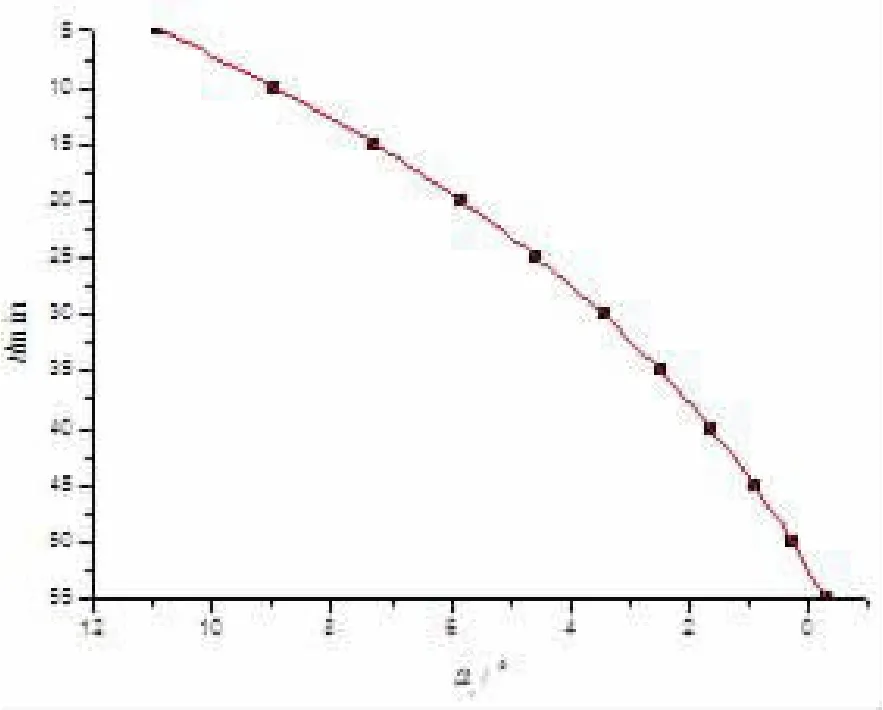
图4 0℃时的t与at－的拟合图

3.3 自定义拟合模型对比

选择菜单命令［Analysis］→［Fitting］→［Copare Datesets...］→出现［Fitting：fitcmpdate］对话框→选择“Fit Result1”和“Fit Result3”→单击“OK”即可完成数据集对比并输出数据比较报表，并自动生成拟合参数分析表（表2）。由表2可知模型（3）优于模型（5）。

从式（3）回归结果来看，判定系数R2＝0.9999（99.99%），说明模型中的样本只有约0.01%的未知因素不能揭示，即属优秀级，表明该模型是有效的，且预测能力强；其次拟合模型的F值远大于10，P＝0.05水平上的显著性检验小于0.0005（文中为P＝0.0000），而且自变量都大于因变量的10倍以上，因此以上方程从统计学的意义上讲也是成立的，模型真实可靠。

表2 拟合参数分析表

4 实验结果的验证

根据文献［6］，盐酸浓度在1～3mo·L－1范围时，蔗糖水解速率常数k与c（H＋）的关系为：

30℃时：k／min－1＝ －1.443×10－2＋2.08×10－2c（H＋）＋7.93×10－3expc（H＋）

35℃时：k／min－1＝ －2.1×10－2＋2.668×10－2c（H＋）＋1.751×10－2expc（H＋）

上述计算结果与理论值基本一致。因此，用此方法处理物理化学数据测定蔗糖水解反应速率常数和活化能是可取的。

5 结束语

传统方法最大的优点是它的直观性，Guggenheim法优点可以不求a∞即可测出速率常数，但各有缺陷。使用Origin8.0软件处理实验数据可以避免以上缺点；其次改进的方法可大大简化数据处理过程并能获得更多的参数信息量，充分发挥软件处理数据客观、直观、快捷、高效、精度高等特点，为客观评价实验结果提供了可靠的依据。本文的方法还可以应用于乙酸乙酯皂化反应速率常数测定、最大气泡法测溶液的表面张力和过氧化氢催化分解速率常数测定等物化实验，因此，以计算机软件处理数据和绘制图形，将是物理化学实验的必然趋势。

［1］付献彩，沈文霞，姚天扬，等.物理化学：下册［M］.5版北京：高等教育出版社，2005.

［2］谢修银.物理化学实验［M］.武汉：武汉大学出版社，2010.

［3］周从山，杨涛.蔗糖水解实验数据处理新方法［J］.实验科学与技术，2008，6（2）：46－48.

［4］李红霞.计算机在物理化学实验数据处理中的应用［J］.实验室科学，2010，13（1）：111－112.

［5］方安平，叶卫平.Origin8.0实用指南［M］.北京：机械工业出版社，2009.

［6］朱艳，杨文春，党微.盐酸催化蔗糖水解中反应速率常数和盐酸浓度等温关系式［J］.天然产物研究与开发，2007，19（6）：1067－1069.

［7］周从山，杨涛，张建策.蔗糖水解实验数据处理与误差分析［J］.大学化学，2008，23（4）：56－59.