时变电磁场惟一性定理的一般证明及其物理解释

孙春峰

（湖北工程学院 物理与电子信息工程学院，湖北 孝感432000）

麦克斯韦方程组是电磁场理论的核心内容，是分析电磁场问题的理论基础。根据这组方程，可以建立实际电磁场初边值问题的表达式，然后用某种方法求出该初边值问题的解。惟一性定理是保证用不同的方法求解麦克斯韦方程组时都能得到同样结果的理论依据。现行的电动力学教科书［1－3］和文献［4－6］对于静电边值问题的惟一性定理和静磁边值问题的惟一性定理的证明讨论较多，臻于完善。而对时变电磁场惟一性定理的证明涉及不多，有些教科书［7－8］虽有讨论，但采用边界上电磁场的零值强条件而不具一般意义；经典的电磁场名著［9－10］讨论了E⇀边值或 H⇀边值的边界条件却忽视了E⇀、H⇀边值情况而存在局限。在时变电磁场情况下，解麦克斯韦方程组以求得时变电磁场的解，在什么样的初始条件和边界条件时才是麦克斯韦方程组解惟一性的最普遍条件？下面对此作些讨论。

1 叠加解的初边值问题

电磁场问题中，若只考察空间某一有限区域内的电磁场，而区域内外都存在场源时，除了由处于这个区域之内的源产生外，还可由这个区域之外的源产生。外部场源的影响反映在区域边界处由外部源所形成的场值上，通过有限区域的边界条件的作用实现。因此，有限区域的电磁场在已知内部场源初始时刻t0区域内任一点的电场、磁场之值和边界上外部场源场值的条件下惟一确定。

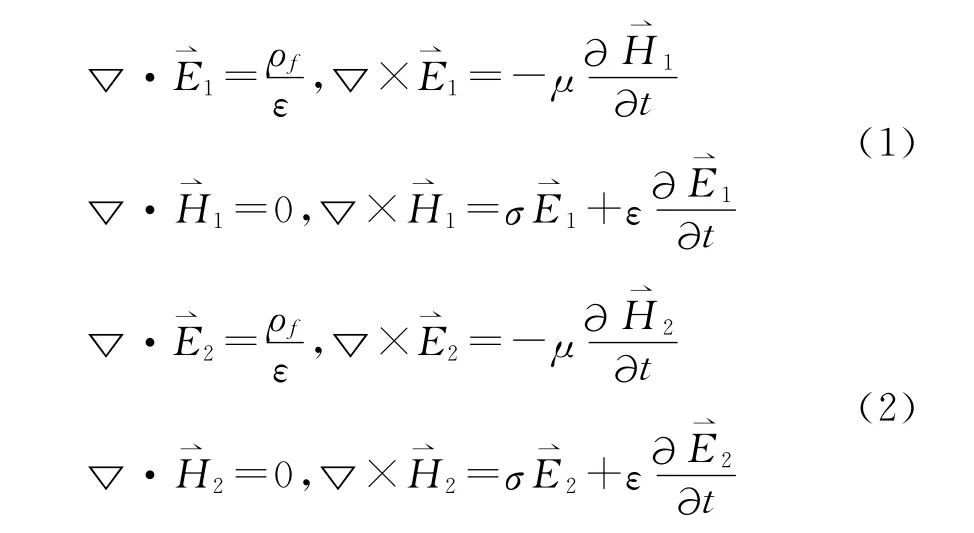
因为是同一场源电磁系统，所以两组方程中的源分布和电磁性质常数ε、μ、σ是相同的。同时，两组方程中的解都满足相同的初始条件和边界条件。即在t＝t0时

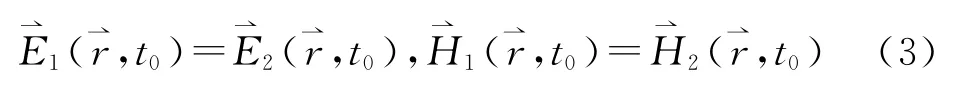
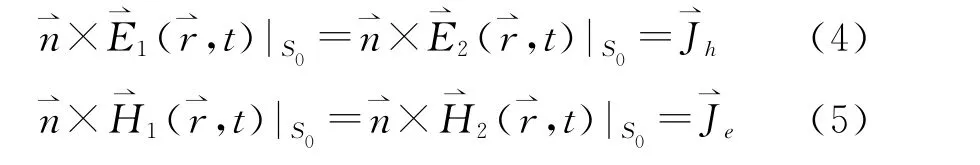
将方程（1）式和方程（2）式对应相减，并令

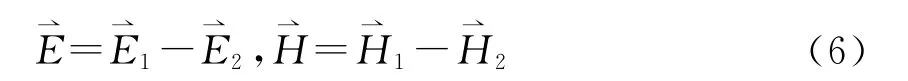
则叠加解（6）式满足的方程组为

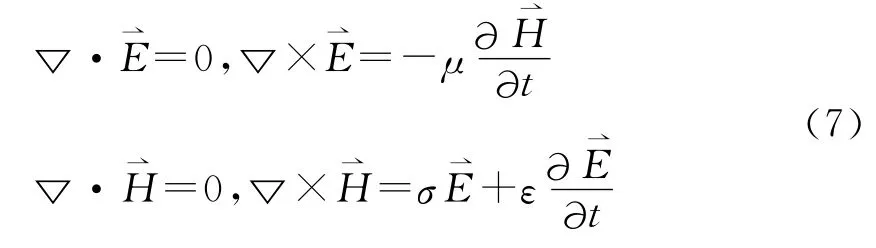
由（3）～（6）式得到方程组（7）式的初始条件和边界条件为

2 有限区域情形

假定区域V 中由V1，V2，…，Vm个子区域组成，分区均匀分布着线性介质，区域V的外边界面为S0；V 内的公共界面分别为S1，S2，…，Sm，如图1所示。每个子区域Vi，（i＝1，2，…，m）中介质 的 电 磁 性 质 常 量εi，μi，σi均 为 大 于 零 的 实常数。

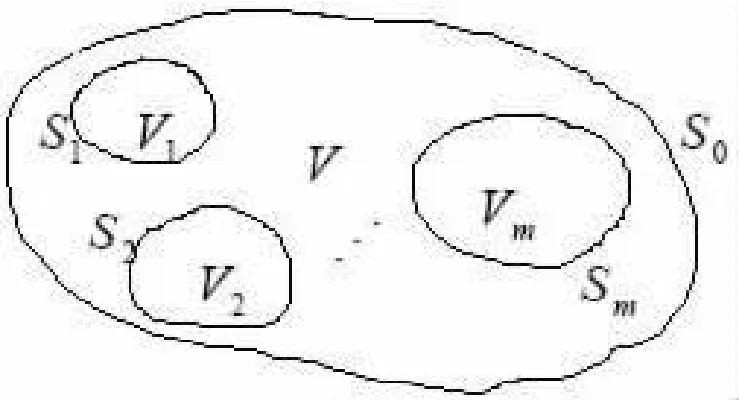
图1 分区均匀的有限区域

图2 无限区域示意图

设Vi中的电场强度为、磁场强度为则V中两相邻的介质区域Vi与Vj，其公共界面Sij上的边值关系表为

设Vi与Vj中的叠加解分别为与、则由（6）式和（10）式得到叠加解满足的子区域边界条件为

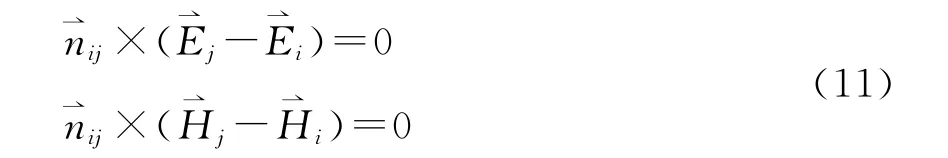
故（8）式、（9）式和（11）式即为V 中叠加解满足的初始条件、外边界条件和子区域边界条件。

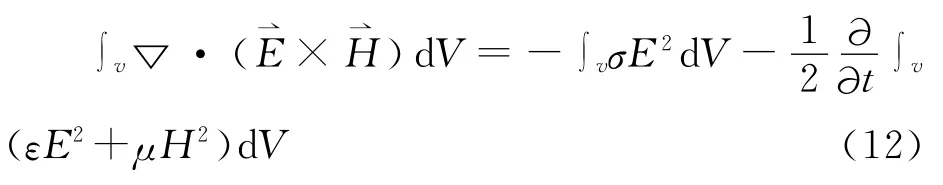
亦即

由（9）式

所以

利用（17）式，对（13）式在t0至t＞t0的时间积分得

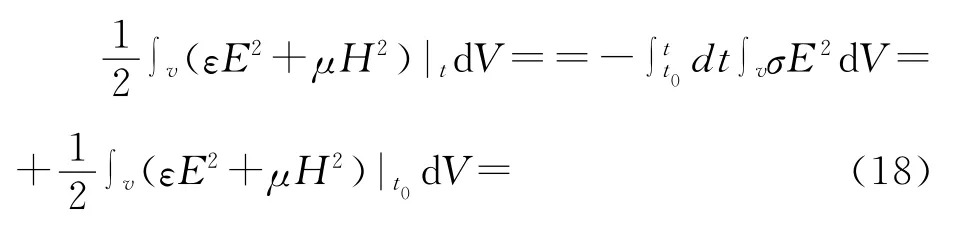
（18）式右边的第1项，因为σ＞0，E2＞0故

（18）式右边的第2项，由（8）式

所以（18）式左边有下式成立

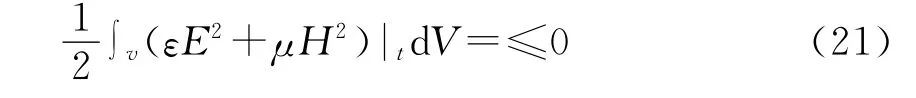
又（21）式左边被积函数中每一项都大于或等于零，其积分必大于或等于零。那么（21）式成立的条件只可能是积分等于零，由此被积函数必等于零，于是

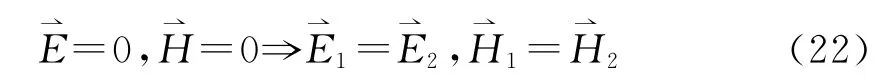
就是说，在给定初始条件和边界条件的区域中，系统内的时变电磁场完全由麦克斯韦方程组惟一确定。

上述数学上的证明结果可以从物理上得到自然解释。因为由子区域边界条件和外边界条件已经证明∫v▽·（）dV＝＝0，因而（13）式可以写为

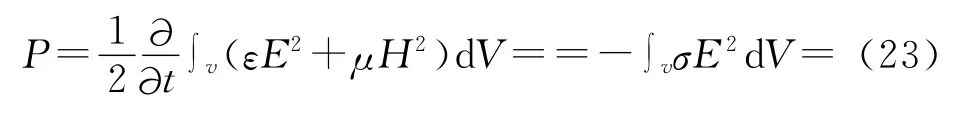
3 无限区域情形

如果所考虑的区域V是一个无限大区域，这可以认为在有限范围内存在一个或几个封闭的边界面S′而不再有其它的边界，如图2所示。

对无限大区域，S′为有限范围的边界面，故S′上的边界条件已知，并有前述（15）式的证明结果；对无限远边界，可任取某一定点为球心，作半径为r的大球面Sr，先考虑包含在Sr和S′之内的区域Vr，再取r→∞的极限，此极限结果即可作为无限区域的结果。这时S0＝S′＋Sr，因而（14）式右边的第1项变为

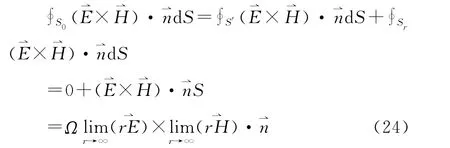
（24）式中Ω为无限大球面S对球心所张开的立体角。

若假定所有场源都位于有限区内，则电磁场在无限远处满足下列条件［11］

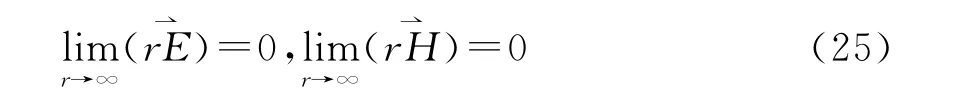
于是（24）式的面积分等于零。类似前述讨论，同样可以得到解的惟一性。

必须指出的是，对无限场域，当场点与场源间的距离充分大时，两个场量的幅值均至少按距离反比减少；事实上，位于有限区域内的场源所产生的场在无限远处均按1／r1＋δ（δ≥0）的规律减少，因此条件（25）恒成立。

以上讨论的是在σ≠0时得到结论。对σ＝0的理想介质，因σE2＝0，此时推不出E＝0的结论。若规定在σ＝0时的任何解都取σ≠0时的解在σ→0时的极限值，由于惟一解的极限只有一个，那么，用这种方式得到的解仍然是惟一的。

若单纯从数学上求σ＝0时麦克斯韦方程组的解，则解不惟一（可能有多个）。如空腔内的自由振荡，不同幅度的振荡都可以存在。然而，实际上任何物理介质都具有不同程度的损耗，把σ→0时的极限值作为小损耗介质是合理的。

4 时变电磁场惟一性定理的表述

综上所述，时变电磁场的惟一性定理表述如下：

在均匀线性各向同性介质的空间区域中，给定t＝t0时刻区域V 内各点电场和磁场的初始值，并同时给定t≥t0时子区域边界条件

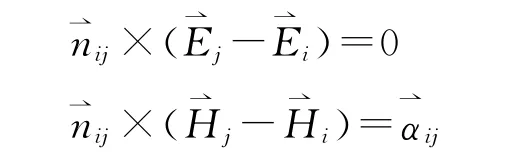
外边界条件

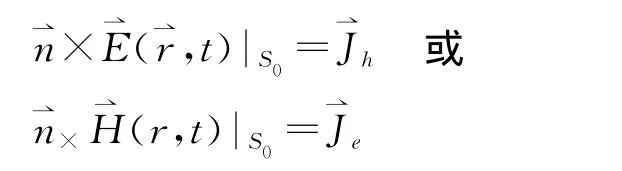
以及无限远条件（只对无限区域情形）

则区域V中的时变电磁场都有惟一解。

惟一性定理不仅指明可用任何方便的方法解电磁场，还可根据该定理建立解电磁场问题的等效原理，使原本不容易求解的电磁场变得比较容易求解。

5 讨论

可见，时变电磁场的初边值问题，只有在某些限定条件下（如线性介质、外边界条件、无限远条件等）应解麦克斯韦方程组以求时变电磁场的解才有可能存在惟一解。因为线性偏微分方程组的初边值问题，在一般情形下并不存在惟一解。

介质的线性特性是时变电磁场初边值问题存在惟一解的前提条件之一，对于非线性介质，一般不存在惟一解。如铁磁质存在磁化曲线和磁滞回线；铁电体存在电滞回线等。

应该指出的是：以上证明讨论的是各向同性线性介质，因为方程组（1）、（2）式默认了介质的宏观电磁性质方程成立的各向同性线性条件。对各向异性的线性介质，沿着上述类似的思路和方法，可以证明时变电磁场惟一性定理仍然成立。

［1］郭硕鸿.电动力学［M］.2版.北京：高等教育出版社，1997.

［2］俞允强.电动力学简明教程［M］.北京：北京大学出版社，1999.

［3］Jackson J D.经典电动力学：上册［M］.朱培豫，译.北京：人民教育出版社，1978.

［4］董超铀.惟一性定理的补充及证明［J］.大学物理，1988（9）：24－25.

［5］姚一民.惟一地确定矢量场的边界条件［J］.大学物理，1988（9）：6－7.

［6］文盛乐.关于稳定磁场惟一性定理的再讨论［J］.大学物理，1991（10）：23－24.

［7］曹昌祺.电动力学［M］.北京：人民教育出版社，1962.

［8］虞福春，郑春开.电动力学［M］.北京：北京大学出版社，1992.

［9］Stratton J A.Electromagnetic Theory［M］.New York：McGraw－Hill，1941.

［10］Harrington R F.Time－Harmonic Electromagnetic Fiel dS［M］.New York：McGraw－Hill，1961.

［11］方能航.电磁理论导引［M］.北京：科学出版社，1986：137－168.