基于神经网络的交流电机调速系统智能算法研究

甘家梁，李志敏，徐翠琴，谈怀江，李 骥

（湖北工程学院 计算机与信息科学学院，湖北 孝感432000）

在工业生产过程中，常规的PID控制器仅适用于线性、定常对象的控制。对非线性、时变特性，耦合及参数和结构不确定的交流异步电机的控制，应用常规的PID控制器不能达到理想的控制效果［1－2］。因为交流电机难以建立精确的数学模型，在线控制受到参数整定方法复杂的困扰，运行过程中往往出现参数整定不良，性能不佳，对运行环境适应性较差。因此，为保证交流电机控制系统获得预期的动态响应，必须设计出鲁棒性强的速度控制方案。由于神经网络具有高度的并行信息处理能力和良好的非线性映射能力，可以用来逼近任何非线性函数［3－5］。如何将BP网络自适应控制与PID控制相结合，寻找一个最佳的KP，KI，KD非线性组合规律，提高在线整定以及优化PID控制器的性能，最终提高矢量控制系统对交流异步电机的控制效果，是一个值得探讨的课题。

1 构建基于BP神经网络PID控制器的模型

1.1 BP神经网络PID控制器的模型

反向传递神经网络（Back－propagation Neural Network，简称BP－NN）是目前神经网络学习模式中最具代表性、应用最普遍的模式，它是通过一元函数的多次复合来逼近多元函数的多层前馈网络，因此，它具有表达任意非线性函数的能力，可以通过在线学习训练获取控制系统参数，实现最佳组合的PID控制信号输出［6－7］。基于BP网络的PID控制器由常规的PID控制器和BP神经网络调节器两个部分组成，控制系统结构如图1所示。

图1 BP网络PID控制器

其中，常规PID控制器直接对交流电机进行闭环控制，借助适当调整比例增益kp（proportional gain）、积分增益ki（integral gain）以及kd（微分增益，derivative gain）三个参数值，使系统稳定并满足系统的规格与性能要求。神经网络能根据系统的在线运行状态，通过自学习和权重系数的自整定后，将目标输出与推论输出误差予以最小化，达到预定的收敛范围，使得神经网络输出层的输出对应于最优控制律下PID控制器3个可调参数kp、ki、kd的输出［8－9］。设 BP神经网络是一个三层的BP网络，其结构如图2所示。

图2 BP网络结构图

增量式数字PID控制算法如下式所示：

其中：△u（t）＝kp（e（t）－e（t－1））＋kie（t）＋kd（e（t）－2e（t－1））＋e（t－2））

为充分反映控制交流异步电机的输入PID控制器信号的特性，输入层神经元个数选为3。u（t）表示受控对象t时刻的输入，x1＝e（k）为k时刻输入信号u（t）和系统输出yout（k）反馈的信号误差量，x2＝∑ki＝1e（k）为反映误差累计的效果，x1＝e（k）－e（k－1）误差的变化率，可以反映误差变化的快慢。

BP神经网络输入层节点的输入为［10－11］：

网络隐含层的输入、输出分别为：

上式中，上角标（1）、（2）、（3）分别表示输入层、隐含层和输出层。为隐含层的权重值。

此处隐含层的神经元的转移函数选择最常用的双弯曲Sigmoid函数：

网络输出层的输入和输出分别为：

因为在PID控制中 一般都是正数，所以输出层神经元的激化函数g（x）选择了非负的双弯曲Sigmoid函数，其定义式为：

设计的控制器采用的是实时训练算法，从电机运行开始到稳态到制动过程，都在实时的自整定网络，也就是每时每刻都采样电机的设定速度和电机速度环实际反馈速度 的误差来训练网络，不断更新整个控制系统的权重值和偏差值，直到网络收敛为止，达到全过程任意时刻PID控制器的参数都处于最优状态［12－13］。因此性能指标函数定义为：

在网络误差反向传播和权重系数调整过程中，为了加速BP网络尽快收敛到局部极值，在权系数值整定时加入动量项：

由分析可知，被控对象交流异步电机是一个具有非线性、强偶合的高阶多变量系统，受控对象的灵敏度不易获得，因此仿真中选择采用符号函数sgn）来代替，可以使矢量控制对电机运行过程中环境的改变、负载的变动以及参数变化所引起的控制环路的扰动等灵敏度降低。在电机参数波动很大时（如转动惯量J缩小或扩大10倍），电机的PID控制器能在线调整比例积分和微分之间的组合，实现高性能的控制。这样BP神经网络PID控制器能独立于系统，具有普遍的应用性。由sgn（）代替所带来的误差影响可以通过调整学习速率来补偿。由上式得：

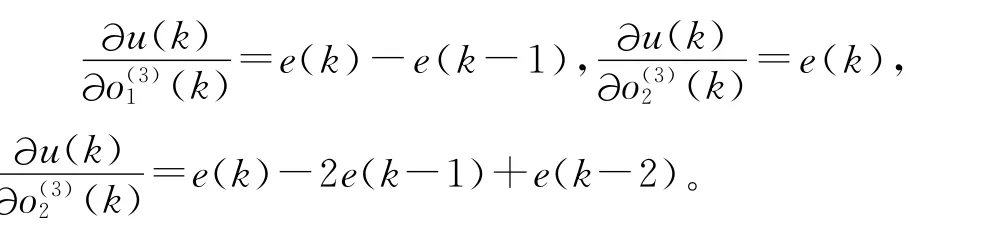
经上述分析，可以推导出输出层的权重系数学习算法表示为：

同理，隐含层的权重系数学习算法表示为：

上式中，g′（·）＝g（x）（1－g（x）），f′（·）＝（1－f2（x））／2。

1.2 引入动量因子改进自适应学习算法应用于BP神经网络

反向传播神经网络具有学习准确度高、反馈速度快的优点。它具有高度的非纯属映射能力，可以代替解非线性方程组或其它复杂的计算。学习过程由信号的前向传播和误差的反向传播两部分组成。为了改善学习过程中的振荡，加快收敛速度，引入自适应学习速率法和动量法。

1.2.1 动量法

引入动量因子α的目的是使网络在修正权重值时，在每一权重值的变化上加上某比例的前一次权重值修正量，增加一个阻尼项，以减少过程振荡，其数学描述如下［14］：

1.2.2 自适应学习速率法

BP神经网络算法在学习训练过程中利用梯度递减法存在着速度收敛慢等问题。为解决此类问题，采用自动调节学习速率方法，其算法可用如下迭代方程描述［15］：

上式中：E（k）和E（k＋1）分别代表第k次和第k＋1次学习训练后的误差平方和。若E（k＋1）＜E（k），说明第k次权重值修正有效，学习速率增加；若E（k＋1）＞E（k），则说明第k次权重值修正无效，则乘以减量因子，减小学习速率，从而减小无效迭代，加快网络学习速度。

2 BP神经网络的PID控制器设计

引入动量因子与自适应学习速率相结合的方法，BP算法的在线学习速率得到了很好的控制。综合以上推导公式，自适应人工神经网络PID控制器归纳出如下步骤：

1）选择输入层节点数为3，令k＝1，设定出各层权重值的初始值、学习速率η和惯性因子α；

2）采样获取电机当前时刻的设定转速rin（k）和速度环反馈速度yout（k），并计算该时刻的权重值与偏差值的变化量；

3）计算BP－NN各层神经元的输入输出权重值，其NN输出层的三个输出变量即为PID控制器的三个可调参数kp、ki、kd；

4）根据下式

uk＝u（k－1）＋kp（e（k－））＋kid（k）＋kd（e（k）－2e（k－1）＋e（k－2）），计算PID控制器的输出u（k）；

5）进行神经网络学习，根据公式（9）～（12）在线调整各层权重系数，实现PID转速控制器参数的自适应调整；

6）置k＝k＋l，返回1），直到误差满足要求为止。

3 系统仿真与实验结果分析

交流异步电机矢量控制系统的仿真平台由四个分模块组成，如图3所示。

图3中，immemo为异步电机模型，controller为控制器模块，其采样周期为100μs，采用SVPWM控制策略实现对电流、速度的控制；compare是逆变器驱动模块，控制逆变器的开关信号由输入的比较值与三角波进行比较得到；inverter为逆变器模块，在开关信号的作用下逆变器输出就得到电机所需的三相交流电压，其中母线电压恒为540V。

在MATLAB／SIMULINK下构建转子磁场定向控制系统。仿真所用电机各项参数为：额定电压VN＝380V，额定电流IN＝15A，额定功率PN＝5.8kW，额定转速nN＝1430r／min，励磁电感Lm＝0.1024H，转子电阻Rr＝0.531Ω，转子电感Lr＝0.1088H，定子电阻Rs＝0.813Ω，定子电感Ls＝0.1063H，转动惯量J＝0.02kg·m2。针对变参数电机模型BP神经网络PID控制器、电机运行中加载时BP－PID控制器与传统PID控制器进行仿真效果对比分析，对改进后的引入动量因子自适应BP神经网络PID控制器进行了仿真测试分析。

3.1 变参数电机模型传统PID和BP神经网络PID控制的控制效果对比

图3 交流异步电机矢量控制系统的仿真平台

实验对照：

本实验给出电机在矢量控制系统中转动惯量（J＝0.2／0.02／0.002）变化情况下，分别被传统PID控制器和BP神经网络PID控制器控制时，启动过程中对比速度响应曲线以及观察在启动过程中BP神经网络控制器的参数自适应变化过程。电机在0.1s时开始启动，设定转速为1500 rad／min。

3.1.1 对比转动惯量在J＝0.02时的控制效果

在J＝0.02时，控制效果如图4和图5所示。

图4 J＝0.02时传统PID控制效果

图5 J＝0.02时BP神经网络PID控制效果

从图4和图5的仿真图上可以看出，对某一特定系统，传统PID控制器在多次调整后能达到比较理想控制效果，基本没超调量，系统响应时间很小，而且负载扰动对系统的影响很小。使用BP神经网络PID控制器控制同一系统也表现良好的控制效果，超调量在可控范围内，不超过3%，上升时间也很小，负载扰动也不大。尽管BP神经网络PID控制器的控制效果不如PID控制器，但也表现出超调量低、收敛速度快、对扰动影响反应小等特点。

图6 BP－PID控制器的输出量iq的变化情况

图7 kp、ki、kd 以及iq 的变化情况

图8 启动刚开始时kp、ki、kd的变化情况

从上述仿真数据可以看出，三相电机在加速初期，速度接近稳态时以及在稳态运行过程中突加负载扰动时，参数kp、ki、kd的改变非常明显，但在加速过程中和达到稳态运行时，三个参数保持基本不变。

3.1.2 对比转动惯量在J＝0.2时控制效果

图9 J＝0.2传统PID控制效果

图10 传统PID控制进入稳态后震荡

图11 J＝0.2时BP神经网络PID控制效果

图12 BP神经网络PID控制进入稳态后

这组仿真是在电机转动惯量J扩大10倍，不改变其它任何参数情况下进行的仿真。一组PID控制器参数在转动惯量J＝0.02时控制效果优良，但在这里控制效果就很不理想。与BP神经网络控制相比，不但上升的时间大了很多，需要相对较长的时间进入稳定状态，而且进入稳态后负载扰动的影响很大，出现了明显的超调量。相比而言，BP神经网络PID控制器的控制效果明显，超调量稳定在与转动惯量J＝0.02时的状态一样。同时，系统在进入稳态运行后，对负载扰动的抗干扰能力很强。

3.1.3 对比转动惯量在J＝0.002时的控制效果控制效果见图13－16。

图13 J＝0.002传统PID控制效果

图14 传统PID控制进入稳态后震荡

图15 J＝0.002时BP神经网络PID控制效果

3.1.4 实验结论

从上述仿真的效果可知，本文所提出的BP神经网络PID控制算法具有较强的适应性和鲁棒性，同时具有在线自学习训练能力，能够动态地调整参数来适应系统以及环境的变化。这在工业控制过程中具有很大的应用价值，对需要迅速更换电机的一些特殊场合不需要进行一步步繁琐的调试。

图16 BP神经网络PID控制进入稳态后效果

3.2 对比电机运行中加载时传统PID和BPPID控制的控制效果

实验对照如下：

电机的设定速度为1500rad／min，在转动惯量（J＝0.02／0.002）变化情况下，30N＊m的负载在1.2s时加上，在运行0.2s后就卸去，对比启动过程中电机速度的响应曲线。

3.2.1 仿真结果

仿真效果见图17、18、19、20。

图17 J＝0.02时传统PID稳态抗扰动效果

图18 J＝0.002时BP－PID稳态抗扰动效果

图19 J＝0.02传统PID稳态抗扰动效果

图20 J＝0.002时BP－PID稳态抗扰动效果

3.2.2 实验结论

从上述仿真效果可知，本文所提出的BP网络神经PID控制算法具有较强抗扰动能力，能较好地适应环境的变化。系统在外部负载突然加上去的情况下，不但不会出现很大震荡，而且能够很快进入稳态。

3.3 测试改进型BP神经网络PID控制器的控制效果

仿真测试环境不变，引进动量因子自适应BP神经网络PID控制器与改进前比较如下：

图21 改进型BP网络PID控制速度仿真效果

图22 改进型BP网络PID控制速度仿真效果

改进型BP神经网络PID控制器的仿真效果如图21和图22。可以看出，控制系统的超调量接近为零，同时，系统的响应速度得到显著提高，负载扰动对运行速度几乎没有影响。同时，在上升过程中，改进型的控制器对环境变化有更灵敏的反应，对误差微小的变化能够作出迅速响应。从电机速度环PID控制器的输出量电流iq可以看出来，iq的大小只能在［－30，30］之间，其上升时间和超调量受到限幅的影响。如果要缩短到达稳态的上升时间，就必须使上升过程中电流iq＝30。而当转速在接近给定转速的时候，迅速调节电机速度环PID控制器的输出电流iq，以便减小超调，使系统稳定。对比两种控制算法的转速仿真结果，可以看出，改进型BP神经网络PID控制系统能迅速准确地对误差信号作出反应。

4 结论

相对于常规的PID控制器而言，基于动量因子自适应学习速率法的BP神经网络PID，运用于交流异步电机的矢量控制中的速度环PID控制器中控制性能更优。实例仿真结果表明，本算法不仅无需对被控对象建立精确的数学模型，而且能借助于改进的算法在线适当调整PID控制器参数的输入、输出信号，实现控制系统性能的最佳，在电机品质参数发生很大变化的情况下仍能表现出良好的控制效果，因此改进型BP神经网络PID控制器的控制策略在工程应用上有较高的实用性。

［1］罗四维.大规模人工神经网络理论基础［M］.北京：清华大学出版社，2004.

［2］赵金，张华军.自学习神经网络权值初始化的贝叶斯方法［J］.计算机应用，2008（S1）：1－4.

［3］丁群燕.智能控制的产生与发展［J］.装备制造技术，2008（11）：125－126.

［4］毕娟，沈凤龙.基于神经网络的交流电机PID控制系统［J］.仪表技术与传感器，2010（2）：98－99.

［5］吴振顺，肖原.零极点配置智能PID控制器在系统控制中的应用［J］.哈尔滨工业大学学报，2008，40（1）：54－57.

［6］侯楚林，王德石.利用PID神经网络实现鱼雷异步交流电机转速辨识［J］.鱼雷技术，2005，13（4）：44－46.

［7］乔维德.改进遗传算法及模糊神经网络在交流伺服系统中的应用研究［J］.电气传动自动化，2008，30（2）：27－30.

［8］Zhao Jinhui，Luo Xiwen，Liu Muhua，et al.Application of BP neural network to sugarcane diseased spots classification［J］.IEEE，2008，3：422－425.

［9］姜毅，郭丙君.基于神经网络PID控制器在交流调速系统中的应用［J］.华东理工大学学报，2012（6）：735－741.

［10］马坦.基于神经网络的交流调速系统智能算法研究［D］.武汉：华中科技大学，2009.

［11］毛坤朋，蔡敢为，董赟.平面二自由度五杆机构BP神经网络整定PID控制［J］.装备制造技术，2010（5）：44－46.

［12］刘金琨.先进PID控制 MATLAB仿真［M］.北京：电子工业出版社，2003.

［13］刘美俊，王耀南.基于参数自适应PID的交流电机智能控制方法研究［J］.电气开关，2004（5）：24－26.

［14］侯媛彬，吕志来，鲁晓辉，等.交流电动机非线性辨识及其智能化控制［J］.煤矿自动化，1998（4）：6－8.

［15］杨威，赵金，张华军.基于再励学习的交流调速系统模糊神经网络控制［J］.微电机，2011（1）：27－30.