一种新的基于椭圆曲线的门限群签名方案

谢 冬,李佳佳,沈忠华

(杭州师范大学理学院,浙江 杭州310036)

一种新的基于椭圆曲线的门限群签名方案

谢 冬,李佳佳,沈忠华

(杭州师范大学理学院,浙江 杭州310036)

在门限群签名体制中,任何t或多于t个成员合作就可以产生一个有效的群签名.基于椭圆曲线离散对数问题的难解性,提出了一个安全、有效的门限签名方案.与现有的基于椭圆曲线离散对数问题的门限签名方案相比,提出的方案具有以下优势：在可信中心TC的帮助下能够追踪到签名者的身份；t个成员合谋攻击不能伪造其他成员的签名也无法获取系统的全部秘密；系统具有一定的稳定性.

数字签名;门限签名;秘密共享;椭圆曲线离散对数

0 引 言

随着信息时代的到来,信息安全的重要性越来越受到人们的关注.数字签名技术被广泛应用于人们生活的各个领域,例如电子商务、大型企业等等.A.Shamir于1979年提出了一种经典的秘密共享方法[1],而后D.Chaum和E.van Heyst于1991年首次提出群签名的概念[2].在群签名体制中,加入秘密共享的思想,便形成了门限群签名体制[3-6].在一个门限群签名方案中,任何t或多于t个成员能够代表整个群去签署任意的消息,但是群中任意少于t个成员不能够合作产生一个有效的群签名.在群公共参数的帮助下,任意的群签名接收者都可以验证签名的有效性,但是他并不知道群中的哪些具体成员参加了此次签名.

在具有相同的安全性水平条件下,椭圆曲线密码体制(ECC)相比于其他的公钥密码体制具有更短的密钥长度.一般说来,一个160比特密钥长度的椭圆曲线密码体制和一个1 024比特密钥长度的RSA密码体制具有相同的安全性.由于椭圆曲线密码体制具有密钥长度短、加解密速度快以及存储空间小等特点,一些基于ECC的具有实际应用的签名方案被相继提出.Wang等提出了一个基于椭圆曲线的可验证的门限数字签名方案[7],此方案中没有可信第三方的参与.Pin-Chang Su等提出了一个基于身份的椭圆曲线门限群签名方案[8].随后,Xia等提出了一个基于ECC的动态门限签名体制[9].然而,上述提到的几个方案均有一个弱点：群中的任意t个成员能够攻破整个系统,获得系统的所有秘密参数,从而能够有效地伪造任意其他t个成员的签名,而整个过程都不会被可信的第三方发现(若方案存在可信第三方).此外,当事后产生纠纷时,一些现有的方案[7-8]并不能追踪到签名者的身份.一些方案也存在稳定性问题,如文献[7].

为了解决以上方案中存在的一些问题,基于椭圆曲线离散对数的难解性,我们提出了一个新的安全、有效的门限签名方案.接下来首先描述新方案，然后给出新方案的安全性和可行性分析，最后给出一个结论.

1 新方案的描述

新方案的安全性是基于椭圆曲线离散对数的难解性.此方案中,可信中心TC负责群私钥、群公钥以及其他系统参数的选取.本方案的所有实体包含可信中心TC、n个群成员以及一个指定的群签名合成者clerk.我们用U表示所有可能参与签名的群成员集合,其中U={P1,P2,…,Pn}.新方案包括系统初始化、(t,n)门限数字签名的产生以及(t,n)门限数字签名的验证3个部分.

1.1 系统初始化

TC通过以下7个步骤来产生系统参数：

1)TC选择一个大素数q,一个GF(q)上的椭圆曲线E：y2=x3+ax+b,其中a,b∈Zq,4a3+27b2≠0modq.

2)TC选择椭圆曲线E上的一个基点G,其中G有足够大的阶p,且满足在由基点G生成的循环群中求解离散对数问题是困难的.

3)TC选择一个安全的单向哈希函数h(·).

4)TC选择一个函数f(x)=at-1xt-1+…+a1x+a0modp,其中ai(i=0,…,t-1)为1到p-1之间的随机整数.

5)我们以f(0)作为群的私钥,TC计算群公钥Y=f(0)G=(xY,yY).

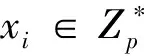
完成以上7个步骤后,TC将xi保密,将ci和di通过安全信道发送给ui,并公开Y和(ui,Yi,Wi,vi).

1.2 (t,n)门限数字签名的产生

若群中t个成员同意参加对于消息m的签名,我们让A表示所有参与签名的t个成员的集合.不失一般性,令A={P1,P2,…,Pt}.门限数字签名产生的整个过程包含份额签名的产生、份额签名的验证以及门限群签名的产生.集合A中的成员和clerk通过以下步骤合作产生(t,n)门限数字签名：

1)集合A中的每个成员Pi计算σi=ciG=(xσi,yσi),并发送xσi给指定的群签名合成者clerk.

2)clerk计算xσiG=(vi′,zi′),并验证vi′是否等于vi.若vi′≠vi,则表明Pi是一个欺骗者.若vi′=vi(i=1,…,t),则clerk用t个签名者的公共值(vi,ui)构造一个身份识别函数F(x),其中

然后clerk将F(x)广播给所有的签名者Pi,其中i=1,2,…,t.

4)集合A中的每个成员Pi首先计算

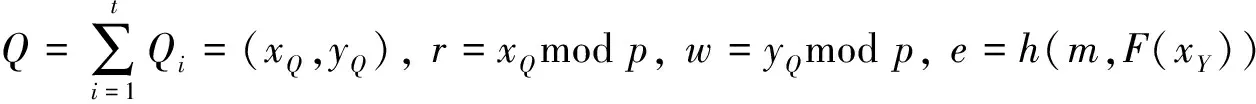
(1)

5)当clerk收集到所有参与签名成员的份额签名后,首先根据式(1)计算e,r和w,然后根据下式是否成立来判断Pi份额签名的有效性：

Gsi+erQi=wBi(Wi+Yi).

通过以上步骤,对于消息m,群成员和clerk共同产生了一个门限群签名(r,s).

1.3 (t,n)门限数字签名的验证

接收到由以上步骤产生的群签名时,接收者首先计算e=h(m,F(xY)),然后验证等式sG+erQ=w(L+Y)是否成立.若等式不成立,则表明存在恶意的成员伪造群签名或者签名并不是由A中的t个成员产生；若等式成立,则签名是有效的.

定理1 若群签名验证等式sG+erQ=w(L+Y)成立,则对于消息m的群签名(r,s)是有效的.

证明根据方程si=wBidi-kiermodp,其中e=h(m,F(xY)),将方程两边同时乘以G,得到

siG=wBidiG-kierG.

因此有

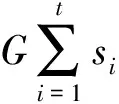
移项得到sG+erQ=w(L+Y),故定理成立.

2 新方案的安全性和可行性分析

1)新方案具有门限特性.任何少于t个成员组成的集合均不能产生一个有效的门限群签名.根据拉格朗日插值定理,只有t个或者多于t个签名者的(ui,di)才能够恢复群私钥f(0).此外,任何少于t个成员也无法完成签名步骤,因为clerk必须收集到t个成员的份额签名才会合成群签名.

2)若指定的签名合成者clerk想要伪造一个身份识别函数F(x),错误的身份识别函数并不能全部满足t个等式F(vi)=ui(i=1,2,…,t)的验证.

3)新方案具有匿名性以及验证简单性.当签名接收者接收到群签名时,在群公钥的帮助下,他可以很简单地验证签名的有效性.在没有可信中心TC的帮助下,接收者也无法知道具体是哪些成员参与了此次签名.

4)新方案能够抵抗伪造攻击.首先,恶意攻击者不能伪造有效的份额签名,因为恶意攻击者并不知道di,所以他不能计算一个有效的si.其次,恶意攻击者并不能直接伪造一个有效的群签名.根据群签名的验证等式sG+erQ=w(L+Y),他不可能伪造一个有效的(r,s)满足验证方程.因为知道r,s中的一个数去求第二个数都是椭圆曲线上的离散对数问题,在计算上是困难的.

5)新方案具有可追踪性.现有的大多基于椭圆曲线的门限签名方案均无追踪性,如文献[7-8].然而,在本方案中,若事后产生了签名纠纷,在TC的帮助下,任何合法的接收者均能追踪到真实签名者的身份.因为clerk通过t个(vi,ui)构造了一个身份识别函数F(x),接收者利用公开的系统参数一一验证等式F(vi)=ui是否成立.若对于某个ui方程成立,则接收者将ui发送给TC,而TC知道ui和用户之间的一一对应关系.因此TC能够揭露真实签名者的身份.

6)新方案具有防冒充性和强壮性.在现有存在的门限方案中,t或者多于t个成员合作能够恢复系统秘密多项式函数f(x).因此,群中任意t或者多于t个成员能够计算其他成员的私钥f(ui),从而能够伪造其他成员的份额签名.但是在本方案中,任何签名小组不能冒充其他小组生成群签名.即使t个成员恢复了秘密多项式f(x),然而他们并不知道xi,因此不能计算其他成员的个人私钥di,他们依然无法伪造群中其他成员的份额签名.也就是说,群中t个成员合作也无法恢复系统所有的秘密参数,本方案具有强壮性.

7)新方案具有一定的稳定性.在新方案中,当群需要增加或者删除一些群成员时,只需要较少地改变系统参数,在计算上是方便的.当一个新成员Pn+1想要加入群时,TC首先选择一个与xi(i=1,…,n)均不相同的整数xn+1,然后计算Wn+1=xn+1G,Yn+1=f(un+1)G.接下来TC随机选择整数cn+1,根据系统初始化的步骤,计算dn+1以及vn+1.然后TC将(cn+1,dn+1)发送给Pn+1,并公开(un+1,Wn+1,vn+1).而整个过程其他成员的参数均未改变.当TC想要从群中删除一个老成员Pj时,通过以下步骤完成：首先,TC选择一个新的秘密多项式f(x)′且满足f(0)′=a0,以及n-1个新的xi′；其次,TC根据系统初始化的步骤产生n-1个新的ci′和di′；最后,TC将(ci′,di′)发送给Pi且公开(ui′,Yi′,Wi′,vi′),其中i=1,2,…,j-1,j+1,…,n.通过以上步骤,群中便删除了成员Pj.

3 结 论

基于椭圆曲线离散对数的难解性,提出了一个新的具有实际应用的门限群签名方案.相对于其他的公钥密码系统,新方案具有密钥长度短、存储空间小以及安全性高等特点.分析表明,提出的方案具有很高的实际应用价值.

[1] Shamir A. How to share a secret[J]. Communications of the ACM,1979,22(4):612-613.

[2] Chaum D, Heyst E. Group signatures[C]//Advances in Cryptology-Eurocrypt’91 Proceeding. Berlin: Springer Verlag,1992:257-265.

[3] Desmedt Y, Frankel Y. Shared generation of authenticator and signatures(extended abstract)[C]//Feigenbaum J. Advances in Cryptology-CRYPTO’91. Berlin: Springer-Verlag,1992:457-469.

[4] Wang G T, Lin C H , Chang C C. Threshold signature schemes with traceable signers in group communications[J]. Computer Communications,1998,21(8):271-276.

[5] Tseng Y M, Jan J K. Attacks on threshold signature schemes with traceable signatures in group communications[J]. Computer Communications,2000,23(5):771-776.

[6] Wang Guilin, Qing Sihan. Weaknesses of some threshold group signature scheme [J]. Journal of Software,2000,11(10):1326-1332.

[7] Wang Huaqun, Zhao Junxi, Zhang Lijun. Verifiable (t,n) threshold signature scheme based on elliptic curve[J]. Wuhan University Journal of Natural Sciences,2005,10(1):165-168.

[8] Su P C, Chang H K C, Lu E H. ID-based threshold digital signature schemes on the elliptic curve discrete logarithm problem[J]. Applied Mathematics and Computation,2005,164(3):757-772.

[9] Xia Xiangsheng, Hong Fan, Geng Yongjun,etal. Efficient dynamic threshold group signature scheme based on elliptic curve cryptosystem[J]. Journal of Southwest Jiaotong University :English Edition,2008,16(1):18-23.

ANewThresholdSignatureSchemeBasedonEllipticCurveCryptosystem

XIE Dong, LI Jiajia, SHEN Zhonghua

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

In the threshold group signature cryptosystem, any t or more than t members can cooperate to produce a valid group signature. Based on the difficulty of solving the ECDLP(elliptic curve discrete logarithm problem), a secure and efficient threshold scheme was proposed. Comparing to the existing threshold signature scheme based on the ECDLP, this scheme has some advantages ,it is able to track the signer’s identity with the assistance of the trusted center TC,tmembers in the group can not forge other members’ partial signature and can not obtain all the system’s secrets, and the system has certainly stability.

digital signature; threshold signature; secret sharing; elliptic curve discrete logarithm

2012-04-19

浙江省自然科学基金项目(Y6110782).

沈忠华(1973—),男,教授,主要从事数论与密码学、信息安全技术等研究.E-mail: ahtshen@126.com

10.3969/j.issn.1674-232X.2013.01.011

TP309MSC2010: 94A60

A

1674-232X(2013)01-0057-04