π-余代数的楔积
周丽娜,李金其,郑清月
(浙江师范大学数理与信息工程学院,浙江 金华 321004)
π-余代数的楔积
周丽娜,李金其,郑清月
(浙江师范大学数理与信息工程学院,浙江 金华 321004)
给出了π-余代数C上的楔积XαΛYβ的概念,把余代数上楔积的相关性质推广到π-余代数上.研究了π-余代数C上π-子余代数、π-余理想的性质,给出了XΛY与它们之间的联系.
π-余代数;楔积;π-子余代数;π-余理想
本文中,设π是一个乘群,k是一个域,所有的空间都是k上线性空间,映射首先是k-线性映射,⊗是指⊗k.
定义1[1]一个π-余代数C=({Cα}α∈π,Δ,ε)是指一族空间C={Cα}α∈π以及一族映射Δ={Δα,β:Cαβ→Cα⊗Cβ}α,β∈π和映射ε:C1→k,满足
1) (Δα,β⊗ΙCr)Δαβ,r=(ΙCα⊗Δβ,r)Δα,β r;
2) (ΙCα⊗ε)Δα,1=ΙCα=(ε⊗ΙCα)Δ1,α.
从定义知道(C1,Δ1,1,ε)是通常意义下的余代数.
定义2设C=({Cα}α∈π,Δ,ε)是π-余代数,X={Xα|Xα⊆Cα}α∈π和Y={Yβ|Yβ⊆Cβ}β∈π是C的子空间族,则XαΛYβ是指下列线性映射合成的核:
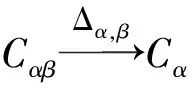
即XαΛYβ=ker(πXα⊗πYβ)Δα,β.


设V,W是线性空间,定义线性映射ρV,W:V*⊗W*→(V⊗W)*为对任意的v∈V,w∈W,v*∈V*,w*∈W*,ρV,W(v*⊗w*,v⊗w)=〈v*,v〉〈w*,w〉.则ρV,W为单线性映射.此时记V*⊗W*⊆(V⊗W)*.
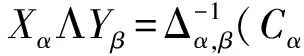

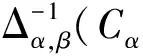
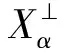


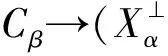
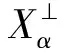

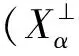
因此,对任意的xαβ∈XαΛYβ,由(πXα⊗πYβ)Δα,β(xαβ)=0,得
Δα,β(xαβ)∈ker(πXα⊗πYβ)=Cα⊗Yβ+Xα⊗Cβ.
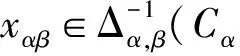
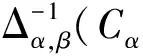
所以
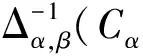
定义4[1]一个π-代数A=({Aα}α∈π,m,μ)是指一族空间A={Aα}α∈π以及一族映射m={mα,β:Aα⊗Aβ→Aαβ}α,β∈π和映射μ:k→A1,满足
1)mαβ,γ(mα,β⊗IAγ)=mα,βγ(IAα⊗mβ,γ);
2)mα,1(IAα⊗μ)=m1,α(μ⊗IAα).
从定义知道(A1,m1,1,μ)是通常意义下的代数.
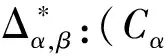
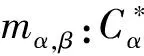


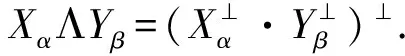
证明根据定义3,可以得到:
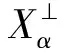

命题4设X={Xα|Xα⊆Cα}α∈π,Y={Yβ|Yβ⊆Cβ}β∈π,Z={Zγ|Zγ⊆Cγ}γ∈π是π-余代数C的子空间族,则
(XαΛYβ)ΛZγ=XαΛ(YβΛZγ)=ker((πXα⊗πYβ⊗πΖγ)((Δα,β⊗ICγ)Δαβ,γ)).
证明由命题1可得
Δαβ,γ((XαΛYβ)ΛZγ)=(XαΛYβ)⊗Cγ+Cα,β⊗Zγ.
(1)
对式(1)两边同时作用Δα,β⊗ICγ,得
(Δα,β⊗ICγ)Δαβ,γ((XαΛYβ)ΛZγ)=Cα⊗Yβ⊗Cγ+Xα⊗Cβ⊗Cγ+Cα⊗Cβ⊗Zγ.
(2)
对式(2)两边同时作用πXα⊗πYβ⊗πΖγ,得
(πXα⊗πYβ⊗πΖγ)(Δα,β⊗ICγ)Δαβ,γ((XαΛYβ)ΛZγ)=0.
从而
((XαΛYβ)ΛZγ)=ker((πXα⊗πYβ⊗πΖγ)(Δα,β⊗ICγ)Δαβ,γ).
同理,
(XαΛ(YβΛZγ))=ker((πXα⊗πYβ⊗πΖγ)(Δα,β⊗ICγ)Δαβ,γ).
由(Δα,β⊗ICγ)Δαβ,γ=(ICα⊗Δβ,γ)Δα,βγ,得(XαΛYβ)ΛZγ=XαΛ(YβΛZγ).
命题5设X={Xα|Xα⊆Cα}α∈π,V={Vα|Vα⊆Cα}α∈π,Y={Yβ|Yβ⊆Cβ}β∈π,W={Wβ|Wβ⊆Cβ}β∈π是π-余代数C的子空间族,且满足对任意的α,β∈π,有Xα⊆Vα;Yβ⊆Wβ,则XαΛYβ⊆VαΛWβ.
证明对任意的xαβ∈XαΛYβ,则Δα,β(xαβ)∈Xα⊗Cβ+Cα⊗Yβ⊆Vα⊗Cβ+Cα⊗Wβ.从而xαβ∈ker((πνα⊗πwβ)Δα,β).故XαΛYβ⊆VαΛWβ.
命题6设X={Xα|Xα⊆Cα}α∈π是π-余代数C的子空间族,则XαΛ(kerε)=Xα=(kerε)ΛXα.
证明

(3)
由
Cα/Xα⊗C1/kerε≅Cα/Xα⊗k≅Cα/Xα
,
则式(3)可以改写为:
同理可得(kerε)ΛXα=Xα.从而XαΛ(kerε)=Xα=(kerε)ΛXα.
由命题5,6可得:
命题7设Y={Yβ|Yβ⊆Cβ}β∈π是π-余代数C的子空间族,若Y1⊆kerε,则XαΛY1⊆Xα,Y1ΛXα⊆Xα.
定义5[1]设C=({Cα}α∈π,Δ,ε)是π-余代数,X={Xα|Xα⊆Cα}α∈π是C的子空间族,若对任意的α,β∈π,有Δα,β(Xα,β)⊆Cα⊗Xβ+Xα⊗Cβ,且ε(X1)=0.称X是C的π-余理想.若对任意的α,β∈π,Δα,β(Xα,β)⊆Cα⊗Xβ,称X是C的左π-余理想.若对任意的α,β∈π,Δα,β(Xα,β)⊆Xα⊗Cβ,称X是C的右π-余理想.
定理1若X={Xα|Xα⊆Cα}α∈π是π-余代数C的左(右)π-余理想,则XΛY={(XΛY)ν}ν∈π是C的左(右)π-余理想,且X⊆YΛX(X⊆XΛY).

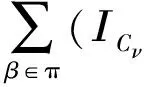
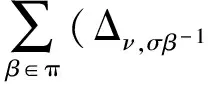
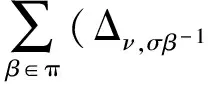
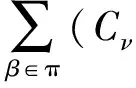
(4)
对式(4)两边同时作用(ΙCν⊗πXσβ-1⊗πYβ),得到(ΙCν⊗πXσβ-1⊗πYβ)(ΙCν⊗Δσ)Δν,σ((XΛY)νσ)=0.即,对任意的ν,σ,有Δν,σ(XΛY)νσ⊆Cν⊗(XΛY)σ.因此,XΛY是C的左π-余理想.
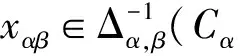
同理可得,若X={Xα|Xα⊆Cα}α∈π是C的右π-余理想,则XΛY是C的右π-余理想,且X⊆XΛY.
定义6[1]设C=({Cα}α∈π,Δ,ε)是π-余代数,X={Xα|Xα⊆Cα}α∈π是C的子空间族,称X是C的π-子余代数,若对任意的α,β∈π,有Δα,β(Xαβ)⊆Xα⊗Xβ.
定理2若X={Xα|Xα⊆Cα}α∈π是π-余代数C的左π-余理想,并且Y={Yβ|Yβ⊆Cβ}β∈π是π-余代数C的右π-余理想,则XΛY是C的π-子余代数.
证明由条件知,对任意的α,β∈π,有
Δα,β(Xαβ)⊆Cα⊗Xβ,Δα,β(Yαβ)⊆Yα⊗Cβ.
由定理1可得
Δν,σ(XΛY)νσ⊆Cν⊗(XΛY)σ,Δν,σ(XΛY)νσ⊆(XΛY)ν⊗Cσ.
从而
Δν,σ(XΛY)νσ⊆((XΛY)ν⊗Cσ)∩(Cν⊗(XΛY)σ)⊆(XΛY)ν⊗(XΛY)σ.
因此,对任意的ν,σ∈π,有
Δν,σ(XΛY)νσ⊆(XΛY)ν⊗(XΛY)σ.
即XΛY是C的π-子余代数.
定理3若X={Xα|Xα⊆Cα}α∈π,Y={Yβ|Yβ⊆Cβ}β∈π是π-余代数C的π-子余代数,则XΛY是C的π-子余代数,且X+Y⊆XΛY,其中X+Y={Xα+Yα}α∈π.
证明由条件知,X是C的左π-余理想,Y是C的右π-余理想.由定理2知,XΛY是C的π-子余代数.
由条件知,X是C的右π-余理想,Y是C的左π-余理想.由定理1知,X⊆XΛY;Y⊆XΛY.因此,X+Y⊆XΛY.
[1] Virelizier A.Hopf group-coalgebra[J].Journal of Pure and Applied Algebra,2002,171:75-122.
[2] Sweedler M E.Hopf algebra[M].New York:Benjiamin,1969.
[3] 方小利,李金其.关于π-余代数的几个性质[J].绍兴文理学院学报,2004,24(7):41-44.
TheWedgeofπ-coalgebras
ZHOU Lina, LI Jinqi, ZHENG Qingyue
(College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua 321004, China)
This paper introduced the notion ofXαΛYβof π-coalgebras, generalized the properties of the wedge of coalgebras to the π-coalgebras, studied some properties ofC-π-subcoalgebras andC-π-coideals, and provided the relations betweenXΛYand them.
π-coalgebras;wedge;π-subcoalgebras;π-coideals
2013-05-12
国家自然科学基金项目(11271319).
李金其(1964—),男,教授,主要从事Hopf代数等方面研究.E-mail:lijinqi@zjnu.cn
10.3969/j.issn.1674-232X.2013.06.005
O153.3MSC201016T99
A
1674-232X(2013)06-0503-04

