保序部分单变换半群的自同态
高京南,杨秀良
(杭州师范大学理学院,浙江 杭州 310036)
保序部分单变换半群的自同态
高京南,杨秀良
(杭州师范大学理学院,浙江 杭州 310036)
设n为正整数,令IOn表示Xn= {1,2,…,n}上所有保序部分单变换在复合运算下而成的半群,刻画了IOn上的所有自同态.
保序部分单变换;自同态;同余
1 引言和预备知识
令Xn={1,2,…,n}, 其中n≥1. 设ISn是由Xn上所有部分单变换组成的集合, 则ISn关于变换的复合运算构成一个半群, 称这个半群为Xn上的对称逆半群.本文的映射是右映射. 设α是ISn中的一个元素, 若对所有的i,j∈dom(α), 如果ilt;j, 就有(i)αlt;(j)α, 则称α为保序部分单变换.ISn中的所有保序部分单变换构成一个半群, 称为保序部分单变换半群, 记为IOn.IOn中的所有幂等元构成的集合记为E(IOn). 显然IOn中幂等元与幂等元的复合仍是幂等元. 保序部分单变换半群是半群理论中很重要的一个部分, 它的许多性质已经被前人研究[1-4].
S为半群,φ:S→S为映射. 若对任意的x,y∈S, 都有 (x)φ(y)φ=(xy)φ, 则称φ为半群S的自同态.S的所有自同态构成的半群记为End(S). 双射自同态称为自同构.特别的, O. Ganyushkin等于2003年在[4]中已经证出IOn的自同构只有两个, 即恒等映射和*:a→a*,其中

i1lt;i2lt;…lt;ik且j1lt;j2lt;…lt;jk. 本文将这一结果推广到自同态.
首先介绍一些符号. 记α的定义域为dom(α),α的像集记为im(α). im(α) 中元素的个数称为α的秩, 记为r(α).LA表示IOn中定义域为A的幂等元, 其中A⊆Xn. 记空变换为0, 恒等变换为1n, 即
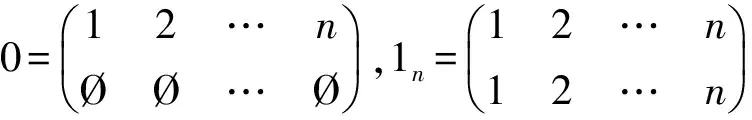
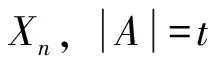
2 主要结果
定理1 令φ:IOn→IOn为任一映射,φ是IOn的自同态当且仅当φ是下面之一:
(1)φ为自同构, 则φ为恒等映射或*:a→a*,其中
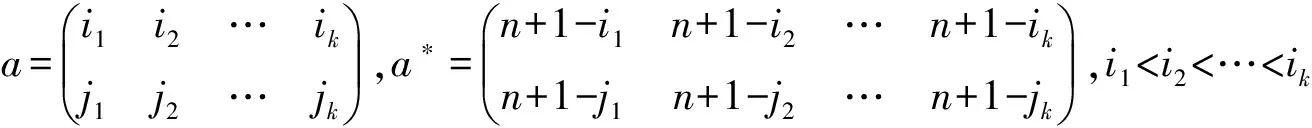
(2)存在幂等元e,f∈E(IOn), 其中e≠f且ef=fe=f, 有(1n)φ=e, (IOn{1n})φ=f;
(3)(α)φ=e, 对任意的α∈IOn均成立, 其中e∈E(IOn).并记这样的φ为φe;
3 定理1的证明
为证明此定理, 首先引入下面两个引理.
引理1 任取e1≠e2∈Gt, 则e1e2=e2e1∈It-1.

同理可得e2e1=LA. 从而e1e2=e2e1∈It-1.
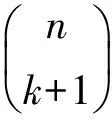

任取α≠β∈(Gk+1)φ, 则存在γ≠δ∈Gk+1,使得α=(γ)φ,β=(δ)φ. 由引理1可知,γδ=δγ∈Ik, 故αβ=(γ)φ(δ)φ=(γδ)φ=η,βα=(δ)φ(γ)φ=(δγ)φ=η. 从而αβ=βα=η.
容易验证定理1给出的映射均是IOn的自同态, 故只需证明IOn的所有自同态均可表示成定理1给出的其中某种形式.
令φ为IOn的自同态. 若φ为自同构, 由[4]知φ满足形式(1).假设φ不是IOn的自同构, 则Kerφ={(a,b)∈IOn×IOn: (a)φ=(b)φ} 为IOn上的一个同余, 由[2]知,Kerφ为Rees同余,且IOn的所有理想均为Ik={α∈IOn:r(α)≤k}, 0≤k≤n.故存在0≤k≤n, 使
Kerφ=ρIk=(Ik×Ik)∪{(a,a):a∈IOnIk}.
当k=0时,Kerφ的每个同余类皆为单元素集, 此时φ为恒等映射, 满足形式(1);当k=n时, Kerφ只有一个同余类, 为In, 此时φ满足形式(3) ; 当k=n-1时, Kerφ共有两个同余类, 分别为In-1,1n, 此时满足形式(2).故只需讨论1≤k≤n-2时的情况.
当1≤k≤n-2时, 由 Kerφ=ρIk=(Ik×Ik)∪{(a,a):a∈IOnIk} 知Ik为Kerφ的一个同余类. 故可设(Ik)φ=τ, 其中τ∈IOn为幂等元. 不失一般性, 令r(τ)=i, 其中0≤i≤n.
任取α∈(Gk+1)φ, 则存在β∈Gk+1, 使α=(β)φ. 任取γ∈Ik, 有τ=(γ)φ, 且βγ,γβ∈Ik,故可得ατ=(β)φ(γ)φ=(βγ)φ=τ,τα=(γ)φ(β)φ=(γβ)φ=τ, 因此ατ=τα=τ.
因同态保持D类, 故Dk+1在φ下的像应包含在IOn的某个D类中,不妨设为Dx, 其中0≤x≤n. 对任意的α∈(Gk+1)φ,由τα=τ可知,im(τ)⊆im(α), 故x≥i. 假设x=i, 则有im(τ)=im(α). 由引理2可知,α是幂等元, 故α=τ.从而(Gk+1)φ=τ, 也即Gk+1与Ik包含于Kerφ的同一个同余类中,这是不可能的. 故假设不成立, 有xgt;i, 即(Dk+1)φ⊆Dx,其中ilt;x≤n.


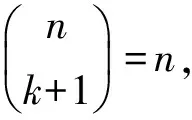
下面又分3种子情形:
情况2.1 设(In-2)φ=e0, 显然e0为幂等元, 假设0≠e0=LA.令δ1,δ2, …,δn∈Gn-1, 其中dom(δi)=Xn{i} . 则δiδj∈In-2,i≠j. 设(δi)φ=LAi,i=1, 2, …,n.
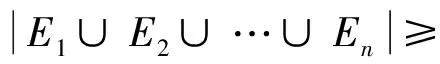
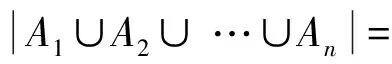
情况2.3 任取e∈Dn-1, 且e为幂等元. 不妨设e=L{ie}′, 其中 {ie}=Xdom(e). 因(Dn-1)φ⊂D1, 故可设(e)φ=aje.现定义π:Xn→Xn如下:(∀i∈Xn)(ie)π=je.则π是Xn上的双射, 且对任意的i∈Xn, 都有(L{i}′)φ=a(i)π.

故k=n-2时, 具有形式(4).
综上所述, 定理得证.
[1]Cowan D F, Reilly N R. Partial cross-sections of symmetric inverse semigroups[J]. Int J Algebra Comput,1995,5(3):259-287.
[2]Fernandes V H. The monoid of all injective order preserving partial transformations on a finite chain[J]. Semigroup Forum,2001,62(2):178-204.
[3]Garba G U. Nilpotents in semigroups of partial one-to-one order-preserving mappings[J]. Semigroup Forum,1994,48(1):37-49.
[4]Ganyushkin O, Mazorchuk V. On the structure ofIOn[J]. Semigroup Forum,2003,66(3):455-483.
EndomorphismoftheOrder-preservingPartialSingularTransformationSemigroups
GAO Jingnan, YANG Xiuliang
(College of Science, Hangzhou Normal University, Hangzhou 310036, China)
Letnbe a positive integer. LetIOndenote the semigroup generated by the compound operation of order-preserving partial injective transformation onXn={1,2,…,n}. This paper described all endomorphisms onIOn.
order-preserving partial injective transformation; endomorphism; congruence
2012-12-14
杨秀良(1963—),男,教授,主要从事半群代数研究.E-mail:yxl@hznu.edu.cn
10.3969/j.issn.1674-232X.2013.03.006
O152.7MSC2010: 43A22
A
1674-232X(2013)03-0220-03

