复域差分和差分方程的研究
陈宗煊, 黄志波
(华南师范大学数学科学学院,广东广州 510631)
复域差分和差分方程的研究
陈宗煊*, 黄志波
(华南师范大学数学科学学院,广东广州 510631)
介绍了近十年来复域差分、q-差分、差分方程及q-差分方程的主要研究成果,其中包括亚纯函数对数导数引理的差分模拟;Clunie引理和Mohon′ko引理的差分模拟; 慢增长亚纯函数的差分、均差分的零点和不动点的性质; 差分多项式的值分布性质;差分Riccati方程与差分Painlevé方程亚纯解的性质;复域q-差分及q-差分方程的解析性质.
复域差分; 差分方程; 复域q-差分;q-差分方程; 亚纯函数值分布
1925年,NEVANLINNA[1]发表了关于亚纯函数理论的论文,后来发展为亚纯函数Nevanlinna理论.随后, 亚纯函数Nevanlinna理论被运用到线性和非线性微分方程亚纯解的值分布、唯一性和存在性等问题的讨论, 获得丰富的成果[2-8].
然而,利用亚纯函数Nevanlinna理论,对差分方程的研究可以追溯到二十世纪初期[9-10].由于缺乏有力的研究工具,复域差分方程理论的发展极其缓慢.虽然在20世纪七、八十年代,BANK和KAUFMAN[11], SHIMOMURA[12]和YANAGIHARA[13]获得一些关于差分方程亚纯解存在性的初始结果. 特别地,BANK和KAUFMAN[11]证明了, 对任意关于z的有理函数R(z),差分方程
f(z+1)-f(z)=R(z)
(1)
总存在满足条件T(r,f)=O(r)的亚纯解f(z). YANAGIHARA[13]证明了, 对任意关于f(z)的有理函数R(f(z)),差分方程
f(z+1)=R(f(z))
(2)
有非平凡的亚纯解.
2000年, ABLOWITZ等[14]利用亚纯函数Nevanlinna 理论研究二阶非线性差分方程的可积性问题, 标志着亚纯函数Nevanlinna 理论作用到复域差分方程研究的真正实现. 随后,经过许多复分析和数学物理领域的专家和学者近十几年的努力, 亚纯函数Nevanlinna 理论的差分模拟的研究取得重大突破,从而为复域差分方程的研究提供了有力的理论工具. 由此,复域差分、q-差分、复域差分方程及q-差分方程的研究,以及与之对应的唯一性理论的差分模拟的研究,逐渐成为热门研究课题.
近十年来,亚纯函数Nevanlinna理论为复域差分、q-差分、复域差分方程及q-差分方程的研究和发展提供了一个有力的工具,主要体现在亚纯函数的对数导数引理的差分模拟和Clunie-Mohon′ko引理的差分模拟. 下面将介绍其差分形式和q-差分形式.


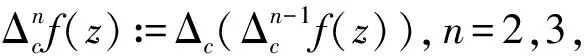
有限级亚纯函数的对数导数引理的差分模拟, 是由CHIANG和FENG[15]、HALBURD和KORHONEN[16-17]分别建立的. 这里, 我们给出它的最终形式.

对所有的r成立,至多除去一个对数测度为有限的集合.
对于有限级亚纯函数f(z)的差分算子, HALBURD和KORHONEN[17]得到如下的对数导数引理.

对所有的r成立, 至多除去一个对数测度为有限的集合.
如果f(z)为无穷级的亚纯函数, HALBURD等[18]和KORHONEN[19]获得对数导数引理的差分模拟的更一般的形式.

对所有的r成立,至多除去一个集合E满足
如果f(z)的超级σ2(f)<1和ε>0,那么
对所有的r成立, 至多除去一个对数测度为有限的集合.
定理4[19]设f(z)为非常数亚纯函数,ω(z)=czn+pn-1zn-1+…+p0和φ(z)=czn+qn-1zn-1+…+q0是2个非常数多项式. 如果
那么
对所有的r成立,至多除去一个对数测度为有限的集合.
Clunie引理和Mohon′ko引理在微分多项式的值分布和微分方程亚纯解的增长级估计方面具有重要的作用.Clunie 引理的差分模拟最初形式可以参考文献[16]的定理3.1和文献[20]的定理2.3,对于更进一步的结果, 可以参考文献[21]-[23]. 下面给出其最初结论.
定理5 设f(z)是增长级为σ(<∞)的亚纯函数,且满足方程
U(z,f)P(z,f)=Q(z,f),
其中U(z,f),P(z,f)和Q(z,f)是差分多项式满足degfQ(z,f)≤degfU(z,f)=n. 更进一步地,U(z,f)仅含一项次数最大的项. 那么,对任意ε>0,
m(P(z,f))=O(rσ-1+ε)+S(r,f)
对所有的r成立, 至多除去一个对数测度为有限的集合.
下面给出Mohon′ko引理的差分模拟.
定理6[16,20]设f(z)是有限级亚纯函数,且满足方程P(z,f)=0,其中P(z,f)是差分多项式.对给定的小函数a(z),如果P(z,a(z))≢0, 那么
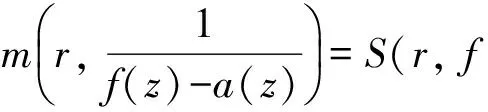


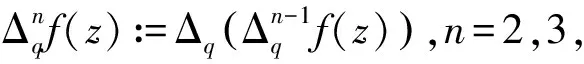
下面将给出对数导数引理、Clunie引理和Mohon′ko引理的q-差分模拟.

在一对数密度为1的集合上成立.
定理8[24]设f(z)是非常数零级亚纯函数且满足fn(z)P(z,f)=Q(z,f),其中P(z,f)和Q(z,f)是关于f(z)的q-差分多项式且degfQ(z,f)≤n,那么
m(r,P(z,f))=o(T(r,f))
在一对数密度为1的集合上成立.
定理9[24]设f(z)是非常数零级亚纯函数且满足P(z,f)=0,其中P(z,f)是关于f(z)的q-差分多项式.对给定的小函数a(z),如果P(z,a(z))≢0, 那么
在一对数密度为1的集合上成立.
对于亚纯函数f(z),其位移f(z+c)和q-位移f(qz)的特征函数等的估计[15,25]、Nevanlinna第二基本定理[17,24]、Wiman-Valiron方法的差分模拟[26]等,这里不再阐述. 基于上述理论的建立,复域差分、q-差分、差分方程及q-差分方程和唯一性理论的差分模拟取得丰富的研究成果.
1 复域差分多项式
鉴于对数导数引理和Clunie-Mohon′ko引理等差分模拟的建立,对复域差分多项式的解析性质的研究,主要体现在差分多项式的值分布和唯一性两方面.
1.1复域差分多项式的值分布


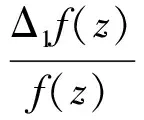
具有无穷多个零点.
同时提出了如下猜想:
猜想1[27]假设f(z)是超越整函数且满足σ(f)<1,那么G(z)有无穷多个零点.
若所考虑的函数f(z)为亚纯函数,BERGWEILER和LANGLEY还证明了:

随后,LANGLEY[28]、CHEN和SHON[29]推广了上述结果,并给出很多新颖的证明方法.特别地,CHEN和SHON[29]首次研究了具有慢增长性级的亚纯函数的差分和均差分的不动点问题, 从而部分地证明了上述猜想.

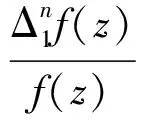
具有无穷多个零点和无穷多个不动点.

(i)至多有有限个极点zj,zk满足zj-zk=c;
那么
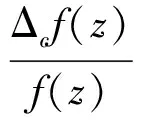
具有无穷多个零点和无穷多个不动点.
对于差分多项式的值分布的研究, 要归结于对HAYMAN[30]所探究的微分多项式值分布的差分模拟[31-33]. 随后, 亚纯函数的差分多项式的值分布获得一系列有趣的结果[23,33-42]. 下面介绍HAYMAN关于微分多项式的几个经典结果的差分模拟.


例1[32]设f(z)=ez+1,则
H(z)=f(z)f(z+iπ)-1=(1+ez)(1-ez)-1=-e2z.
这个例子说明,定理14和定理15中的条件n≥2不能省略. 因此,CHEN等进一步获得如下结果.

1.2复域差分多项式的唯一性
设f(z)和g(z)为2个非常数的亚纯函数,a为任意复数. 如果f(z)-a和g(z)-a具有相同的零点(计算重数), 则称f(z)和g(z)具有CM分担a. 如果f(z)-a和g(z)-a具有相同的零点(不计算重数),则称f(z)和g(z)具有IM分担a. 亚纯函数唯一性理论的典型结果是Nevanlinna五值定理和四值定理[8]. 亚纯函数唯一性理论的已有文献指出,对于任意2个亚纯函数, 如果其分担值的个数减少, 需要增加额外的假设.基于这一事实,HEITTOKANGAS等[43-44]首先研究了亚纯函数f(z)和它的位移算子f(z+c)的唯一性,后来进一步提升已有的结果, 得到



近几年来, 很多学者在这一方面做出很多有意义的结果[42,45-54].
关于亚纯函数唯一性理论的差分模拟, Brück猜想[55]的差分模拟具有重要的地位. 下面介绍几个经典的结果,更多的结果可参考文献[33]、[44]、[48]-[49]、[56].


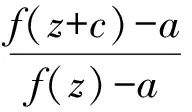

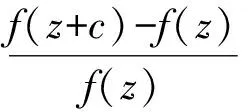
其中A为一非零常数.
2 复域差分方程
复域微分方程的复振荡理论在过去30多年发展迅速, 获得一系列的成果[2,5-6].这些成果揭示了微分方程亚纯解的增长级和其系数增长级之间的关系,刻画了微分方程亚纯解的零点、 极点和不动点等性质. 近十年来,随着亚纯函数Nevanlinna理论的差分模拟的建立,对函数差分方程亚纯解性质的研究, 也进入一个繁荣时期.
2.1复域差分方程
ABLOWITZ等[14]考虑复域离散方程作为复域时滞方程,运用亚纯函数Nevanlinna理论对其研究,为复域差分方程的研究提供了有力的工具.随后,HALBURD和KORHONEN[57]利用奇异测试的方法证明了:如果二阶差分方程
f(z+1)+f(z-1)=R(z,f)
(3)
存在有限级亚纯解f(z),那么f(z)或者满足差分Riccati方程
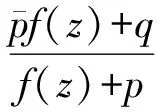
或者可经过一线性变换,将方程(3)转化为一些典型的线性差分方程和差分Painlevé方程.
2.1.1 复域差分方程亚纯解的存在性 对复域差分方程亚纯解存在性的研究,主要体现在有理解的存在性及其表示[58-61]、渐近解的存在性[57,61-62]和亚纯解的表示[15,63-66]. 下面列出一些典型结果.
定理21[58]设a,b,c是常数且a,b不全为零.
(i)如果a≠0,那么差分Painlevé I方程
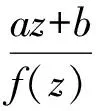
(4)
没有有理解;
(ii)如果a=0和b≠0,那么差分Painlevé I方程(4)有一个非零常数解f(z)=A满足
2A2-cA-b=0,
其他有理解具有形式f(z)=P(z)/Q(z),其中P(z)和Q(z)是互素的多项式且其次数满足degP 定理22[59]设δ=±1,A(z)=m(z)/n(z)是不可约的有理函数,其中m(z)和n(z)是多项式,其次数分别为degm(z)=m和degn(z)=n. (i)假设m≥n且m-n是偶数或零.如果差分Riccati方程 (5) 有一个不可约的有理解f(z)=P(z)/Q(z),其中P(z)和Q(z)是多项式且其系数分别为degP(z)=p和degQ(z)=q, 那么p-q=(m-n)/2; (ii)假设m≤n且m-n=k(≥2)是一正整数.如果差分Riccati方程(5)有一个不可约的有理解f(z)=P(z)/Q(z),那么q-p=k-1或q-p=1; (iii)假设m>n且m-n是奇数,或m SHIMOMURA[61]考虑差分Painlevé方程 (6) (7) (8) (9) 定理23[61]如果α≠0,那么差分方程(6)~(8)没有有理解. 对于一阶非线性差分方程 f(z+1)=R(f(z)), (10) 其中R(f(z))是关于f(z)的常系数有理函数,HALBURD和KORHONEN[62]获得方程(10)非平凡亚纯解满足一定的渐近性质. (f(z)-γ)λ-z→α, Rez→-∞. 对于差分方程亚纯解的表示形式,ISHIZAKI[63]获得差分Riccati方程亚纯解的表示性质. 定理26[63]设A(z)为一亚纯函数.如果差分Riccati方程 (11) 存在3个不同的亚纯解f1(z)、f2(z)和f3(z), 那么方程(11)的任一亚纯解f(z)可以表示为 f(z)= (12) 其中Q(z)是周期为1的亚纯函数. 反之,对于任意周期为1的亚纯函数, 我们定义函数f(z)具有式(12)的形式,那么f(z)是方程(11)的亚纯解. 2.1.2 复域差分方程亚纯解的值分布 对于差分方程(包括:一般的差分方程、差分Painlevé方程和差分Riccati方程)亚纯解的值分布,主要体现在差分方程亚纯解的增长级、零点收敛指数、极点收敛指数、不动点收敛指数和Borel例外值的存在性, 详见文献[11]、[15]、[20]、[57]-[60]、[62]、[64]-[71]等, 这里不再赘述. 2.2复域函数方程 复域q-差分方程(函数方程)的研究可追溯到RITT[72]研究的自治Schröder方程f(qz)=R(f(z)),其中R(f(z))是关于f(z)的常系数有理函数,和VALIRON[73]研究的非自治Schröder方程f(qz)=R(z,f(z)),其中R(z,f(z))是关于z、f(z)的有理函数,它们是与复动力系统紧密联系的方程[73-76]. 2.2.1 复域q-差分方程亚纯解的存在性 具有有理系数的线性q-差分方程(函数方程), 其亚纯解不一定存在. 近十年来,BEIGWEILER、GUNDERSEN和HEITTOKANGAS等[77-79]在一定的系数约束下,研究了q-差分方程亚纯解的存在性.下面给出一些经典结果. 定理27[78]设f(z)是q-差分方程 f(qz)=A(z)+γf(z)+δf(z)2, (13) (i)在方程(13)中,如果 那么方程(13)有2个不同的亚纯解; (ii)在方程(13)中, 如果(1-γ)2=4,那么方程(13)只有一个亚纯解. 定理28[79]设a0(z),a1(z),…,an(z)是复常数满足 和Q(z)=g1(z)是一整函数.那么q-差分方程 (14) 只有唯一的整函数解. 定理29[77]考虑q-差分方程 f(q2z)+a(z)f(qz)+b(z)f(z)=0, (15) (i)如果不存在整数n满足q2n+a0qn+b0=0, 那么方程(15)没有任何超越亚纯解; (ii)如果b0≠0且存在整数n满足q2n+a0qn+b0=0,那么方程(15)存在一个超越亚纯解; (iii)如果b0=0,那么方程(15)没有任何超越亚纯解. 对于q-差分方程亚纯解的表示形式,HUANG[80]获得q-差分Riccati方程亚纯解的表示性质: (16) 存在3个不同的亚纯解g1(z)、g2(z)和g3(z),那么方程(16)的任一亚纯解f(z)可以表示为 g(z)= (17) 其中φ(z)是亚纯函数且满足φ(qz)=φ(z).反之,对于任意亚纯函数φ(z)且满足φ(qz)=φ(z),我们定义函数f(z)具有式(17)的形式,那么f(z)是方程(16)的亚纯解. 2.2.2 复域q-差分方程亚纯解的值分布 随着亚纯函数q-差分模拟的建立,q-差分方程亚纯解的值分布性质也得到广泛探讨, 详见文献[47]、[77]-[86]等, 这里不再赘述. 亚纯函数Nevanlinna理论差分模拟的建立,为复域(q-)差分多项式和复域(q-)差分方程的发展开辟了新天地.但由于对复域差分方程的研究,没有普适的研究方法,针对不同形式的差分方程,我们需要寻求其特有的解法,特别是差分方程亚纯解的存在性方面,还有大量的工作需要去探讨. [1] NEVANLINNA R. Zur theorie der meromorphen funktionen (German)[J].Acta math,1925,46(1-2):1-99. [2] GAO S A,CHEN Z X,CHEN T W. Complex oscillation theory of linear differential equations[M].Wuhan: Huazhong Univ Sci Tech Press, 1998. [3] GROMAK V,LAINE I,SHIMOMURA S.Painlevé differential equations in the complex plane[M].Berlin-New York:Walter de Gruyter,2002. [4] HAYMAN W K. Meromorphic functions[M].Oxford:Clarendon Press,1964. [5] HILLE E.Ordinary differential equations in the complex domain[M].Mineola, NY:Dover Publications, Inc,1997. [6] LAINE I. Nevanlinna theory and complex differential equations[M].Berlin:Walter de Gruyter,1993. [7] YANG L.Value distribution theorem and new research[M]. Beijing: Science Press, 1982. [8] YANG C C,YI H X. Uniqueness theory of meromorphic functions[M]. Dordrecht: Kluwer Academic Publishers Group, 2003. [9] BIRKHOFF G D.General theory of linear difference equations[J].Trans Amer Math Soc,1911,12(2):243-283. [10] CARMICHAEL R D.Linear difference equations and their anaytic solutions[J].Trans Amer Math Soc,1911,12(1):99-134. [11] BANK S B,KAUFMAN R P. An extension of Hölder′s theorem concerning the gamma function[J]. Funkcial Ekvac, 1976,19(1):53-63. [12] SHIMOMURA S. Entire solutions of a polynomial difference equation[J].J Fac Sci Uni Tokyo Sect IA Math,1981,28(2):253-266. [13] YANAGIHARA N. Meromorphic solutions of some difference equations[J].Funkcial Ekvac,1980,23(2):309-326. [14] ABLOWITZ M J,HALBURD R,HERBST B. On the extension of the Painlevé property to difference equations[J]. Nonlinearity, 2000, 13(3):889-905. [15] CHIANG Y M,FENG S J. On the Nevanlinna characteristic of and difference equations in the complex plane[J]. Ramanujan J,2008,16(1):105-129. [16] HALBURD R G,KORHONEN R J. Difference analogue of the lemma on the logarithmic derivative with applications to difference equations[J].J Math Anal Appl,2006,314(2):477-487. [17] HALBURD R G,KORHONEN R J. Nevanlinna theory for the difference operator[J]. Ann Acad Sci Fenn Math,2006,31(2):463-478. [18] HALBURD R G,KORHONEN R J,TOGHN K.Holomorphic curves with shift invariant hyperplane preimages[J].arXiv:0903.3236. [19] KORHONEN R.An extension of Picard′s theorem for meromorphic functions of small hyper order[J].J Math Anal Appl,2009,357(1):244-253. [20] LAINE I,YANG C C. Clunie theorems for difference and q-difference equations[J].J London Math Soc,2007,76(3):556-566. [21] HUANG Z B,CHEN Z X. A Clunie lemma for difference and q-difference polynomials[J].Bull Aust Math Soc,2010,81(1):23-32. [22] KORHONEN R. A new Clunie type theorem for difference polynomials[J].J Difference Equ Appl,2011,17(3):387-400. [23] ZHANG R R,CHEN Z X. Value distribution of difference polynomials of meromorphic functions[J]. Sci China:Ser A,2012, 42(11):1115-1130. [24] BARNETT D C,HALBURD R G,MORGAN W,et al. Nevanlinna theory for the q-difference operator and meromorphic solutions of q-difference equations[J].Proc Roy Soc Edinburgh:Sec A,2007,137(3):457-474. [25] ZHANG J L,KORHONEN R. On the Nevanlinna characteristic off(qz) and its applications[J].J Math Anal Appl,2010,369(2):537-544. [26] ISHIZAKI K,YANAGIIHARA N.Wiman-Valiron method for difference equations[J].Nagoya Math J,2004,175:75-102. [27] BERGWEILER W,LANGLEY J K.Zeros of meromorphic functions[J].Math Proc Camb Phil Soc,2007,142(1):133-147. [28] LANGLEY J K. Value distribution of difference of meromorphic functions[J].Rocky Mountain J Math,2011,41(1):275-291. [29] CHEN Z X,SHON K H. On zeros and fixed points of differences of meromorphic functions[J]. J Math Anal Appl, 2008, 344(1):373-383. [30] HAYMAN W K.Picard values of meromorphic functions and their derivatives[J].Ann Math,1959,70(2):9-42. [31] CHEN Z X,HUANG Z B,ZHENG X M. On properties of difference polynomials[J].Acta Math Sci:Ser B,2011,31(2):627-633. [32] LAINE I,YANG C C.Value distribution of difference polynomials[J].Proc Japan Acad:Ser A,2007,83(8):148-151. [33] LIU K,YANG L Z. Value distribution of their difference operator[J].Arch Math,2009,92(3):270-278. [34] CHEN Z X. On value distribution of difference polynomials of meromorphic functions[J]. Abstr Appl Anal,2011,Art.ID 239853, 9pp. [35] CHEN Z X,SHON K H.Properties of differences of meromorphic functions[J].Czechoslovak Math J,2011,61(1):213-224. [36] CHEN Z X. Value distribution of products of meromorphic functions and their differences[J]. Taiwanese J Math,2011,15(4):1411-1421. [37] CHEN Z X,SHON K H. Estimates for the zeros of difference of meromorphic functions[J]. Sci China:Ser A, 2009, 52(11):2447-2458. [38] LIU K,LAINE I. A note on value distribution of difference polynomials[J]. Bull Aust Math Soc,2010,81(3):353-360. [39] LIU Y,YI H X. On zeros of differences of meromorphic functions[J]. Ann Polon Math,2011,100(2):167-178. [40] LIU Y,YI H X. On growth and zeros of difference of some meromorphic funtions[J].Ann Polon Math,2013,108(3):305-318. [41] ZHANG R R,CHEN Z X.Value distribution of meromorphic functions and their differences[J].Turkish J Math,2012,36(2):395-406. [42] ZHANG J L.Value distribution and shared set of differences of meromorphic functions[J].J Math Anal Appl,2010,367(2):401-408. [43] HEITTOKANGAS J,KORHONEN R,LAINE I,et al.Uniqueness of meromorphic functions sharing values with their shifts[J]. Complex Var Elliptic Equ,2011,56(1-4):81-92. [44] HEITTOKANGAS J,KORHONEN R,LAINE I,et al.Value sharing results for shifts of meromorphic functions, and sufficient condition for periodicity[J].J Math Anal Appl,2009,355(1):352-363. [45] CHEN B Q,CHEN Z X.Meromorphic function sharing two sets with itts difference operator[J]. B Malays Math Sci So,2012,35(3):765-774. [46] CHEN B Q,CHEN Z X,LI S.Uniqueness of difference operators of meromorphic functions[J]. J Inequal Appl,2012,48:1-9. [47] HUANG Z B. Value distribution and uniqueness on q-differences of meromorphic functions[J].Bull Korean Math Soc,2013,50(4):1157-1171. [48] LI S,GAO Z S. A note on the Brück conjecture[J]. Arch Math,2010,95(3):257-268. [49] LI X M,KANG C Y,YI H X. Uniqueness theorems of entire functions sharing a nonzero complex number with their difference operators[J]. Arch Math,2011,96(6):577-587. [50] LI X M,YI H X,KANG C Y. Notes on entire functions sharing an entire function of a small order with their difference operators[J]. Arch Math,2012,99(3):261-270. [51] LUO X D,LIN W C.Value sharing results for shifts of meromorphic functions[J]. J Math Anal Appl,2011,377(2):441-449. [52] QI X G,YANG L Z,LIU K. Uniqueness and periodicity of meromorphic functions concerning the difference operator[J].Computers and Math Appl,2010,60(6):1739-1746. [53] QI X G,LIU K,YANG L Z. Value sharing results of a meromorphic functionf(z) andf(qz)[J]. Bull Korean Math Soc,2011,48(6):1235-1243. [54] QI X G,LIU K.Uniqueness and value distribution of differences of entire funtions[J]. J Math Anal Appl,2011,379(1):180-187. [55] BRÜCK R. On entire functions which share one value CM with their first derivate[J]. Results Math,1996,30(1-2):21-24. [56] CHEN Z X,YI H X. On sharing values of meromorphic functions and their differences[J].Results Math,2013,63(1-2):557-565. [57] HALBURD R G,KORHONEN R J. Finite-order meromorphic solutions and the discrete Painlevé equations[J].Proc Lond Math Soc,2007,94(2):443-474. [58] CHEN Z X,SHON K H.Value distribution of meromorphic solutions of certain difference Painlevé equations[J].J Math Anal Appl,2010,364(2):556-566. [59] CHEN Z X,SHON K H.Some results on difference Riccati equations[J]. Acta Math Sin,2011, 27(6):1091-1100. [60] CHEN Z X,HUANG Z B,ZHANG R R. On difference equations relating to gamma function[J]. Acta Math Sci:Ser B, 2011,31(4):1377-1382. [61] SHIMOMURA S. Rational solutions of difference Painleve equations[J]. Tokyo J Math,2012,35(1):85-95. [62] HALBURD R G,KORHONEN R J. Existence of finite order meromorphic solutions as a detector of integrability in difference equations[J]. Phys D,2006,218(2):191-203. [63] ISHIZAKI K. On difference Riccati equations and second order linear difference equations[J]. Aequationes Math,2011,81(1-2):185-198. [64] PANG C W,CHEN Z X. On a conjecture concernng some nonlinear difference equations[J].Bull Malays Math Sci Soc,2013,35(2):765-774. [65] YANG C C,LAINE I. On analogies between nonlinear difference and differential equations[J]. Proc Japan Acad:Ser A,2010,86(1):10-14. [66] ZHANG J,LIAO L W. On entire solutions of a certain type of nonlinear differential and difference equations[J]. Taiwanese J Math,2011,15(5):2145-2157. [67] CHEN Z X.Growth and zeros of meromorphic solution of some linear difference equations[J]. J Math Anal Appl, 2011,373(1):235-241. [68] HEITTOKANGAS J,KORHONEN R,LAINE I,et al.Complex difference equations of Malmquist type[J].Comput Methods Funct Theory,2001,1(1):27-39. [69] LAINE I,RIEPPO J,SILVENNOINEN H. Remarks on complex difference equations[J].Comput Methods Funct Theory,2005, 5(1):77-88. [70] WANG J. Growth and poles of meromorphic solutions of some difference equations[J].J Math Anal Appl,2011,379(1):367-377. [71] ZHENG X M,CHEN Z X,TU J. Growth of meromorphic solutions of some difference equations[J]. Appl Anal Discrete Math,2010,4(2):309-321. [72] RITT J F.Transcendental transcendency of certain functions of Poincaré[J].Math Ann,1926,95(1):671-682. [73] VALIRON G. Fonctons analytiques[M]. Paris:Univ de France, 1954. [74] ISHIZAKI K,YANAGIIHARA N. Borel and Julia directions of meromorphic Schröder functions[J]. Math Proc Combridge Philos Soc,2005,139(1):139-147. [75] ISHIZAKI K,YANAGIIHARA N.Deficiency for meromorphic solutions of Schröder equations[J]. Complex Var Theory Appl,2004,49(7-9):539-548. [76] ISHIZAKI K,YANAGIIHARA N. Singular directions of meromorphic solutions of some non-autonomous Schröder equations[J].Adv Stu Pure Math, 2006,44:155-166. [77] BERGWEILER W,ISHIZAKI K,YANAGIHARA N. Meromorphic solutions of some functional equations[J]. Methods Appl Anal,1998,5(3):248-258.Erratum: Methods Appl Anal,1999, 6(4): 617-618. [78] GUNDERSEN G G,HEITTOKANGAS J,LAINE I,et al.Meromorphic solutions of generalized Schröder equations[J].Aequationes Math,2002,63(1-2):110-135. [79] HEITTOKANGAS J,LAINE I,RIEPPO J,et al.Meromorphic solutions of some linear functional equations[J]. Aequationes Math,2000,60(1-2):148-166. [80] HUANG Z B. On q-difference Riccati equations and second-order linear q-difference equations[J].J Complex Anal, 2013: Art 938579, 10 pp. [81] BERGWEILER W,ISHIZAKI K,YANAGIHARA N.Growth of meromorphic solutions of some functional equations I[J]. Aequationes Math, 2002,63(1-2):140-151. [82] CHEN B Q,CHEN Z X,LI S. Properties on solutions of some q-difference equations[J]. Acta Math Sin, 2010, 26(10):1877-1886. [83] CHEN B Q,CHEN Z X.Meromorphic solutions of some q-difference equations[J]. Bull Korean Math,2011,48(6):1303-1314. [84] LIU K,QI X G. Meromorphic solutions of q-shift difference equations[J]. Ann Polon Math,2011,101(3):215-225. [85] ZHENG X M,CHEN Z X. Some properties of meromorphic solutions of q-difference equations[J].J Math Anal Appl,2010,361(2):472-480. [86] ZHENG X M,CHEN Z X. Value distribution of meromorphic solutions of some q-difference equations[J]. J Math Res Exposition, 2011,31(4):698-704. Keywords: complex difference; difference equations; complexq-difference;q-difference equations; value distribution of meromorphic functions StudyonComplexDifferencesandDifferenceEquations CHEN Zongxuan*, HUANG Zhibo (School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China) The researches on the complex difference, complexq-difference, difference equations andq-difference equations in recent decades are mainly introduced. These results include the difference analogue of the logarithmic derivative; the difference analogue of Clunie lemma; the difference counterpart of Mohon′ko lemma; the properties on the zeros, fixed-points on complex differences and divided difference of meromorphic functions with small order; the properties on the value distribution of difference polynomials, the properties on the meromorphic solutions of difference Riccati and Painlevé equations; the results onq-differences and meromorphic solutions ofq-difference equations. 2013-07-04 国家自然科学基金项目(11171119) *通讯作者:陈宗煊,教授,Email:chzx@vip.sina.com. 1000-5463(2013)06-0026-08 O174.5 A 10.6054/j.jscnun.2013.09.004 【中文责编:庄晓琼 英文责编:肖菁】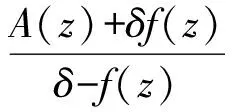
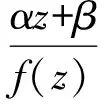



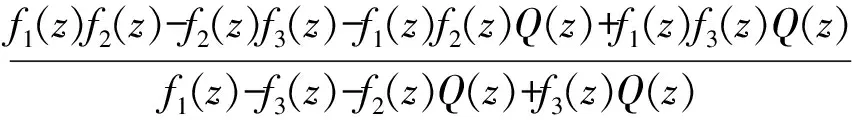





3 结束语

