两族渐近非扩张映射隐迭代序列收敛定理

宋传静， 吴健荣

(苏州科技学院数理学院，江苏苏州 215011)

两族渐近非扩张映射隐迭代序列收敛定理

宋传静， 吴健荣*

(苏州科技学院数理学院，江苏苏州 215011)

研究一致凸Banach空间中两族渐近非扩张映射的公共不动点逼近问题.构造关于两族渐近非扩张映射的隐迭代序列，并在适当条件下，证明了该序列收敛到公共不动点的一些强弱收敛定理.

一致凸Banach空间； 渐近非扩张映射； 隐迭代序列； 公共不动点

本文假设E是一实Banach空间，D是E的非空子集,T:D→D是一个映射，记T的不动点集合为F(T).

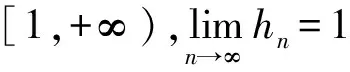
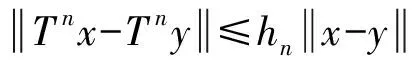
GOEBEL等[1]在1972年引进了渐近非扩张映射，并证明如果D是实一致凸Banach空间E的非空闭凸子集，T是D上的渐近非扩张映射，则T在D中有不动点.

渐近非扩张映射的研究已取得了一定的成果[2-8].尤其是CHANG[7]研究了一族渐近非扩张映射的带误差的隐迭代序列，具体如下.

x1=α1x0+(1-α1)T1x1+u1,

x2=α2x1+(1-α2)T2x2+u2,

…

xN=αNxN-1+(1-αN)TNxN+uN,

…

…

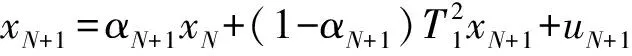
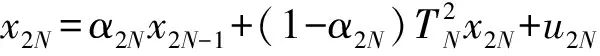
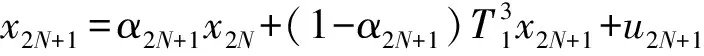
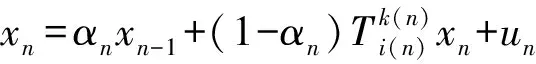
其中，按如下形式

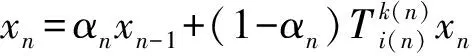
(1)

定义的迭代序列{xn}⊂D称为一族渐近非扩张映射{T1,T2,…,TN}的隐迭代序列.并且关于上述2个序列的强弱收敛定理在文献[7]也有所探讨.

本文构造了一个关于两族渐近非扩张映射的隐迭代序列，并证明了该序列的一些强弱收敛定理.

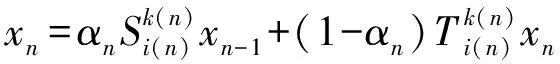
(2)

其中，n,k(n),i(n)与在式(1)中的意义相同.

1 预备知识

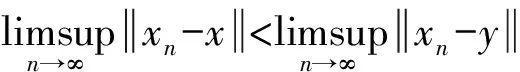
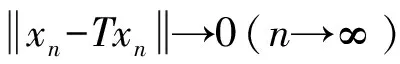
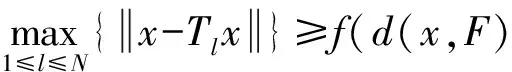
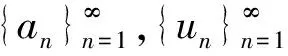
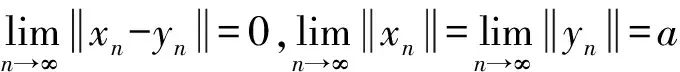
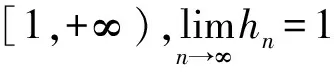
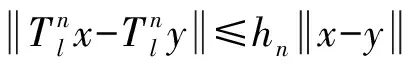
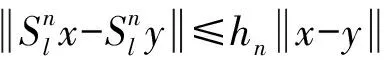
2 主要结果

首先，证明下面的引理.

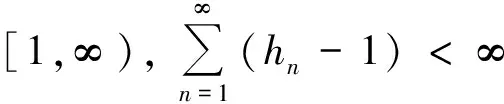
(3)

因此

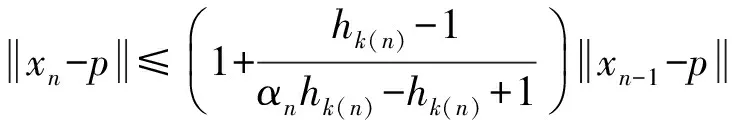
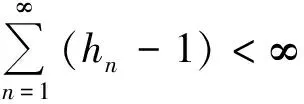
αnhk(n)-hk(n)+1=αn(1+μk(n))-μk(n)=

αn-(1-αn)μk(n)≥δ-(1-δ)μk(n)≥

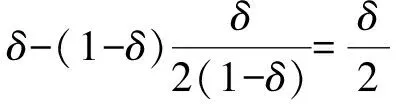
因此

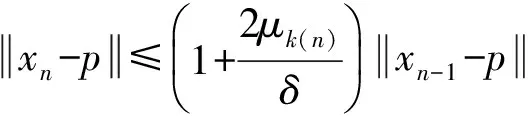
引理5 在引理4的假设下,如果有

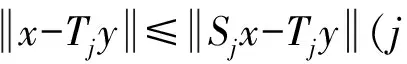
则

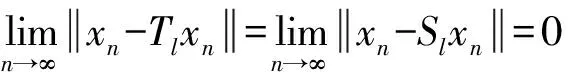
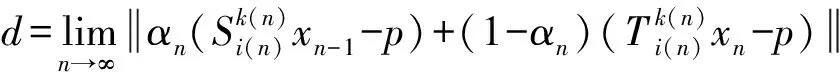
又

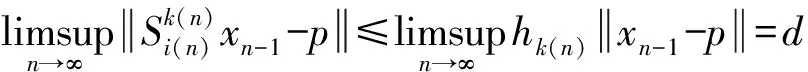
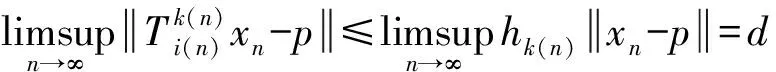
故由引理2可得

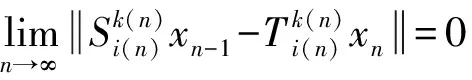
(4)

而又由题设条件得

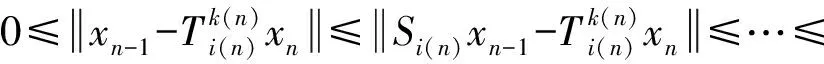
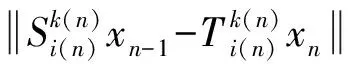
所以由式(4)可得

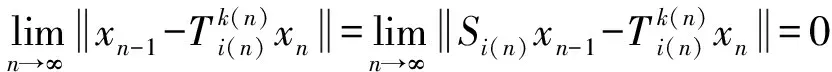
(5)

再由式(4)、(5)和

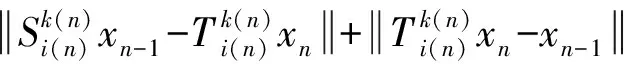
可得

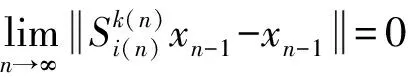
(6)

而由式(5)、(6)和

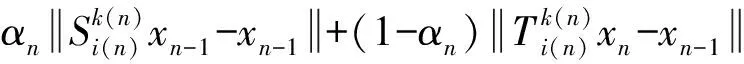
又可得

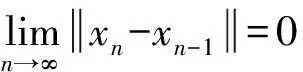
因此

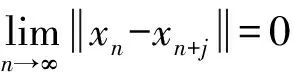
(7)

且由式(5)、(7)和

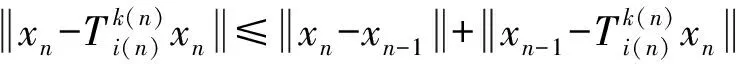
可得

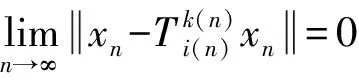
(8)

n-N=((k(n)-1)-1)N+i(n)=

(k(n-N)-1)N+i(n-N),

即

k(n-N)=k(n)-1,i(n-N)=i(n).

又

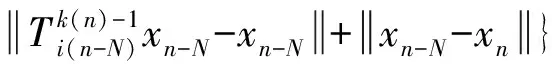
其中

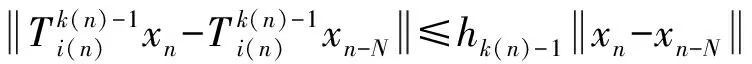
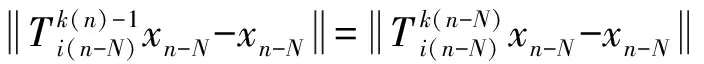
则由式(7)、(8)可得

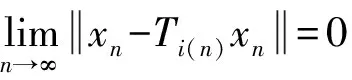
(9)

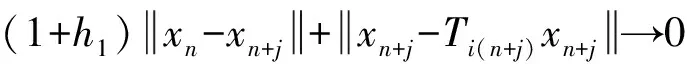
并由此可得

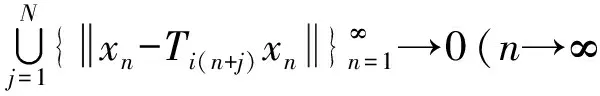
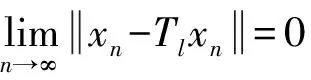
又由式(5)和

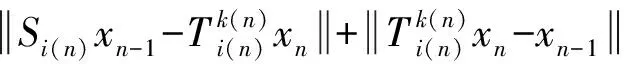
可得

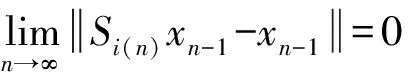
(10)

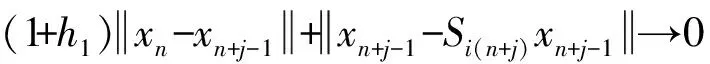
故同理可得

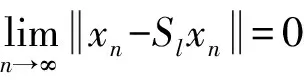
下面证明收敛定理.

定理1 在引理4的假设下，序列{xn}强收敛到{T1,T2,…,TN,S1,S2,…,SN}的公共不动点当且仅当

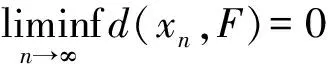
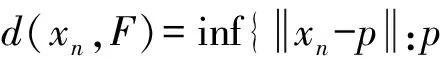
证明必要性显然，下面只证充分性.

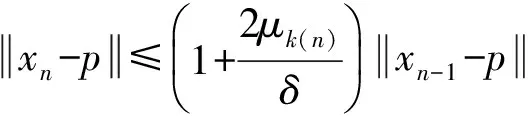
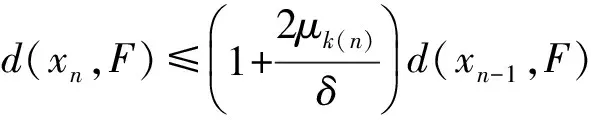
现在证明{xn}是D中的Cauchy列.由

及1+x≤ex(x≥0)可得

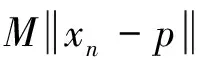
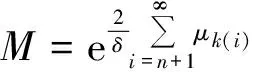
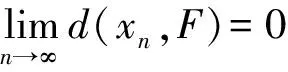
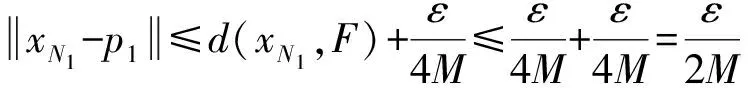
因此，当n≥N1，m≥1时有

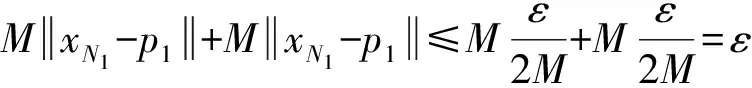
即{xn}是D中的Cauchy列.

证明由引理5知

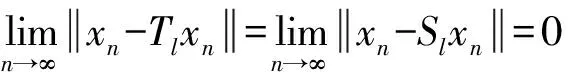
再由题设条件可知

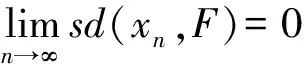
其中s>0为常数.因此由定理1知定理2成立.

定理3 在引理5的假设下，如果{T1,T2,…,TN,S1,S2,…,SN}满足条件(B),则{xn}强收敛到{T1,T2,…,TN,S1,S2,…,SN}的公共不动点.

证明由引理5知

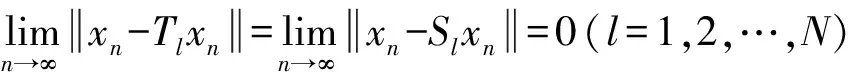
因此

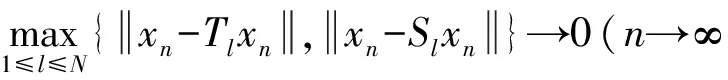
定理4 在引理5的假设下，如果存在一个Tl或Sl(1≤l≤N)是半紧的，则{xn}强收敛到{T1,T2,…,TN,S1,S2,…,SN}的公共不动点.

证明不妨设T1是半紧的，因为{xn}有界且

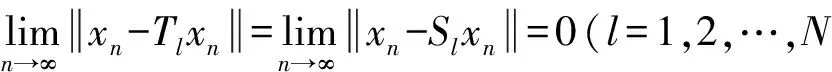
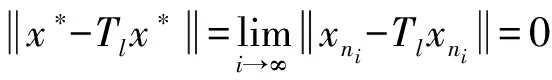
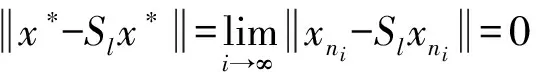
由此可知

故

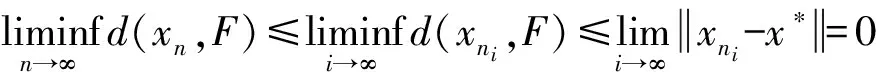
由定理1知定理4成立.

定理5 在引理5的假设下,如果存在一个Tl或Sl(1≤l≤N)是全连续的，则{xn}强收敛到{T1,T2,…,TN,S1,S2,…,SN}的公共不动点.

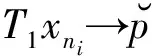
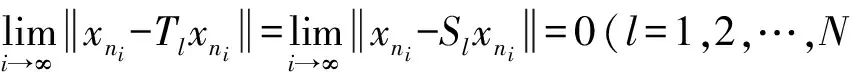
因此当i→∞时，

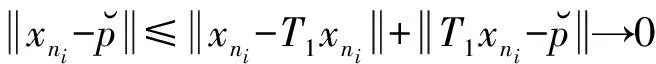
所以有

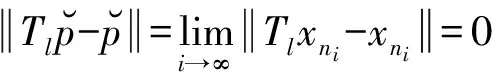
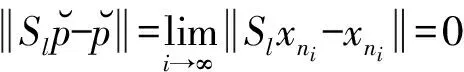
由此即知

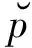
定理6 在引理5的假设下,如果E满足Opial’s条件,则{xn}弱收敛到{T1,T2,…,TN,S1,S2,…,SN}的公共不动点.

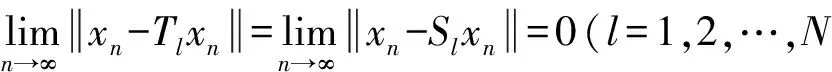
如果p≠p*,那么由题设条件可得

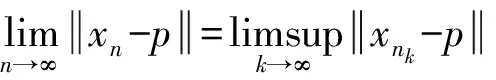
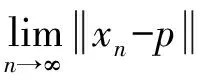
矛盾！因此p=p*.此定理得证.

[1] GOEBEL K, KIRK W A. A fixed point theorem for asymptotically nonexpansive mappings[J]. Proc Amer Math Soc, 1972,35:171-174.

[2] XU B, NOOR M A. Fixed point iterations for asymptotically nonexpansive mappings in Banach space[J]. J Math Anal Appl, 2002,267:444-453.

[3] ZHOU Y Y, CHANG S S. Convergence of implicit iterative process for a fintte family of asymptotically nonexpansive mappings in Banach spaces[J]. Number Funct Anal and Optimiz, 2002,23:911-921.

[4] CHO Y J, ZHOU H, GUO G. Weak and strong convergence theorems for three-step iterations with errors for asymptotically nonexpansive mappings[J]. Comput Math Appl, 2004,47:707-717.

[5] GU Feng. Convergence of implicit iterative process with erroes for a finite family of asymptotically nonexpansive mappings[J]. Acta Math Sci, 2006,26:1131-1143.

[6] CHIDUME C E, ALI B. Weak and strong convergence theorems for finite families of asymptotically nonexpansive mapping in Banach spaces[J]. J Math Anal Appl, 2007,330:377-387.

[7] CHANG S S, TAN K K, LEE H W J. On the convergence of implicit iteration process with error for a finite family of asymptotically nonexpansive mappings[J]. J Math Anal Appl, 2006,313:273-283.

[8] GUO Weiping, CHO Y J. On the strong convergence of the implicit iterative processes with errors for a finite family of asymptotically nonexpansive mappings[J]. Applied Math Letters, 2008,21:1046-1052.

[9] OPIAL Z. Weak convergence of successive approximations for nonexpansive mapping[J]. Bull Amer Math Soc, 1967,73:591-599.

[10] CHIDUME C E, SHAHZAD N. Strong convergence of an implicit iteration process for a finite family of nonexpansive mappings[J]. Nonlinear Analysis, 2005,62:1149-1156.

[11] 李智,崔云安,张新. 渐进拟非扩张映射的三步迭代序列的收敛定理[J].哈尔滨商业大学学报:自然科学版,2009,25(2): 234-236.

[12] SITTHIKUL K, SAEJUNG S. Convergence theorems for a finite family of nonexpansive and asymptotically nonexpansive mappings[J]. Acta Univ Palack Olomu Math Appl, 2009,48:139-152.

Keywords： uniformly convex Banach space； asymptotically nonexpansive mapping； implicit iterative sequence； common fixed point

ConvergenceTheoremsforanImplicitIterationProcessofTwoFiniteFamiliesofAsymptoticallyNonexpansiveMappings

SONG Chuanjing, WU Jianrong*

(School of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou, Jiangsu 215011,China)

The common fixed points of two finite families of asymptotically nonexpansive mappings are studied in real uniformly convex Banach spaces. An implicit iteration process defined by two finite families of asymptotically nonexpansive mappings is introduced. And some strong and weak convergence theorems to a common fixed point for this scheme are proved.

2011-10-14

国家自然科学基金项目(10972151)；江苏省研究生培养创新工程项目(CXZZ11_0950)；苏州科技学院研究生科研创新计划(SKCX11S_054)

*通讯作者:吴健荣，教授，Email:jrwu@mail.usts.edu.cn.

1000-5463(2013)01-0027-05

O177

A

10.6054/j.jscnun.2012.12.005

【中文责编：庄晓琼 英文责编：肖菁】