水平集理论在磁共振脑图像分割中的模型研究
田 丹,吴静飞,范立南
(沈阳大学 信息工程学院,辽宁 沈阳 110044)
在医学图像处理领域,磁共振脑图像分割技术已经成为脑疾病诊断的重要辅助手段.其主要优势在于,脑磁共振成像具有较高的软组织对比度、非侵入性特性和较高的空间分辨率.人脑的软组织大致可以分为几个主要区域,如灰质(GM)、白质(WM)和脑脊液(CSF)等.鲁棒的脑组织分割是一个极具挑战性的任务,因为患者的移动、采集时间的有限性和软组织的边界灰度不均匀性,均会带来大量的数据处理问题.
为了实现鲁棒分割,一些经典方法中引入了形状和灰度分布等先验知识.这些方法主要包括水平集方法[1-3]、神经网络方法[4]和统计法[5]等.其中,水平集方法的基本思想是,在图像区域中指定一个初始轮廓,然后根据速度函数迭代更新该轮廓的形状和位置,使其最终定位到目标边界.由于该方法能提取连续的目标拓扑形状,目前在医学图像分割领域应用很广泛.例如,Chan等人[6]提出了一种著名的基于区域特性的水平集方法,即CV模型.该模型假设图像中的目标和背景区域均具有灰度均匀性.而在实际应用中,数字图像通常存在灰度不均匀性问题,特别是医学图像.例如,由于射频场的不均匀性等因素,导致脑磁共振图像的灰度均匀性变差,表现为同一组织的像素灰度沿空间呈缓慢平滑的变化.为了解决该问题,国内外学者提出了一些改进方法.Li等人[7]提出一种能同时分割和去除偏移场的活动轮廓模型.Tsai等人[8]提出了一种分段光滑模型,但该模型计算量较大,在每次迭代水平集函数时要额外求解两个偏微分方程.本文在CV模型的基础上,引入一种可控的局域算子,使水平集曲线的进化基于图像的局部信息,从而克服了CV模型的图像均匀特性限制.
1 问题描述
1.1 能量准则
假设Ω⊂R2是图像域,I:Ω→R是一个指定的灰度图像.在水平集描述中,由水平集曲线进化形成的进化平面Γ可由零水平集函数φ表示,满足如下关系[9]:
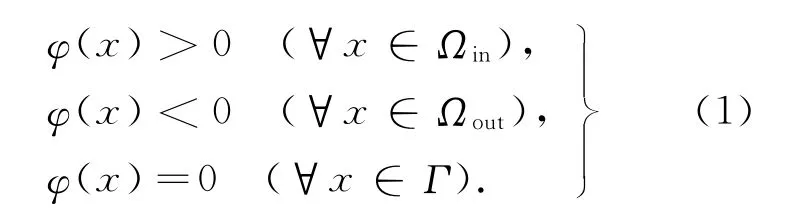
式中,Ωin表示Ω 的内部区域;Ωout可定义为Ω\Ωin,表示Ω的外部区域.
图像分割问题可以通过水平集曲线C的进化实现,这一进化过程等效于指定能量函数的最小化过程,其进化终了的稳定状态对应目标边界.著名的CV模型的能量函数定义如下:
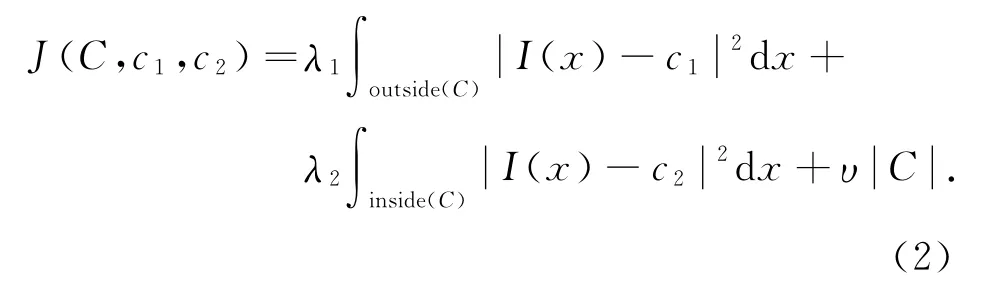
式中,λ1和λ2为正常量;inside(C)和outside(C)分别表示轮廓线C的内部和外部区域;c1和c2分别近似轮廓线外部和内部区域的灰度平均值;|C|代表轮廓线C的长度,是保证曲线平滑的调整项.式(2)中,能量函数的前两项为数据保真项.CV模型的前提条件是假设图像为分段常量,即在每个目标区域内灰度是均匀的.CV模型中能量函数的构建是十分合理的.若曲线C在目标外部,则能量函数的第一项近似于0,而第二项大于0.若曲线C在目标内部,则能量函数的第一项大于0,而第二项近似于0.若曲线C跨越目标的内部和外部区域,则能量函数的前两项均大于0.不难看出,当且仅当曲线C在目标边界上时,能量函数才能达到最小值.
1.2 局域化处理
考虑到磁共振成像脑图像存在灰度不均匀性问题,这时依靠单一的全局灰度均值不能表征图像特征,CV模型将区分不出目标和背景.本文在CV模型基础上,在局域范围内重新描述能量函数,从而使水平集轮廓进化可以基于图像的局域信息.基于局域信息的能量函数定义如下:
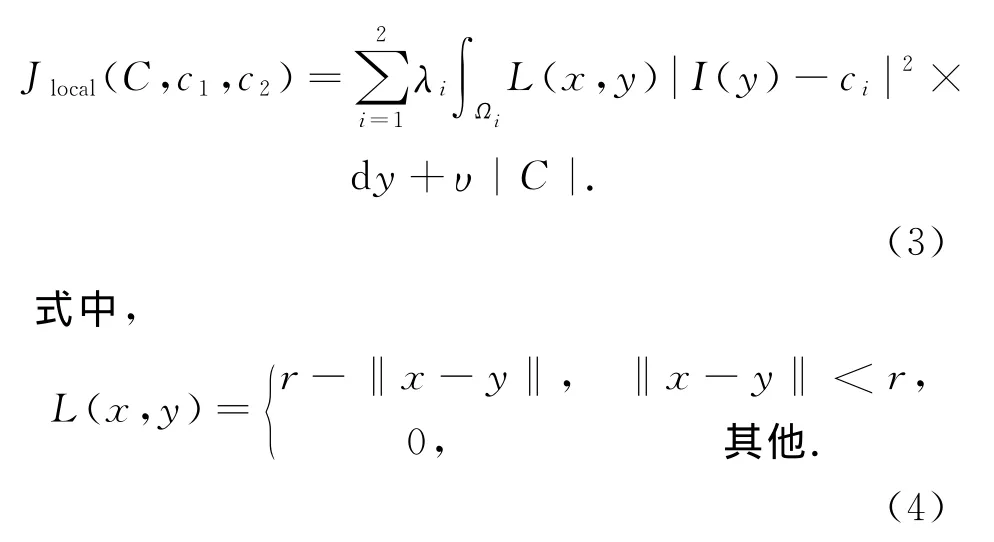
能量函数中引入了一个新的空间变量y,它独立于变量x.换句话说,x和y分别代表Ω内独立的空间点.在函数L(x,y)的约束下,能量函数中的灰度I(y)可以被限制在以点x为中心的局部区域范围内,其局域尺寸可由半径参数r控制.随着点y逐渐远离中心点x,灰度I(y)对能量函数的作用将逐渐递减并趋近于0.该局域区域可以是一个小的邻域,也可以逐步扩展到整个图像区域.
为了获取整个目标边界,能量函数应该在整个图像区域中作最小化处理.这可以通过最小化图像区域中所有中心点x对应的能量函数的积分来实现,定义如下:这里,能量函数的参量设定为水平集曲线C.为了处理拓扑结构的变化,将其转变为水平集模型.
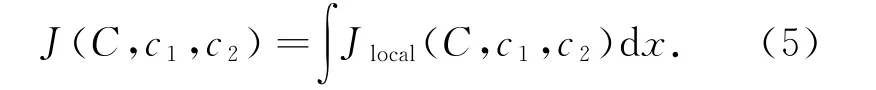
1.3 水平集模型
为了最优化能量函数,进化曲线C可以利用前面提到的零水平集函数φ表示.能量函数可以重新描述为
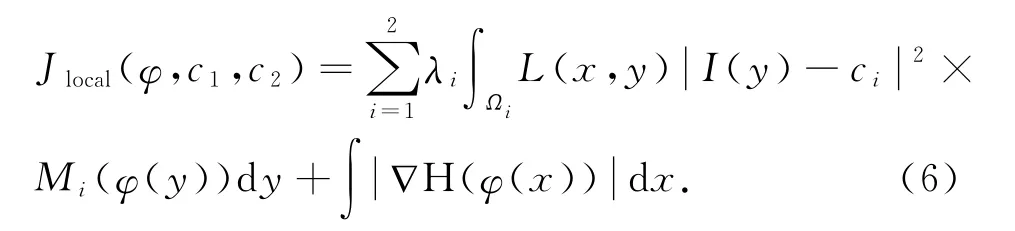
式中,M1(φ)=H(φ),M2(φ)=1-H(φ);H(·)是Heaviside函数,定义为
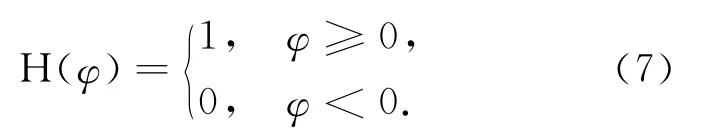
这里,进化曲线的长度由Heaviside函数的积分求出.为了最小化该能量函数,需要满足如下欧拉方程:
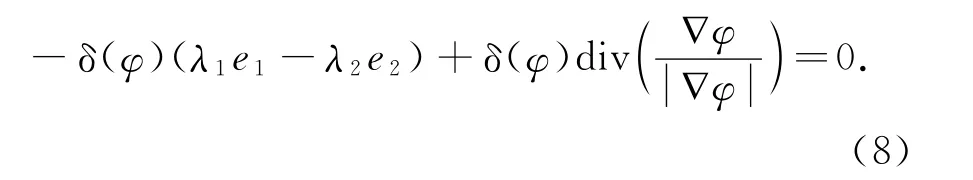
式中,δ(φ)是一维Dirac函数:
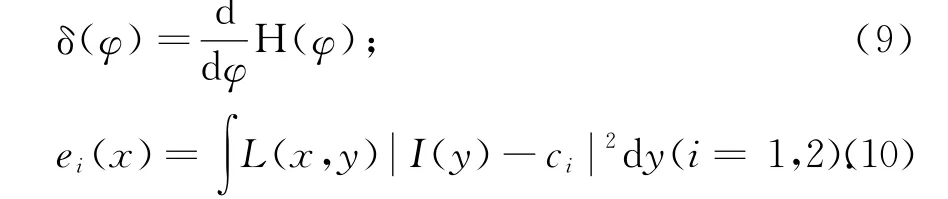
对于一个固定的水平集函数φ,c1和c2分别对应进化曲线外部区域和内部区域的灰度平均值.
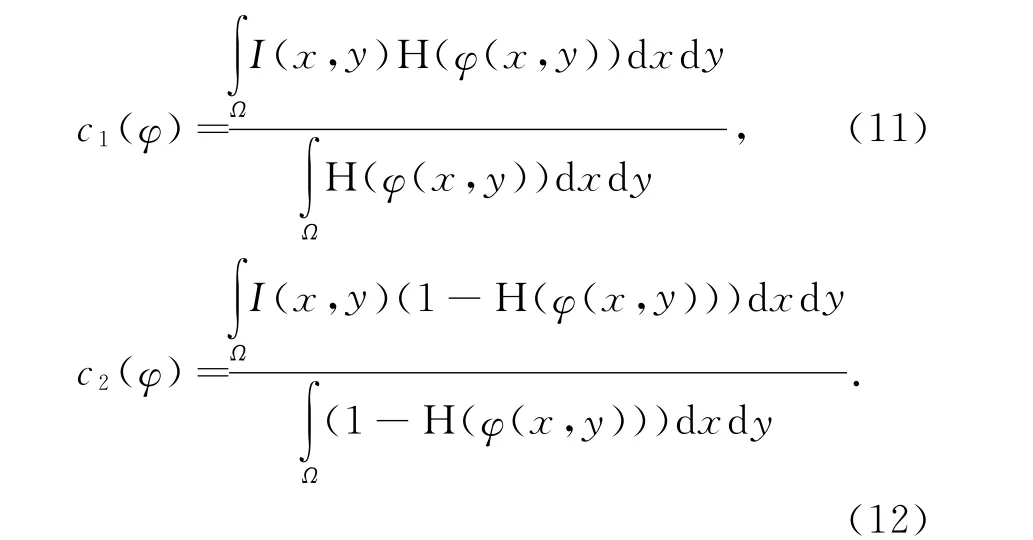
对于固定的c1和c2,采用标准的梯度下降法最小化能量函数.水平集进化的偏微分方程为
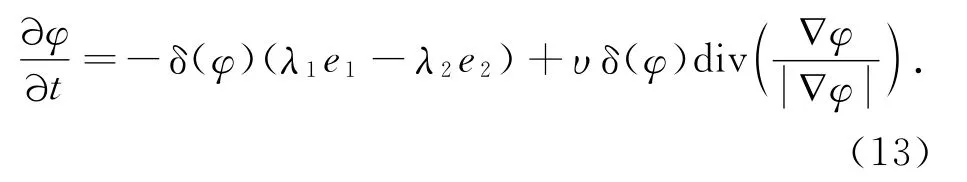
式中,div()表示散度.在进化方程中,第一项负责驱动曲线C逐渐进化到目标边界,第二项负责缩短和光滑进化曲线.为了获取整个目标边界,应该最小化图像区域中所有中心点x的能量函数的积分.
2 数值实现
针对本文提出的局域化水平集模型,需要计算进化曲线上每个点的局域统计量.为了加快水平集的进化速度,仅在由半径r限制的零水平集附近的窄带范围内迭代计算水平集函数.而局域半径r的选取应基于感兴趣目标的尺寸和周围邻近杂斑的情况.例如,当分割具有邻近杂斑的小目标时,应选取较小的局域半径;而当分割具有较少邻近杂斑的大目标时,应选取较大的局域半径.
水平集函数的偏微分项可以由如下有限差分[10]机制作离散化处理:
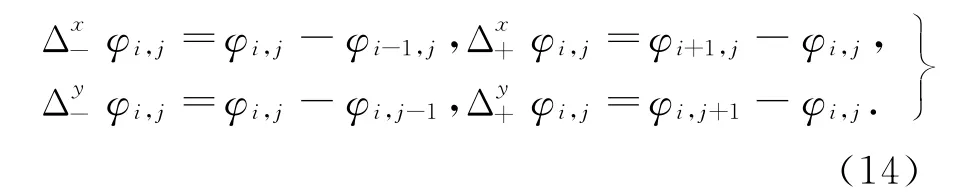
进化方程中的散度项记为L,可作如下离散化处理:
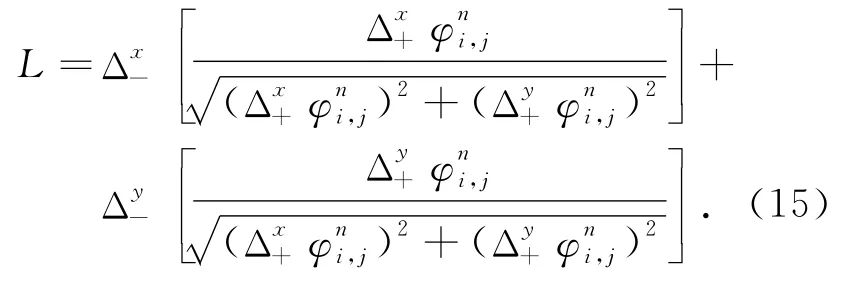
水平集进化过程的计算可分为两步:初始化和迭代更新.而最终的图像分割效果对初始水平集曲线并不敏感,但要求迭代过程中重新初始化水平集,以保证其满足符号距离函数特性.这里如下定义初始水平集函数:
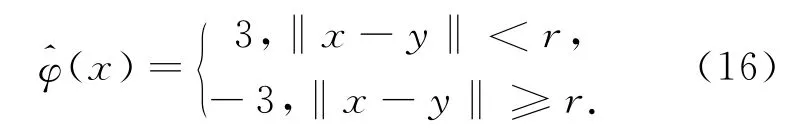
即在局域范围内部将其赋值为正整数3,而在局域范围外部,将其赋值为负整数-3.这里所涉及的整数运算与传统的符号距离初始化函数相比能加快计算速度.而重新初始化水平集的目的是为了重构水平集.因为在进化过程中,水平集函数的梯度方向可能会太陡或者太平,这可能导致数值计算不精确.当初始化像素与进化曲线交叉时,均需重新作初始化处理.本文提出的局域法的缺点是它要处理所有的局部数据统计量,计算量大.
3 实验结果与分析
为了实现鲁棒图像分割,多种方法在模型中引入了形状和灰度分布等先验知识.例如,水平集方法和神经网络方法.其中,水平集方法利用一个闭合曲线的进化实现目标检测,所以能够获得连续的目标边界.下面对这两种方法进行性能比较.
对于具有灰度均匀性的近似分段常值图像,著名的CV模型能得到连续且精确的分割效果.图1中给出了基于CV模型分割一个两目标合成图像的进化过程.图像大小为128×128,水平集参数υ=0.2×255×255.图1中分别用水平集初始轮廓、中间轮廓和最终收敛轮廓描述其进化过程.

图1 两目标合成图像的分割结果Fig.1 Segmentation of a synthetic two-object image
但在实际应用中,特别是对于医学图像,通常存在灰度不均匀性.图2中分别给出了基于CV模型和局域化CV模型分割一人脑MR切片图像的实验结果.图像大小为128×128,水平集参数υ=0.35×255×255.
为了分析和检验当图像存在灰度不均匀性和随机噪声时分割算法的稳定性,从brainweb数据库中选取了多幅仿真脑磁共振图像做仿真实验.这里以其中两幅正常脑解剖T1加权像为例.其噪声分别是0和5%,灰度不均匀性分别为0和20%.图像切片厚度为1.0mm,大小为258×258.
针对神经网络方法,采用自组织映射(SOM)网络模型.为了得到一个满意的映射关系,需要设定好网络的拓扑结构.实验结果表明,六角网格的拓扑结构效果最好.另一个影像分割效果的参数就是网络尺寸.分别采用10×10,11×11,12×12,13×13,14×14,15×15的映射尺寸作测试.随着尺寸的增加,分割效果得到改善.但当网络尺寸大于12×12时,分割效果不再有明显的改善.因此,为了得到更精确的分割结果,同时减少网络运算时间,采用大小为12×12的神经网络[11].
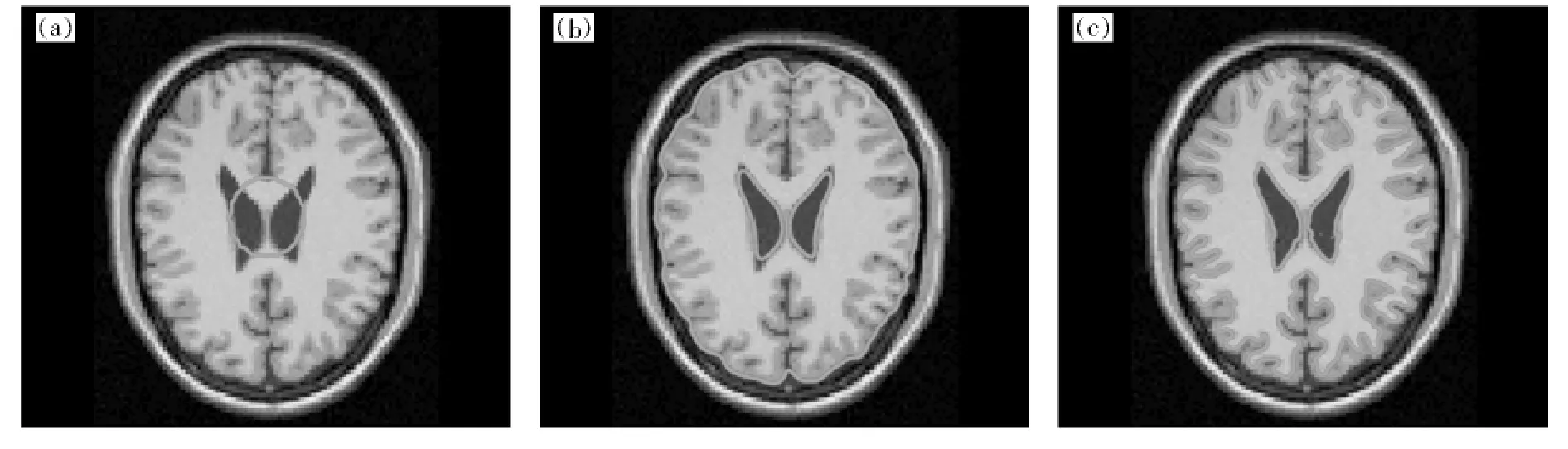
图2 人脑MR切片分割结果Fig.2 Segmentation of a brain MR image
SOM神经网络方法包括两个主要步骤:特征提取和像素分类.在特征提取过程中,提取一个二维归一化的统计向量X=(x1,x2)作为特征向量.该特征向量由像素及其八邻域的归一化均值和方差组成.该向量作为SOM神经网络的输入.对于正常的脑磁共振图像,网络输出节点数为4,分别对应白质、灰质、脑脊液和背景的分类.为了提高网络对噪声的鲁棒性,训练数据由1 000个随机采样的像素点构成.网络迭代数设定为1 000.
针对局域水平集方法,研究了半径参数r对分割结果的影响.实验结果表明,引入局部半径r能增强轮廓内部和外部统计特征的平滑性.半径越大,局部统计特性越平滑.但当提取小目标时,应该选择一个较小的半径.这里令r=7.
水平集模型中的其他参数设置如下:λ1=λ2=1.0,υ=0.001×255×255 ,时间步长 Δt=0.1.图3和图4分别给出了原始脑图像和两种算法的分割结果.
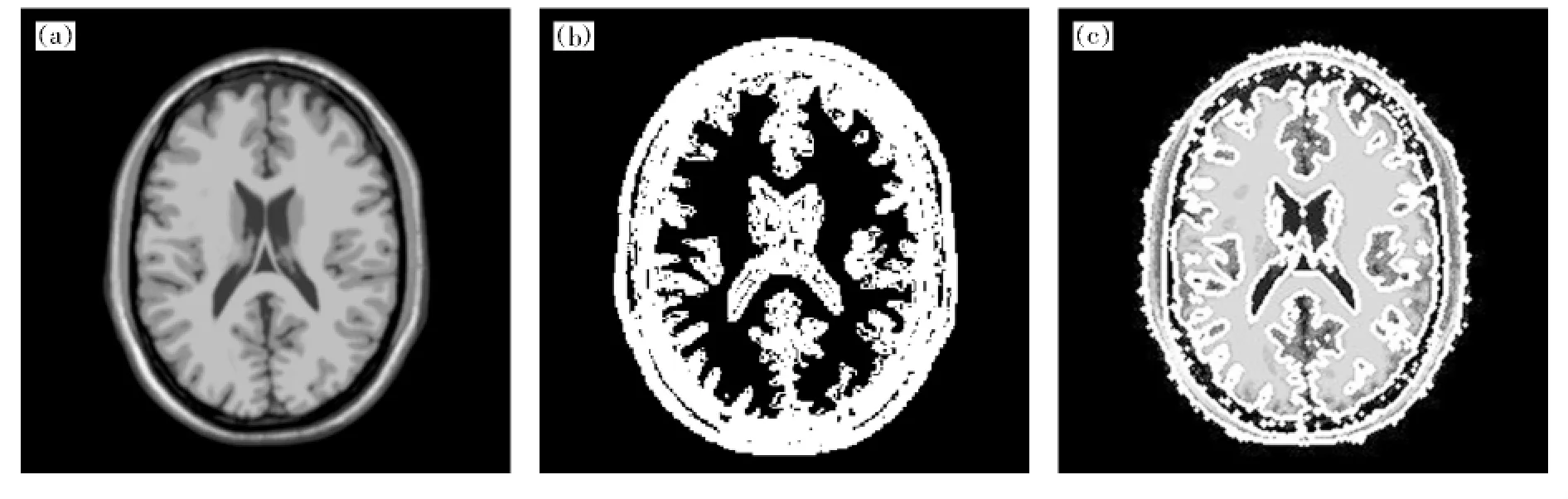
图3 噪声和灰度不均匀性均为0%的仿真MR脑图像的分割结果Fig.3 Segmentation results of a simulated MR image with 0noise level and 0inhomogeneity effect
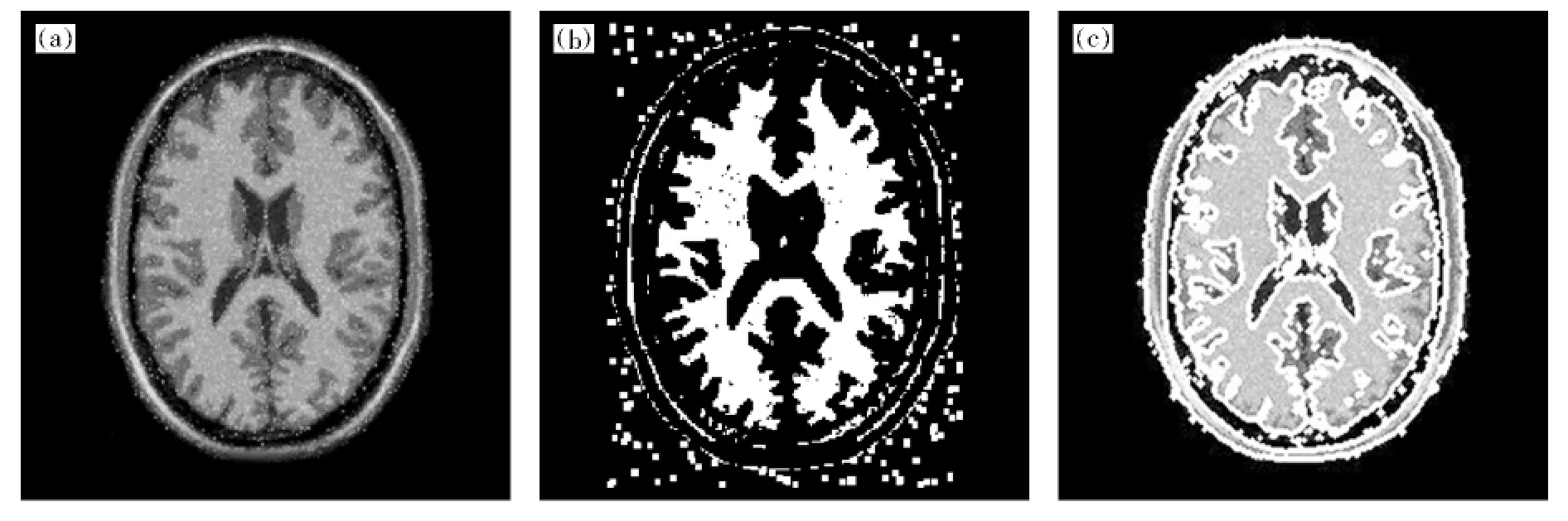
图4 噪声为5%、灰度不均匀性为20%的仿真MR脑图像的分割结果Fig.4 Segmentation results of a simulated MR image with 5%noise level and 20%inhomogeneity effect
仿真结果表明,水平集方法可以提取连续的目标边界,并且在随机噪声和灰度不均匀性存在的情况下鲁棒性更强.
4 结 语
本文提出了一种局域水平集模型用于磁共振脑图像的鲁棒分割.因为水平集方法利用闭合曲线的进化获取目标边界,所以其固有的特性就是能提取连续的目标边界.通过局域化处理,可以提高水平集方法对噪声的鲁棒性,并适用于灰度不均匀性图像的处理.仿真结果表明,与传统的引入先验知识的方法(例如神经网络方法)相比,局域水平集方法在鲁棒去噪和目标边界提取的连续性方面效果更佳.
[1] Li C,Xu C,Gui C,et al.Distance Regularized Level Set Evolution and its Application to Image Segmentation[J].IEEE Trans.Image Processing, 2010,19 (12):3243-3254.
[2] Sanjay Kumar,Santosh Kumar Ray,Peeyush Tewari.A Combined Approach Using Fuzzy Clustering and Local Image Fitting Level Set Method for Global Image Segmentation[J].Canadian Journal on Image Processing and Computer Vision,2012,3(1):1-5.
[3] Antunes S,Silva J,Santos J,et al.Phase Symmetry Approach Applied to Children Heart Chambers Segmentation:A Comparative Study[J].IEEE Trans.Biomedical Engineering,2011,58(8):2264-2271.
[4] Awad M.An Unsupervised Artificial Neural NetworkMethod for Satellite Image Segmentation [J]. The International Arab Journal of Information Technology,2010(7):199-205.
[5] Nadjib Nasri,Karim Mokrani,Abdenour Mekhmoukh.MRI Images Segmentation by FCM and Neighbor’s Statistical Characteristics[J].International Journal of Research and Reviews in Soft and Intelligent Computing,2012,2(1):127-130.
[6] Chan T,Vese L.Active Contours without Edges[J].IEEE Trans.Image Processing,2001(10):266-277.
[7] Li C,Huang R,Ding Z,et al.A Level Set Method for Image Segmentation in the Presence of Intensity Inhomogeneities with Application to MRI[J].IEEE Trans.Image Processing,2011,20(7):2007-2016.
[8] Tsai A,Yezzi A, Willsky A S.Curve Evolution Implementation of the Mumford-Shah Functional for Image Segmentation, Denoising,Interpolation,and Magnification[J].IEEE Trans.Image Processing,2001,10(8):1169-1186.
[9] Bernard O,Friboulet D,Thevenaz P,et al.Variational B-spline Level-set:A Linear Filtering Approach for Fast Deformable Model Evolution[J].IEEE Trans.Image Processing,2009(18):1179-1191.
[10] 郝哲,朱一飞,王铁男.基于差分法的土石坝数值模拟研究[J].沈阳大学学报,2010,22(2):23-27.(Hao Z,Zhu Y F,Wang T N.Numerical Simulation Study on Earth-Rock Dam Based on Calculus of Difference[J].Journal of Shenyang University,2010,22(2):23-27.)
[11] Dan Tian,Linan Fan.MR Brain Image Segmentation Based on Wavelet Transform and SOM Neural Network[C]∥Chinese Control and Decision Conference.Suzhou,2010:4243-4246.

