功能梯度材料板断裂分析

魏 巍，彭 杨，张泽辉，徐启成，张艳艳

（1.沈阳飞机设计研究所，辽宁 沈阳 110035；2.沈阳大学 理学院，辽宁 沈阳 110044；3.辽宁电力勘测设计院，辽宁 沈阳 110179；4.沈阳建筑大学 理学院，辽宁 沈阳 110168）

1984年日本学者［1］率先提出了功能梯度（Functionally Graded Materials，简称FGM）的概念.早期主要应用于航天飞机的防热系统和发动机.与宏观均质复合材料相比，功能梯度材料具有良好的比刚度、比强度及可设计性，其应用领域已从航空航天拓展到核能、生物医学、机械、石油化工、信息、民用及建筑等其他诸多领域.在FGM生产和制备过程中功能梯度材料表面或内部经常出现裂纹或缺陷，在服役过程中，这些裂纹和缺陷会进一步生长，导致FGM在低应力下断裂破坏.因此，研究功能梯度材料的断裂行为很有必要.

FGM的断裂行为研究引起了科研人员的高度重视.Delale和Erdogan［2］采用指数函数形式的物性参数模型和积分变换——奇异积分方程求解技术，对非均匀材料平面裂纹Ⅰ、Ⅱ型问题进行了分析，发现泊松比对裂纹尖端应力强度因子影响非常小.Chen和Erdogan［3］分析了有限厚度功能梯度涂层与均匀半平面基底之间的界面断裂问题.Jin和Noda［4］对比均匀材料和功能梯度材料裂纹前沿位移场并指出：非均匀材料裂纹尖端场的奇异性与均匀材料一致.2001年Chan等人［5］利用位移法分析梯度材料的反平面问题.Erdogan和 Wu［6］针对含有内部和边界裂纹的功能梯度板进行了研究，其中梯度参数为指数形式.Kim等［7］利用有限元法对含有任意方向裂纹的正交各向异性功能梯度材料进行了分析.他们的研究表明对于与材料梯度成任意角度的混合型裂纹问题，裂纹回路积分和位移法可以精确地求解应力强度因子，而且与均匀材料相比，泊松比和边界条件对正交各向异性材料的能量释放率有显著影响.果立成等［8］对含有任意机械属性功能梯度材料进行研究表明：裂纹表面受压时，裂纹尖端以Ⅰ 型开裂为主；裂纹表面受剪力时，裂纹尖端以Ⅱ型开裂为主.果立成和Noda［9］利用奇异积分方程技术将任意机械属性功能梯度材料模型假设分层指数形式，运用这个模型更准确的反映了材料的真实属性.黄干云［10］利用分层模型分析梯度材料在动静态反平面剪切载荷作用下的裂纹问题，计算梯度材料在该模型下的应力强度因子.程站起［11］假设功能梯度材料的剪切模量的倒数为坐标的线性函数，采用积分变换方法，通过求解奇异积分方程获得功能梯度板条Ⅲ型裂纹应力强度因子.李小武［12］等在恒总应变幅控制的条件下研究了含晶界孔洞粗晶工业纯铁的疲劳变形特征，研究结果表明：含晶界孔洞的粗晶工业纯铁随着总应变幅的增加，滑移开裂更趋显著，原来位于晶界上的微观孔洞发生扭曲变形、聚合、长大而产生裂纹，甚至导致沿晶开裂.

本文采用基于非均匀单元的有限元方法对含有中心裂纹功能梯度板平面断裂问题进行研究.在数值计算的过程中引入了非均匀单元，即在积分点处引入材料的真实属性进行计算；采用叠加方法，把应力场转化为裂纹表面载荷.分析了功能梯度材料结构的几何参数及材料属性对裂纹尖端无量纲应力强度因子，并考察了中心裂纹两端应力强度因子的变化规律.

1 建立有限元模型

1.1 利用叠加法简化对称裂纹问题

图1a为无限长功能梯度材料板，其材料属性沿x轴变化，材料沿y轴方向为无限长，裂纹面垂直于y轴，功能梯度板的宽度为h，裂纹的两个端点坐标分别为（a，0）和（b，0）.功能梯度板表面的杨氏模量分别为E1、E2，弹性模量分别取如下两种形式：

式（1）和式（2）分别代表功能梯度板内的几何参数为指数函数和线性函数.

本文利用经典叠加方法，将图1a的模型问题转化为图1b和图1c两个模型问题，由于图1b模型与断裂无关，最终图1a的模型问题可以转化图1c的模型问题，其实质是把应力场转化为裂纹表面载荷.

图1 叠加法简化裂纹问题Fig.1 Superposition method to simplify the crack problem

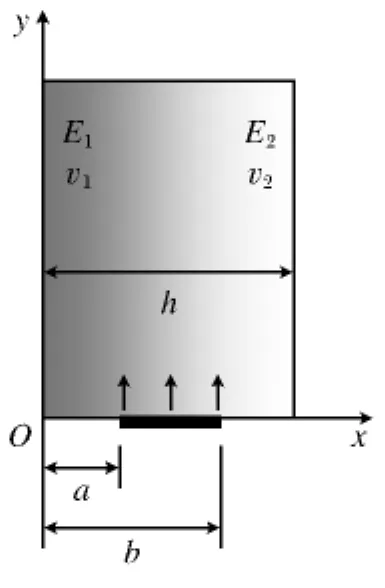
图2 含内部裂纹功能梯度板模型Fig.2 Model of functionally graded material plate with internal crack

有限元建模时充分利用对称性质，将含有裂纹的功能梯度板沿x轴方向在平面内对称剖开，取理论模型的一半为研究对象，利用PATRAN有限元软件建立有限元模型，这样大大减少了建立模型时的工作量.图2和图3分别为实际计算模型图和有限元网格划分图.图3将均布载荷σ0加在了裂纹面上，模型的底端无裂纹位置处加上y方向的约束限制其运动，其中板宽h为200，长L为1 000，L／h＞4，裂纹位于板的中心位置，材料模量比为E2／E1＝0.2，材料采用指数函数形式.计算时两种不同函数形式材料的泊松比取值都为ν＝0.3，即ν1＝ν2.本文问题为二维平面应变问题.

图3 裂纹尖端有限元网格划分图Fig.3 Schematic for crack tip finite element mesh

1.2 基于非均匀单元的有限元方法

本文采用位移法求解裂纹尖端Ⅰ应力强度因子，即

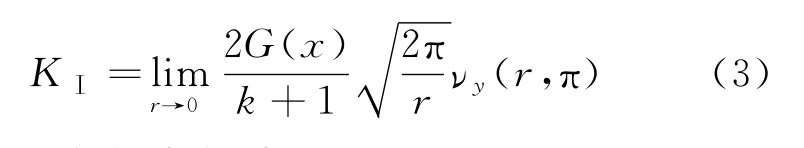
式中，平面应力状态时k＝（3-ν）／（1＋ν）；平面应变状态时k＝3-4ν.G 为剪切模量；νy为裂纹尖端的位移场.

针对功能梯度材料变化的非均匀属性，单元刚度矩阵可以写为

式（4）中D（x，y）为材料属性矩阵，本文采用基于非均匀单元的有限元方法，即在计算单元刚度矩阵时直接取高斯积分点处的实际材料属性进行积分，这样可以使每个单元内部也能够体现材料属性的变化，提高计算精度和效率.同时，为了模拟裂纹尖端的应力奇异性，采用的单元形式如图4所示，将单元前沿线上20节点等参单元的边中间节点移至距裂纹前沿1／4处，这种单元求解应力场在改进的单元边上具有负平方根奇异性.

图4 裂纹尖端单元示意图Fig.4 Schematic for the crack tip element

2 数值结果

2.1 可靠性验证

下面计算裂纹面加载功能梯度板不同裂纹长度的裂纹尖端应力强度因子.本裂纹为张开型Ι型裂纹，内部裂纹的应力强度因子由k0＝σ0进行无量纲化，其中无量纲裂纹中心位置横坐标为（b＋a）／2h＝0.5，无量纲裂纹长度a0为（b-a）／2h，取裂纹无量纲长度分别为 0 .05，0.10，0.15，0.20，0.25，0.30和0.40.表1和表2分别给出了不同无量纲裂纹长度对应的裂纹尖端应力强度因子的数值计算结果，并与理论解析结果比较.从表中可以看到，与Kadioglu［13］和果立成［14］对比裂纹尖端应力强度因子的误差在2%左右，从计算结果可以看出有限元计算方法和理论方法吻合较好，因此本文的数值计算方法是可靠的.

比较表1和表2的计算结果可以看出，①裂纹尖端应力强度因子随着无量纲裂纹长度的增加而增加；②材料的非均匀性导致裂纹两端应力强度因子有显著差别.由于材料模量比为E2／E1＝0.2时，裂纹a端的材料模量高于裂纹b端的材料模量，因此，在裂纹a端的应力强度因子大于裂纹b端的应力强度因子，即在接近刚度大的区域的裂尖无量纲应力强度因子比接近刚度小的区域的裂纹尖端无量纲应力强度因子大.

表1 裂纹a端无量纲应力强度因子与文献的比较Table1 Comparison between reference and stress intensity factor of a-tip for the center crack

表2 裂纹b端无量纲应力强度因子与文献比较Table 2 Comparison between reference and stress intensity factor of b-tip for the center crack

2.2 远场载荷下的中心裂纹问题

无量纲裂纹中心位置横坐标为（b＋a）／2h＝0.5，无量纲裂纹长度为（b-a）／2h＝a0.材料属性分布形式为指数函数形式，材料模量比分别为E2／E1＝0.1和10.内部裂纹的应力强度因子由k0＝进行无量纲化.

图5 中心裂纹a端应力强度因子Fig.5 Stress intensity factor of a-tip for the center crack

图5中，横坐标代表无量纲裂纹长度，纵坐标代表中心裂纹a端的应力强度因子值.图5中给出两条曲线，分别代表不同的模量比对应的应力强度因子.当E2／E1＜1时，功能梯度板x＝h侧的材料模量E2大于x＝0侧的材料模量E1；E2／E1＞1（例如10），功能梯度板x＝h侧的材料模量小于x＝0侧的材料模量.可以看到，当裂纹长度较小时（例如a0＝0.05），随着无量纲裂纹长度的增加，裂纹尖端的无量纲应力强度因子不断增加，当裂纹长度增加到a0＝0.3时，E2／E1＝0.1与E2／E1＝10时的无量纲应力强度因子差别很大，因此，不同的材料的模量比对裂纹尖端的无量纲应力强度因子有一定影响，由计算数据分析可以获知，随着裂纹长度的增加，裂纹尖端靠近模量大的一侧无量纲应力强度因子增加幅度大，这说明材料刚度裂纹尖端的应力强度因子受影响比较大.裂纹尖端无量纲应力强度因子一般随着裂纹尺寸的增大而增大，在模量大的地方裂纹尖端无量纲应力强度因子较大.

3 结 语

功能梯度材料的断裂往往源于材料内部或表面裂纹的扩展，而裂纹的扩展又是从裂纹尖端开始，应力强度因子代表裂纹尖端应力场的强弱.研究结果表明，功能梯度材料结构的几何参数及材料属性对裂纹尖端无量纲应力强度因子的变化规律具有显著影响.

［1］ Koizumi M.FGM Activities in Japan［J］.Composite Part B，1997，28（1／2）：1-4.

［2］ Delale F，Erdogan F.The Crack Problem for a Nonhomogeneous Plane［J］.J.Appl.Mech.，1983，50（3），609-614.

［3］ Chen Y F，Erdogan F.The Interface Problem for a Nonhomogeneous Coating Bonded to a Homogeneous Substrate［J］.J.Mech.Phys.Solid.，1996，44（5）：771-787.

［4］ Jin Z H，Noda N.Crack-Tip Singular Fields in Nonhomogeous Materials ［J］.Journal of Applied Mechanics，1994，61：738-740.

［5］ Chan Y S，Paulino G H，Fannjiang A C.The Crack Problem for Nonhomogeneous Materials under Antiplane Shear Loading-Displacement Based Formulation ［J］.International Journal of Solid and Structures，2001，38（17）：2989-3005.

［6］ Erdogan F，Wu B H.The Surface Crack Problem for a Plate With Functionally Graded Properties［J］.J.Appl.Mech，1997，64（3）：449-456.

［7］ Kim J H，Paulino H G.Mixed-mode Fracture of Orthotropic Functionally Graded Materials Using Finite Elements and the Modified Crack Closure Method［J］.Engineering Fracture Mechanics，2002，69：1557-1586.

［8］ 果立成，吴林志，杜善义.含任意方向裂纹功能梯度材料的应力分析研究［J］.复合材料学报，2004（1）：84-98.（Guo Licheng，Wu Zhilin，Du Shanyi.Stress Analysis of Functionally Graded Materials with an Arbitrarily Oriented Crack［J］.Acta Materiae Compositae Sinica，2004（1）：84-89.

［9］ Guo L C，Noda N.Fracture Mechanics Analysis of Functionally Graded Layered Structures with a Crack Crossing the Interface［J］.Mechanics of Materials，2008，40：81-99.

［10］ 黄干云，汪越胜，佘寿文.功能梯度材料的平面断裂力学分析［J］.力学学报，2005，37（1）：1-8.（Huang Ganyun，Wang Shengyue，She Shouwen.A New Multi-layered Model for In-plane Fracture Analysis of Functionally Graded Materials （FGMS）［J］. Acta Mechanica Sinica，2005.37（1）：1-8.）

［11］ 程站起，卢纪富.功能梯度板条Ⅲ型裂纹问题研究［J］.郑州大学学报，2006.27（4）：89-91.（Cheng Zhanqi，Lu Jifu.A Mode Ⅲ Crack in a Functionally Graded Strip［J］.Journal of Zhengzhou University：Engineering Science，2006.27（4）：89-91.）

［12］ 李小武，曹昕明，允正国.含晶界孔洞粗晶工业纯铁的循环变形及损伤特征［J］.沈阳大学学报：自然科学版，2012（4）：16-22.（Li Xiaowu， Cao Xinming， Yun Zhengguo. Cyclic Deformation and Damage Features of Coarse-Grained Commercially Pure Iron Containing Grain Boundary Voids［J］.Journal of Shenyang University：Natural Science，2012（4）：16-22.）

［13］ Kadioglu S，Dag S，Yahsi S.Crack Problem for a Functionally Graded Layer on an Elastic Foundation［J］.Int.J.Fracture，1998，94：63-77.

［14］ 果立成.功能梯度材料静态与冲击断裂行为的研究［D］.哈尔滨：哈尔滨工业大学，2004.（Guo Licheng.Investigation of the Fracture Behaviors of Functionally Graded Materials under Static and Impact Loads ［D ］. Harbin： Harbin Institute of Technology，2004.）