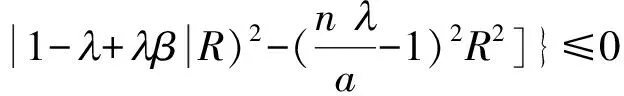推广的非函数的β阶星像性
刘名生
(华南师范大学数学科学学院,广东广州 510631)

刘名生
(华南师范大学数学科学学院,广东广州 510631)


令Hn(p)表示具有如下形式泰勒展开式

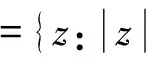





文献[1]和文献[2]分别得到关于M,,α的充分条件,使得由f(z)H1(1)和
(1-)1+Mz


其中0<α<1.SINGH[4]得到如下定理:



OBRADOVIC和OWA[5]得到如下定理:






N(,H1(1):
其中0<α<1,C,-1≤B≤1,A≠B,AR,并且研究了它的从属关系、包含关系、偏差定理和不等式性质.文献[7]研究了某类解析函数子类的性质.一个问题自然提出:是否在适当条件下,这个函数类N(,α,A,B)是星像函数类的子类?
本文的目的是确定关于p,n,,α,β和M的充分条件,使得由
(1-)1+Mz

为了得到本文的主要结果,需要如下引理.
引理1[8]设函数
ω(z)=bnzn+bn+1zn+1+…



引理2 假定0 Q(z) 和 Q(z)pγ(z)1+Mz, Q(z)1+M1z, Q(z)pγ(z)1+M1z, 应用文献[5]中引理2.2的方法,可以证明引理2.引理3是文献[9]中引理2.17的特殊情况. (1) 那么P(z)1+R1z,其中R1=cR/(n-c). 证明令P(z)=1+R1ω(z),R1=cR/(n-c).则ω(z)在U内解析, 且 ω(z)=bnzn+bn+1zn+1+… 我们要证明P(z)1+R1z,只需证明对所有zU,有.用反证法,假定不成立,则存在z0U{0}使得 根据引理1,存在实数k≥n≥1,使得 z0ω′(z0)=kω(z0). 则 这与式(1)相矛盾.因此可得P(z)1+R1z. 注1 在引理4中令n=1,可得文献[3]中相关结果.当n>1时,引理4改进了文献[5]的引理2.1. 引理5 设≠0 是一个实数,[0,1),P(z)H[1,n]和 P(z), (2) 其中 M=Mn(,. (3) P(z)[1-+((1-β)p(z)+β)]1+Mz, (4) (5) 令P=P(z0)=u+iv,则由式(5)可得 2Re{P[1-+(β+(1-β)iρ)]}+1= (u2+v2)2(1-β)2ρ2+2(1-β)vρ+ (u2+v2)2(1-β)2ρ2+2(1-β)vρ+ 定义 G(ρ)=(u2+v2)2(1-β)2ρ2+2(1-β)vρ+ 则W-M2≥G(ρ). 因为(u2+v2)2(1-β)2>0,不等式G(ρ)≥0对所有实数ρ成立,如果判别式 由式(2)可得 (6) 应用式(6)、(2)和(3),经过计算可得 因此Δ≤0,由此可得G(ρ)≥0对所有实数ρ成立,或者W≥M2,因此 这与式(4)矛盾,故引理5得证. 定理1 设>0,0<α (7) 其中幂函数取主值,M=Mn(,pα,β)由式(3)定义,则f). (8) 由式(7)和式(8)可得 (9) P(z). (10) P(z)[1-+((1-β)p(z)+β)]1+Mz. (11) (12) 其中幂函数取主值,且 注2 在推论1和推论2中,令p=n=1,β=0,可得文献[3]中相关结果;在推论1中令β=0,p=1,可得定理B或者文献[5]中定理2.3;在推论1和推论2中,令p=α=1,n=2,β=0,可得定理A或者文献[4]中定理2. 注意到 可得 (13) 其中 M3(). (14) 根据定理1,可得如下定理: 定理2 设>和0 (15) 在推论3中令p=1,可得如下推论: (16) 注3 推论4改进了定理B或者文献[5]的定理2.3;在推论4中令n=2,α=1,可得一个结果,此结果改进了定理A. 定理3 设≥1 和0 (17) 其中幂函数取主值,和 N=Nn(,α,γ)= (18) 证明由0<γ≤1和≥1,有(,pα,0),根据定理1,得fS*(p,0). (19) 由式(17)和式(19),可得 (20) P(z)1+Nz. (21) 因此由式(19)~(21)可得 即 P(z)qγ(z)1+Nz. 因为 根据式(21)和引理2,可得Req(z)>0,U. P(z). (22) 由式(20)和pα/(n-pα)≥1,可得 (23) 所以由式(22)和式(23)可得 即 P(z)qγ(z). 注4 在定理3中令p==1,可得定理C或者文献[5]中的定理2.4. [1] LIU Mingsheng. On certain sufficient condition for starlike functions[J]. Soochow J of Math,2003,29(4):407-412. [2] ZHU Yucan. Some starlikeness criterions for analytic functions[J]. J Math Anal Appl, 2007,335(2):1452-1459. [3] OBRADOVIC M. A class of univalent functions[J].Hokkaido Math J, 1998,27(2):329-335. [4] SINGH V. On a class of univalent functions[J].Internat J Math Math Sci,2000,23(12):855-857. [5] OBRADOVIC M,OWA S. Some sufficient conditions for strongly starlikeness[J].Internat J Math Math Sci,2000,24(9):643-647. [7] 刘志文, 刘名生. 某类解析函数子类的性质与特征[J]. 华南师范大学学报:自然科学版,2010(3):11-14. [8] JACK I S. Functions starlike and convex of orderα[J]. J London Math Soc,1971,3:469-474. [9] PONNUSAMY S,SINGH V. Criteria for strongly starlike functions[J].Complex Variables,1997,34:276-291. LIU Mingsheng (School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China) 2012-01-12 教育部博士点基金项目(20050574002) *通讯作者:刘名生,教授,Email: liumsh@scnu.edu.cn. 1000-5463(2013)01-0014-05 O174.51 A 10.6054/j.jscnun.2012.12.002 【中文责编:庄晓琼 英文责编:肖菁】