基于非线性模型预测的船舶动力定位控制器设计

王元慧，隋玉峰，吴静

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

船舶动力定位(dynamic positioning，DP)是指在有风、浪、流的干扰情况下，不借助锚泊系统，利用本身的推进装置使船舶保持一定的位置和角度或按照预定的运动轨迹运动.动力定位系统主要应用于海上作业船和平台的定点系泊，还可应用于相对潜水器的轨迹控制.其控位精度高、灵活性好，而且成本不会随着水深增加而增加，日益受到重视，得到大力发展.DP系统的控制技术发展到现在可分为3个阶段，第1阶段通常采用常规的PID控制规律，第2阶段以现代控制理论为基础，即最优控制和Kalman滤波理论相结合，第3阶段采用智能控制理论和方法，例如鲁棒控制、模糊控制、神经网络控制、非线性模型预测控制等［1-3］.模型预测控制是20世纪70年代产生，发展至今成为在工业中被广为接受的先进控制技术.它能够显示的处理带有不同类型约束、而控制规律又不能离线计算得到的多变量约束控制问题，而且有提前预测的功能，可以在偏差产生之前就进行校正，对系统参数和环境变化有很好的鲁棒性.国内外对模型预测控制的研究不断深入，取得了很多新的研究成果，例如一些基于非线性模型(Wiener模型、Hammerstein模型、Volterra模型等)的预测控制算法;还有一些与智能控制算法相结合的算法产生，例如模糊预测控制、神经网络预测控制、支持向量机预测控制等［4-6］.Chen在前人的基础上提出了切换解析模型预测控制算法.该算法具有模型预测控制一般特点，并吸取反馈线性化的优点，成为一种重要的算法.张国银等人对Chen提出的切换解析模型预测控制算法进行改进，提出了基于相关度的非切换解析模型预测控制算法，避免了控制器在不同状态间进行切换，有效的避免了系统震荡［7-8］.

本文基于非切换解析模型预测控制理论和方法，设计一种船舶动力定位控制器，使船舶能够快速准确移动到指定位置，并保持位置.

1 船舶仿真系统模型

在风、浪、流共同作用的复杂海况下，船舶在海面上作六自由度的运动.在船舶动力定位中，对于传统水面船，一般只考虑水面3种自由度的运动即可，即:纵荡(surge)、横荡(sway)、艏摇(yaw).在建模中，假设船舶模型的惯性矩阵M以及阻尼矩阵D均为已知，并且均为时不变矩阵，船舶做低速运动，二次项可以忽略不计，最终可以得到三自由度船舶模型如下所示［9-12］:

式中:η=［x y ψ］T为北东坐标系下船舶的北向位置、东向位置和艏向角，v=［u v r］T为船体坐标系下纵向速度、横向速度以及转艏角速度，R(ψ)为北东坐标系与船体坐标系之间的旋转变换矩阵，M为包括刚体质量和附加质量的船舶惯量矩阵，D为阻尼矩阵，τ为控制力和力矩矩阵.它们的结构形式如下:

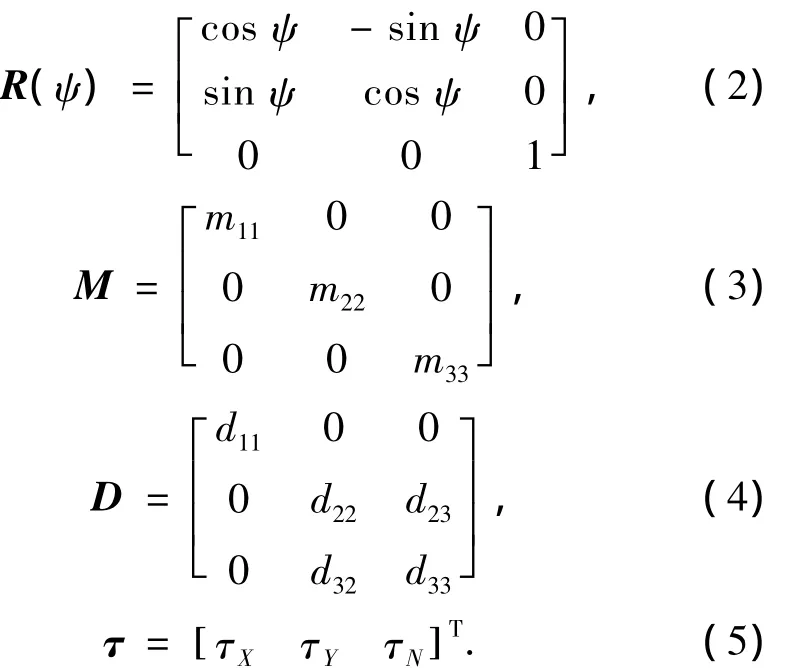
本文控制器的设计理论基于微分方程组形式，因此根据式(2)～(5)，将式(1)展开可以得到船舶方程的微分方程组形式:

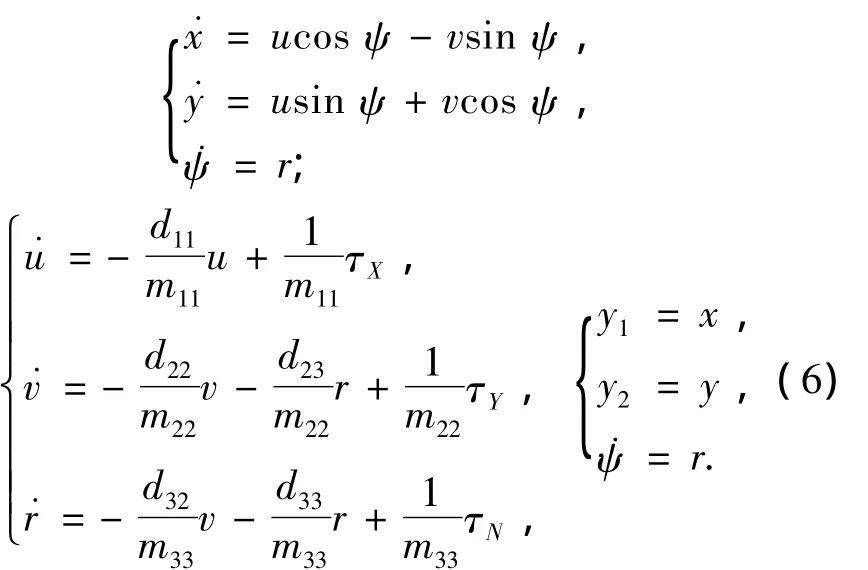
2 动力定位系统控制器设计

2.1 基本概念

定义1 给定一个x= [x1x2… xn]T的标量函数 h(x)与一个向量函数 f(x)=[f1f2…fn]T，则沿着f的李导数定义为

即函数h沿向量场f的李导数就是h在向量场方向的梯度.

高阶李导数定义为

若g是另一个向量场，则

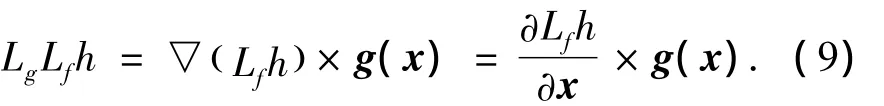
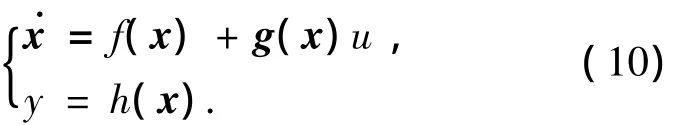
式中:x∈Rn，u∈R，y∈R分别为系统的状态向量、控制输入和系统输出.f(x)、g(x)、h(x)均为光滑的向量函数.假设对上述系统的平衡点 x0有f(x0)=0，h(x0)=0，g(x0)≠0.

定义2 非线性系统称为在x0点处具有确定相关度ρ，如果

考虑单输入单输出的非线性系统:

条件2)说明x0的任意一个邻域内系统都具有相关度ρ.

如果在x0满足=0，而在x0的一个邻域内存在一点满足条件≠0，那么 x0称为奇异点(singular point)，此时称上述非线性系统的相关度不确定(ill-defined).

2.2 控制器设计过程

非线性模型预测控制与传统的线性模型预测控制一样，也是一种基于优化的控制策略，都符合模型预测控制的基本原理:预测模型、滚动优化和反馈校正.由于其本身的非线性特性，最适合用于强非线性、多约束等过程控制系统，因此得到广泛应用.

船舶模型具有非线性、时滞性等特点，考虑其控制的特殊性，本文利用系统相关度概念，根据非线性模型预测控制原理，设计实现控制器.

控制目标是:设计控制器 (τX，τY，τN)使得系统的输出x、y和ψ能够快速准确的移动到设定状态，并且能够保持状态.

假设1 系统输出(x，y，ψ)和期望输出(xd，yd，ψd)连续，可做足够次数的微分运算.

将系统写成如下的规范形式:

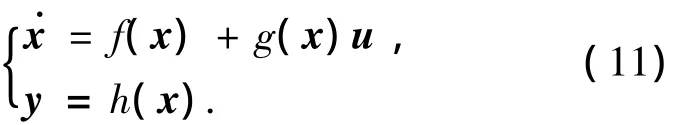
其中，x∈Rn为系统的状态向量，u∈Rl为系统的控制输入，y∈Rm为系统的输出，n=6，l=3，m=3.

其中:

模型预测控制设计需要给出一个具体的性能指标.为了能够综合考虑各个方面的作用，给出一个在滚动时域内的性能指标函数如下所示:

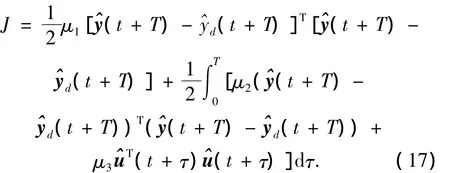
式中:T 是预测周期，μ1、μ2、μ3是非负的(通常情况下，μ2是正数，而 μ1，μ3可以取零)，分别反映了输出终端约束、跟踪误差以及控制量所占的权重;(t+T)和(t+T)分别为系统的输出和期望输出在滚动时域［t，t+T］内的预测值，上标“∧”代表预测值，期望输出的预测值一般是设定值，因此是确定的.

模型预测控制可以表述为在一个滚动时域［t，t+T］内，用 ^x(τ)表示系统状态，用 ^u(τ)表示控制输入，那么系统在滚动时域内的动态方程可表示为

其初始状态即为系统当前状态，即

根据式(18)和(19)的约束下，可以预测［t，t+T］时间段内系统的输出.据此，最小化性能指标J的问题就是寻找［t，t+T］时间段内的最优控制输入^u(t+τ).综上所述，非线性模型预测控制可以描述为:

式(18)和(19)约束.

式(20)与其他的控制思想一样，并不需要计算 τ∈［0，T］内所有的控制输入 ^u(t+ τ)，而只需计算其初始值 ^x(t).实际的控制量u(t)可以采用最优预测控制律 ^u(t+τ)的初始值 ^u(t)，即

综上所述，在非线性预测控制中，系统的控制输入总是取使性能指标J最小的控制输入，并且只关心^u(t+τ)的初始值.当滚动时域时，性能指标J逐渐减小，同时系统输出逐渐接近期望值u(t).在数字控制技术及其工程实践中，通常的控制量是分段函数，因此可以作如下假设:

假设2 控制输入在滚动时域［t，t+T］内假设为常数，即

在这个假设条件下，^u的各阶导数均为零.

为了得到非线性预测控制规律，需要将滚动时域［t，t+T］内系统的输出以及性能指标进行适当阶次的泰勒级数展开.

系统输出^y(t+τ)以及期望输出^yd(t+τ)可以表示为

因此式(17)所示的性能指标J的N阶泰勒级数展开可以近似为

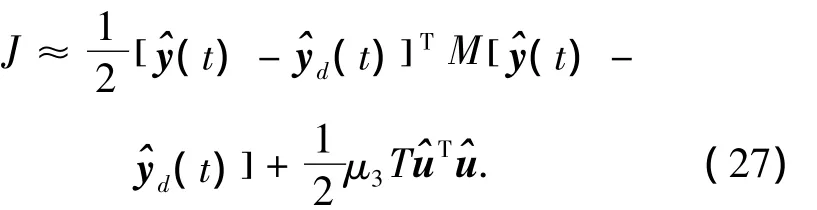
式中

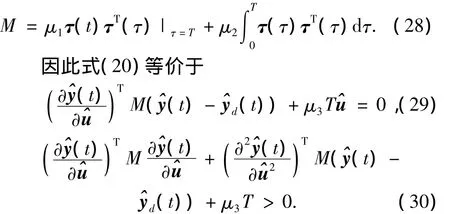
同理，

同理

在这里记

在此讨论一下确定相关度以及不确定关系的问题.从以上的推导公式结合实际得到的值可以看出:对于所有状态x满足Lg3Lfh3=b2≠0，因此从相关度的定义可以看出，ρ3，3是确定相关度，并且 ρ3，3=2，在某些状态 x 为零，这就意味着 ρ11，ρ12，ρ13，ρ21，ρ22，ρ23，ρ31，ρ32是不确定相关度，其中 ρij(1≤i≤l，1≤j≤m)代表控制输出ui到系统输出yi的相关度.

文中选取泰勒级数展开阶次为N=3，选取L=2.记

其中:

且

因此可以将^y(t)重写为

将式(40)、(41)代入到式(29)中，得到方程

式中，

由式(42)，得到非切换解析模型预测控制的解:

取其初值，即为非切换解析模型预测控制的非线性船舶动力定位控制规律:

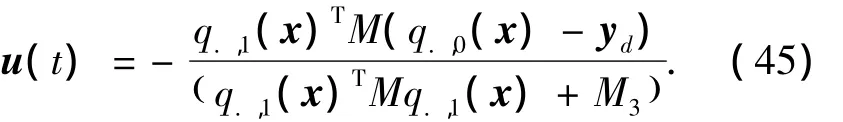
因为 q.，1(x)TMq.，1(x)+M3一定是正定的，具体证明过程在文献［5］中有详细的说明，因此控制规律解决了由奇异点引起的不确定相关度问题;并且该控制规律对所有状态都是连续的，避免了在不同状态之间进行切换引起的震荡，这就是“非切换”控制的由来.

3 仿真验证

为了验证基于非线性模型预测控制规律的有效性，进行如下仿真实验.本文采用某动力定位船作为仿真对象仿真试验，主要参数如表1所示［10-11］.

表1 船舶主要参数Table 1 The parameters of the ship

选取预测周期 T=9.0s，μ1=1.0，μ2=0.000 5，μ3=0.

仿真时间共计500 s，设定仿真时船舶的初始状态和期望状态分别为:

根据上述系统的仿真参数，进行船舶动力定位仿真系统，得到的仿真结果如图1～3.

图1 船舶位置和艏向角Fig.1 The position and heading angle of ship

图2 船舶纵荡、横荡速度和艏摇角速度Fig.2 The Speed and angular velocity of ship

图3 船舶纵向、横向力和艏摇力矩状态Fig.3 The control force and m oment of ship

从以上仿真结果可以看出，将非切换模型预测控制算法应用于DP控制器的设计，船舶动态响应快速，稳定性较好.从仿真曲线也可以看出，北向位置和东向位置有少量超调，但是都收敛较快;艏向角变化范围比较小，但是稳定时间相对较长.

4 结束语

本文利用非线性模型预测控制处理强非线性系统的优势，根据其原理设计了基于非线性模型预测控制算法的船舶动力定位控制器，选择了合理参数，并在无风浪流干扰情况下，验证了非线性模型预测控制器的有效性.仿真结果表明，本文所设计的基于非线性模型预测理论的控制器能够使船舶较快的达到预期状态，证明了非线性模型预测在船舶动力定位上应用的有效性.

［1］韩春生，刘剑，汝福兴，等.基于PID算法的船舶航迹自动控制［J］.自动化技术与应用，2012，31(4):9-12.HAN Chunsheng，LIU Jian，RU Fuxing，et al.Track keeping control for a ship with PID algorithm［J］.Techniques of Automation and Applications，2012，31(4):9-12.

［2］刘胜，杨震.船舶横摇运动实时在线预报方法［J］.电机与控制学报，2011，15(10):82-94.LIU Sheng，YANG Zhen.Real-time online prediction method of ship rolling motion［J］.Electric Machines and Control，2011，15(10):82-94.

［3］严浙平，迟冬南，赵智，等.UUV推进系统模糊自适应融合故障诊断方法［J］.电机与控制学报，2012，16(9):14-19.YAN Zheping，CHIDongnan，ZHAO Zhi，et al.Propeller fault diagnosis for UUV using fuzzy adaptive fusion［J］.E-lectric Machines and Control，2012，16(9):14-19.

［4］赵志高，杨建民，王磊.动力定位系统发展状况及研究方法［J］.海洋工程，2002，20(1):91-97.ZHAO Zhigao，YANG Jianmin，WANG Lei.The development and research method of dynamic positioning system［J］.The Ocean Engineering，2002，20(1):91-97.

［5］夏伟江.动力定位系统(DPS)船舶的产生、发展及在海洋石油勘探、开发、生产等阶段的应用［J］.天津航海，2005(3/4):21.

［6］邹涛，丁宝仓.模型预测控制工程应用导论［M］.北京:化工工业出版社，2010:1-33.

［7］CHEN W H.Analytic predictive controllers for nonlinear systems with ill-defined relative degree［J］.IEEE Proc.-Control Theory Appl，2001，148(1):9-16.

［8］张国银，杨智，谭洪舟.一类非线性系统非切换解析模型预测控制方法研究［J］.自动化学报，2008，34(9):1147-1156.ZHANG Guoyin，YANG Zhi，TAN Hongzhou.Research on non-switch analytic nonlinearmodel predictive controlmethod for a class of nonlinear systems［J］.Acta Automatica Sinica，2008，34(9):1147-1156.

［9］贾欣乐，杨盐生.船舶运动数学建模-机理建模与辨识建模［M］.大连:大连海事大学出版社，1999:7-50.

［10］边信黔，付明玉，王元慧.船舶动力定位［M］.北京:科学出版社，2011:47-49.

［11］王元慧.模型预测控制在动力定位系统中的应用［D］.哈尔滨:哈尔滨工程大学，2006:14-26.WANG Yuanhui.Application ofmodel predictive control to dynamic positioning system［D］.Harbin Engineering University，2006:14-26.

［12］FOSSEN T I.Marine control system:guidance，navigation and control of ships，rigs and underwater vehicles［M］.(s.l.):Marine Cybermetic，2002:104-107.

［13］˚Asmund V˚age Fannemel.Dynamic positioning by nonlinear model predictive control［D］.Norway:Norwegian University of Science and Technology，2008:13-24.

［14］赵大威，边信黔，丁福光.非线性船舶动力定位控制器设计［J］.哈尔滨工程大学学报，2011，32(1):57-61.ZHAO Dawei，BIAN Xinqian，DING Fuguang.Design of a nonlinear controller for dynamic ship positioning［J］.Journal of Harbin Engineering University，2011，32(1):57-61.