非空泡螺旋桨低频线谱噪声时域预报方法

叶金铭，熊鹰，高霄鹏，刘志华

(海军工程大学 船舶与海洋工程系，湖北 武汉 430033)

螺旋桨直接暴露在海水中，由于其旋转引起周围流场变化和压力波动，由此产生的辐射噪声是舰船主要的水下噪声源.在螺旋桨辐射噪声中，低频噪声占据了主要成分，而且低频噪声衰减慢，传播距离远，容易使舰船成为声呐和鱼雷的捕捉目标.为了提高舰船的声隐身性能，迫切需要降低螺旋桨低频噪声的信号特征.1952年，Lighthill从流体基本方程入手，提出了描述声源分布声场的 Lighthill方程[1].1969 年，Ffowcs-Williams等[2]根据 Lighthill方程，应用广义函数法推导出有任意运动固体边界存在时的流体发声的声学公式，即著名的FWH方程，成为螺旋桨噪声理论发展中的一个重要里程碑.用Lighthill方程或广义的Lighthill方程来计算声场辐射的方法，统称为声学类比方法.在20世纪70年代初，大多采用的频域方法预报螺旋桨噪声[3-6]，这主要是因为在当时的条件下时域方法对计算机的配置要求过高，因此在计算过程中一般要作一定的近似处理，比如，噪声源一般是分布在无厚度的拱弧面上，噪声源和观测点的距离也要做一定的近似处理.到了20世纪80年代，Farassa等对FWH进行的巧妙变换[7-9]，得到了适用于亚音速、跨音速情况下的时域内的积分表达式，并给出了相应的求解方法.在此方法中，在固定于叶片的曲线坐标系中严格地规定了各个叶片的几何形状，叶片上的体积脉动噪声源用单极子模拟，压力脉动用偶极子模拟.时域法简单明了，可用同一表达式计算远场和近场，不涉及特殊函数，可对整个叶片表面进行积分计算，不像频域法那样要做薄翼假设.

本文采用基于速度势的面元法预报螺旋桨表面的非定常压力分布，在此基础上，将噪声源直接分布在桨叶表面上进行积分来预报螺旋桨的低频线谱噪声.

1 压力分布及噪声求解方法

1.1 非定常压力求解方法

面元法按照基本控制方程的不同、奇点的不同组合、数值方法的不同以及Kutta条件的不同处理可有多种形式.基于速度势的方法用于非常薄的桨叶切面可以得到更精确的结果;关于单位源和偶的速度势影响系数的奇异性分别比相应的速度影响系数低一阶，因此速度势方法对于非定常面元方法引起的误差的敏感性低一些;另外，关于速度势的影响系数是标量，其所需的计算时间和存储量都小于关于速度的影响系数，而影响系数的计算在整个面元法的计算中占相当大的比例.因此，低阶的基于速度势的面元法，配合非线性的等压 Kutta条件，最适合螺旋桨的计算[10-17].基于速度势面元法的控制方程为

式中:S是螺旋桨表面，SW是尾涡面.

将桨叶上下表面用双曲四边形面元离散，每个面元上布置强度为常值的源汇和偶极子，其值等于面元上控制点(通常取在面元的形心处)处的值，则有

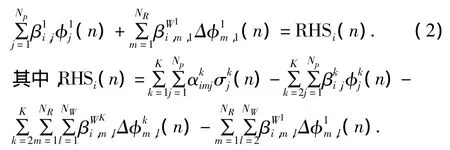
式中:K为桨叶数，上标k表示第k只桨叶;NC和NR分别是弦向和径向面元数;NP=2NCNR是总面元数，NW是尾涡弦向面元数;为影响系数 i=1，2，…，Np.该式表示在每一时间步 n只需对主叶(k=1)求解.出现在等式右端的其他叶片(k＞1)上的φ及尾涡面上的Δφ均取主叶在此前某一时间步处于该位置时的相应值，这种方法是求解式(2)的基本迭代方法，在多数情况下计算7～10周即可收敛.

为了验证本文面元法的计算精度，本文对22届ITTC面元法研讨会提供的一只大侧斜五叶桨(编号为HSP)的非定常性能进行了计算.将非定常压力分布的计算结果同试验测试结果以及Hoshino的计算结果进行了比较，比较结果见图1、2，由图可见，本文的计算结果和Hoshino的计算结果吻合得很好，叶切面的压力分布形式以及随时间变化的规律与试验测量也有较好的一致性.说明本文的关于螺旋桨非定常性能的计算方法和编制的程序是稳定可靠的.

图1 HSP r/R=0.7处剖面在0°角位置的压力分布比较Fig.1 The pressure distribution comparison of the HSP propeller at r/R=0.7

图2 HSP桨0.7叶切面25%弦向位置旋转一周过程中的压力脉动Fig.2 The unsteady pressure comparison of the HSP propeller at r/R=0.7，25%chord location

1.2 噪声求解方法

1969年Ffowcs Williams根据Lighthill的声学类比方法，推导出有任意运动固体边界存在的流体发声的声学公式[6]，即著名的 FWH方程，FWH方程如下:

式中:PT＇表示由厚度导致的声压，对应于单极子表示负载引起的声压，对应于偶极子，Farassat给出了这2种噪声声压的积分公式:

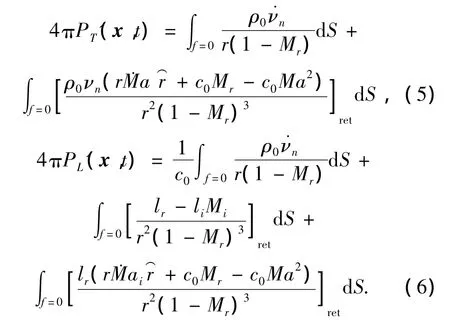
式中:Ma为马赫数，Mr径向马赫数，li是i方向单位面积的局部作用力.

2 计算结果及分析

对DTRC4118桨的在非均匀来流中的水动力性能进行计算，进速系数 J=0.833，螺旋桨转速为960 r/s，来流速度为 6.4 m/s，螺旋桨直径 D=0.480 2 m，伴流分布采用Boswell在试验中形成的三峰值伴流，各半径处的轴向伴流如图3所示，其中0°位置为螺旋桨的正上方，从船尾向船首看，定义角度顺时针为正.

对螺旋桨用双曲四边形面元离散，弦向面元数NC=20，径向面元数NR=20，尾涡弦向面元数NW=80，分别为每一周的时间步数为120，用时域迭代方法在主叶上进行求解.计算得到的0.71R叶剖面在不同角度的压力分布曲线如图4所示，螺旋桨推力系数三阶轴频谐调幅值计算结果为0.066 4，实验测量值为0.065 6，螺旋桨扭矩系数三阶轴频幅值计算结果为0.009 99，实验测量值为 0.01，可以看出本文的计算结果与试验结果很接近.

图3 三峰值伴流分布Fig.3 Wake distribution

图4 0.71R叶剖面在不同角度的压力分布曲线Fig.4 The pressure distribution of 0.71R section at different angles

通过面元法计算得到螺旋桨上的非定常压力分布后，通过式(5)、(6)可以分别计算得到螺旋桨的厚度噪声和负荷噪声.计算时，水的密度取1 026 kg/m2，声速为1 500 m/s，计算噪声级时的参考声压为1.0 MPa.设观测点距离螺旋桨中心的距离为d，方位角为θ，如图5所示.

图5 观测点位置示意Fig.5 Observer position

对观测点 d=20R，θ=0°和 θ°=90°处噪声声压进行了计算，总声压随时间的变化如图6所示，各阶叶频噪声声压级如图7所示.从图可以看出，d=20R，θ=90°处的声压变化幅值和声压级明显要比d=20R，θ°=90°处高，这说明非空泡螺旋桨的噪声有明显的方向性.从图7还可以看出，高阶声压级比一阶声压级明显要低，说明非空泡条件下，一阶叶频声压占据了声压的主要成分.

图6 总声压随时间的变化曲线Fig.6 Overall acoustic pressure time histories

为了分析不同噪声源对噪声声压的贡献，分别计算了桨叶负荷、桨叶厚度、桨毂负荷、桨毂厚度引起的噪声声压，如图8所示.可以看出，桨叶厚度、桨毂负荷引起的噪声声压非常小，虽然桨毂厚度引起的噪声声压比较明显，但随着时间的变化非常小，因此对声压级的贡献也是可以忽略不计的.

图7 总声压级Fig.7 Overall sound pressure level

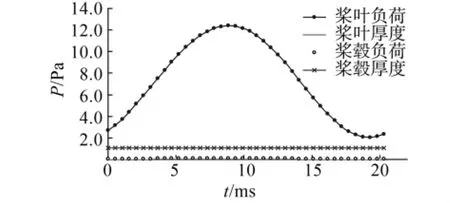
图8 d=20R，θ=0°处不同声源引起的噪声声压随时间的变化曲线Fig.8 Acoustic pressure time histories of various sources at d=20R，θ=0°

为了研究网格疏密对计算结果的影响，采用另一种网格划分形式(NC=30，NR=30)对水动力和噪声进行了计算，噪声声压和声级的计算结果与原来网格划分的计算结果进行了比较，如图9所示，可以看出两种网格化划分形式下得到的计算结果差别很小，因此可以认为原来的网格划分方法对计算非空泡螺旋桨的低频线谱噪声已经足够.

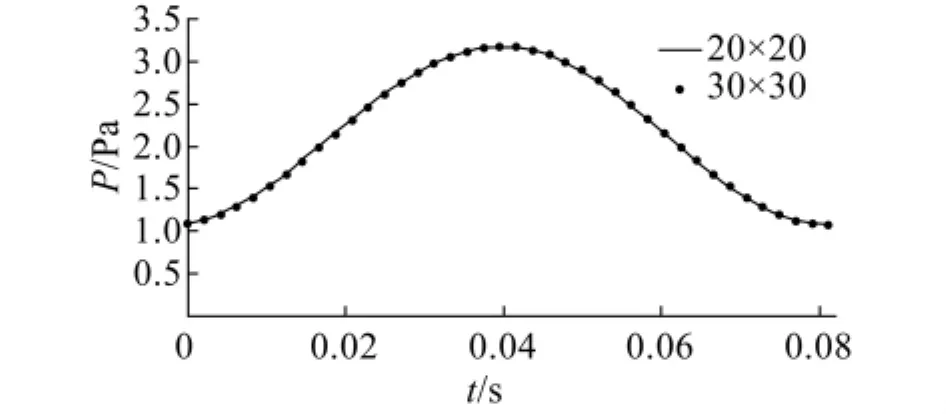
图9 d=20R，θ=0°处不同网格划分条件下的声压计算结果比较Fig.9 Acoustic pressure time histories and SPL with different mesh dicretizations at d=20R，θ=0°

本文还考虑了时间步对噪声计算的影响，图10是时间步数为240时的计算结果与原时间步计算结果的比较情况，可以看出两者的差别也很小，说明原来的设定的每周120步的时间步数已经足够.

从图6可以看出，在相同观测距离的条件下，θ=90°的噪声声压比θ=0°的声压小许多，为了进一步探讨螺旋桨辐射噪声的方向性，本文计算了360°范围内各点的声压级，其中不同方向上1阶声压级分布如图11所示，可以看出，不同方向上的声压级呈“8”字形，在桨轴方向上，声压级是最大，在桨盘面方向声压级最小.

图10 d=20R，θ=0°处不同时间步条件下声压计算结果比较Fig.10 Acoustic pressure time histories and SPL with different time steps at d=20R，θ=0°

图11 d=20R处不同θ角处的一阶叶频噪声总声级Fig.11 The first blade frequency SPL at different angles θ at distance 10R

3 结束语

用时域方法计算了螺旋桨非空泡状态的低频线谱噪声.通过基于速度势的面元法计算得到螺旋桨的非定常压力分布，将压力分布代入Farrasat的噪声积分方程中，得到观测点的声压.通过对DTRC4118桨的计算结果显示，桨叶厚度、桨毂负荷引起的噪声声压非常小，虽然桨毂厚度引起的噪声声压比较明显，但随着时间的变化非常小，因此对声压级的贡献也是可以忽略不计的.同时还分析了非空泡螺旋桨噪声的方向特性和频率特性，高阶叶频声压级比一阶声压级明显要低，说明非空泡条件下，一阶叶频声压占据了声压的主要成分;不同方向上的声压级呈“8”字形，在桨轴方向上，声压级是最大，在桨盘面方向声压级最小.本文的计算方法有较好的稳定性和计算精度，可以较好地考虑桨毂对辐射噪声的影响，本文的方法可用于预报螺旋桨的低频线谱噪声预报.

[1]LIGHTHILL M J.On sound generated aerodynamically，I:general theory[J].Proceedings of the Royal Society，1952，211(1107):564-587.

[2]WILLIAMS J E，HAWKING D L.Sound generated by turbulence and surfaces in arbitrary motion[J].Philosophical Transactions of the Royal Society，1969，A264(1151):321-342.

[3]HANSON D B，FINK M R.The importance of quadrupole sources in prediction of high speed propeller noise[J].Journal of Sound and Vibration，1979，62(1):19-38.

[4]HANSON D B.Helicoidal surface theory for harmonic noise of propellers in the far field[J].AIAA，1980，18(10):1213-1220.

[5]HANSON D B.Influence of propeller design parameters on far-field harmonic noise in forward flight[J].AIAA，1980，18(11):1313-1319.

[6]ZHU Xiqing，TANG Denghai，SUN Hongxing，et al.Study of low-frequency noise induced by marine propeller[J].Journal of Hydrodynamics，Ser.B，2000，15(1):74-81.

[7]FARASSAT F，BROWN T J.A new capability for predicting helicopter rotor and propeller noise including the effect of forward motion[R].New York:NASA，1977.

[8]FARASSAT F，SUCCI G P.The prediction of helicopter discrete frequency noise[J].Vertica，1983，7(4):309-320.

[9]FARASSAT F，BRENTNER K S.The uses and abuses of the acoustic analogy in helicopter rotor noise prediction[J].Journal of the American Helicopter Society，1988，33(1):29-36.

[10]KERWIN J E，KINNAS S A，LEE J T，et al.A surface panel method for the hydrodynamic analysis of ducted propellers[J].Transactions of SNAME，1987，95(1):93-122.

[11]HSIN C Y.Development and analysis of panel methods for propellers in unsteady flow[D].[s.l.]:MIT，Department of Ocean Engineering，1990:70-108.

[12]KINNAS S，FINE N.A nonlinear boundary element method for the analysis of unsteady propeller sheet cavitation[C]//19th Symposium on Naval Hydrodynamics.Seoul，Korea，1992:102-112.

[13]XIONG Ying，YE Jinming，WANG Dexun.Prediction of unsteady cavitation of propeller using surface panel method[J].Journal of Hydrodynamics，Ser.B，2005，17(1):43-49.

[14]YE Jinming，XIONG Ying.Prediction of podded propeller cavitation using unsteady surface-panel method based on velocity potential[J].Journal of Hydrodynamics，Ser.B，2008，20(6):790-796.

[15]YE Jinming，XIONG Ying.Prediction of 3-D hydrofoil and propeller cavitation using BEM method by pressure Kutta condition[J].Journal of Ship Mechanics，2008，12(3):335-343.

[16]叶金铭，熊鹰.螺旋桨空泡数值分析[J].哈尔滨工程大学学报，2006，27(2):172-175.YE Jinming，XIONG Ying.Numerical analysis of propeller cavitation[J].Journal of Harbin Engineering University，2006，27(2):172-175.

[17]叶金铭，熊鹰.预报脉动压力的几种方法[J].哈尔滨工程大学学报，2008，29(12):1266-1271.YE Jinming，XIONG Ying.Several methods for predicting pressure fluctuations[J].Journal of Harbin Engineering University，2008，29(12):1266-1271.