噪声环境下单矢量水听器高分辨定向技术研究

陈羽，王伟，王建飞，马树青，孟洲

(国防科技大学 光电科学与工程学院，湖南 长沙 410073)

在水声探测中，单个标量水听器无法实现对目标的定向，因此常采用声压水听器阵列接收目标辐射的声信号，通过阵列信号处理［1-2］对目标方位(direction of arrival，DOA)进行估计.矢量水听器由于自身具有自然指向性，单个传感器就可以实现对目标的定向.近年来，水声探测载体对水听器系统小型化要求越来越高，单矢量水听器无疑最大限度地节省了系统占用的空间，因此研究单矢量水听器高分辨定向方法就显得尤为重要了.

近年来，国内外关于单矢量水听器方位估计技术研究发表了很多文章［3-6］:平均声强器对于多目标的分辨无能为力，复声强器较多用于辐射线谱目标的测量.常规波束形成器受到“瑞利准则”的限制，无法分辨2个在方位上靠得很近的信号源.MU-SIC算法［7］是较为经典的高分辨DOA估计方法之一，从理论上克服了“瑞利准则”，但该算法一般具有稳健性差、方位分辨信噪比门限较高等缺点.当阵列流型失配或接收信号信噪比较低时方位估计性能会急剧下降，出现大的偏差甚至产生错误的估计.对传统阵列而言，阵列流型随着阵列水下形状的变化而变化，而单矢量水听器本身具有偶极子指向性，具有固定的阵列流型.考虑到空域矩阵滤波［8］预处理可以净化数据，提高信噪比，提出了基于单矢量阵列流型的空域滤波预处理方法.

1 算法理论及仿真计算分析

1.1 常规MUSIC算法

1.1.1 单矢量水听器的常规MUSIC算法

单矢量水听器本身具有阵列流型特性，可以看作一个小型的三基元阵列.为叙述简明，不失一般性，忽略声阻抗ρc，声压信号P以及水平振速的2个正交分量Vx与Vy可以表示为

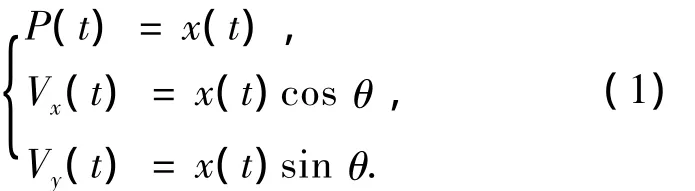
式中:x(t)是声压信号，它是无指向性的，是标量.振速信号是矢量;本身具有偶极子指向性;θ是入射声波的水平方位角，θ的取值范围为［0，2π］.

根据单矢量水听器数学模型，假定有K个远场窄带平面波信号从 K 个方向 θk= ［θi…θd…θK］入射到单矢量水听器的流型固定阵列处，则第d个窄带信号在单矢量水听器上的阵列流型为

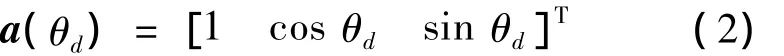
式中:第1项到第3项分别对应声压信号、X通道的振速信号、Y通道的振速信号.式(2)所描述的阵列流型实际相当于一个3×1维的阵列流型，它本身不包含时延信息，但包含了目标的方位信息.

模仿阵列数据模型，这3个阵元接收到的快拍数据写成矩阵形式为

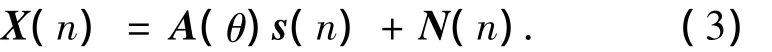
式中:A(θ)=［a(θ1)…a(θd)…a(θK)］是3 ×K维阵列流型矩阵;s(n)=［s1(n)…sK(n)］是K×1维信号源向量;N(n)是3×1维噪声向量.

假定噪声与信号不相关，数据协方差矩阵可以表示为

式中:Rs与Rn分别为K×K维信号协方差矩阵以及3×3维噪声协方差矩阵.根据子空间分解理论，如果信号源的个数少于阵列阵元个数，那么阵列数据的信号分量位于数据协方差矩阵R的一个低秩空间.对矩阵R进行特征值分解得到

式中:Λ是按从大到小顺序排列的特征值构成的对角阵，E=［EsEn］是对应的特征向量，Es与En分别是由较大的K个特征值与较小的3－K个特征值对应的特征向量组成的信号子空间与噪声子空间.假定信源数K已知且K＜3.

此时信号子空间与入射信号的导向矢量a(θ)张成的空间是同一个空间，在理想条件下，数据的信号子空间与噪声子空间正交，即入射信号的导向矢量与噪声子空间正交.利用这一特性可以构造单矢量水听器MUSIC空间谱:

一般情况下，由于噪声的存在，入射信号的导向矢量与噪声子空间无法做到完全正交，因此实际方位估计是以角度θ搜索使得MUSIC空间谱PMUSIC(θ)最大实现的.

1.1.2 噪声环境下常规MUSIC算法性能仿真研究

首先分析单矢量水听器MUSIC算法对单个目标的定向性能.仿真中采用窄带信号源从水平方位角70°的方向入射至水听器，信号叠加了零均值的高斯噪声，噪声各向同性.样本采样率为10kHz，采样点数为1 024，角度扫描范围为0～180°，扫描间隔为0.5°.分别讨论不同信噪比情况下常规MUSIC

算法方位估计性能如图1所示.

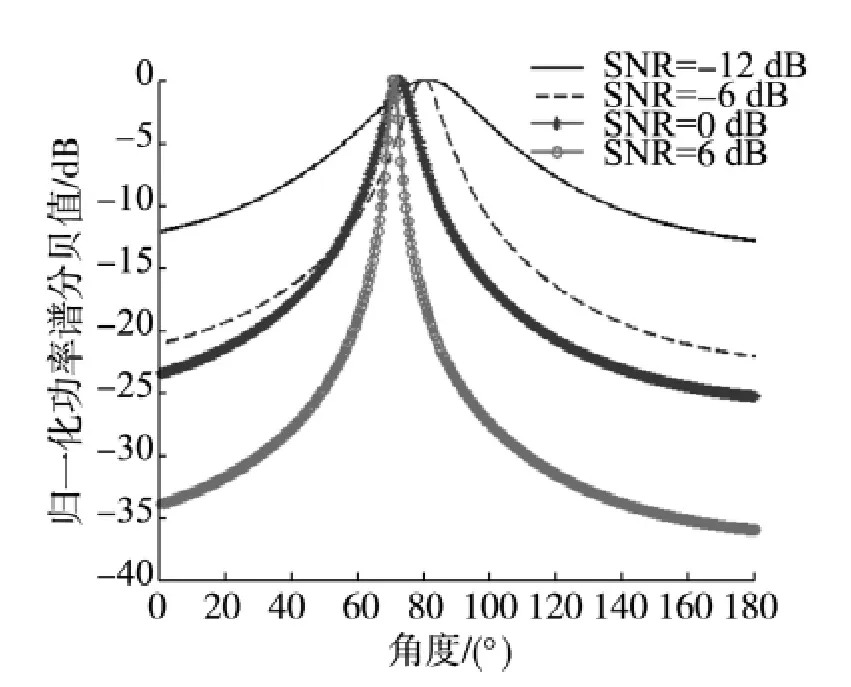
图1 常规MUSIC算法单目标定向性能Fig.1 The DOA performance for single target of routine MUSIC algorithm

观察图1可知，接收信号SNR＞0 dB时，单矢量水听器可对窄带信号实现准确定向，且随着信噪比的增大，主瓣宽度减小，定向性能得以改善.当SNR＜0 dB时，波束峰值偏离了目标的准确方位，且信噪比越低，主瓣越宽，定向准确性越差.当SNR=-6 dB时方位估计值约为80°，主瓣宽度接近20°，已无法实现对目标的准确定向.

MUSIC算法也能对多目标进行分辨，下面分析单矢量水听器对双目标的定向性能.假定2等强度非相关窄带噪声源分别从40°和50°的方向入射到矢量水听器处，背景噪声为与信号不相关的高斯白噪声，噪声各向同性，2信号源的信噪比相同.改变信噪比大小，定向结果如图2所示.

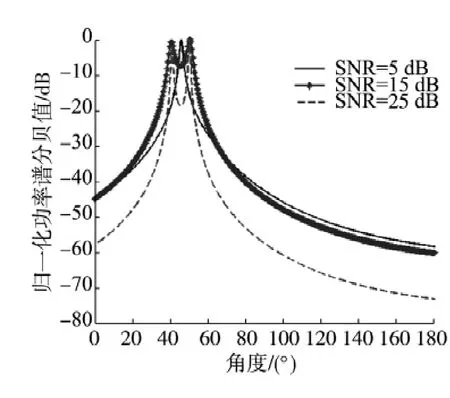
图2 常规MUSIC算法双目标定向性能Fig.2 The DOA performance for double targets of routine MUSIC algorithm

由图2可知，接收信号信噪比越高，定向结果图中2个目标峰值越明显，即越容易区分2个目标的方位.当SNR=5 dB时，单矢量水听器已经无法区分水平方位相差10°的2个目标.

上述仿真结果说明了常规MUSIC算法方位分辨信噪比门限较高，信噪比较低时定向性能急剧下降.

1.2 改进MUSIC算法

1.2.1 基于矩阵空域预滤波的改进MUSIC算法

矩阵空域滤波是一种阵列波束优化技术中采用的方法，可以使阵列接收信号得到净化，信噪比提高.由于单个矢量水体器也有自身固定的阵列流型，可视为一个三基元的阵列，因此可以尝试将矩阵空域滤波方法应用于单矢量水听器.

对于式(3)所示的单矢量水听器阵列数据模型，空域滤波器可表示成一个3×3维矩阵H，由矩阵相关知识可知对阵列数据进行滤波实际是将滤波器矩阵与阵列数据矩阵相乘，因而经空域滤波预处理后输出为

矩阵H实际构造了一个空域带通滤波器，将整个空域(0，-2π)分为通带 θp与阻带 θs两部分，通带应当包含目标所在的真实方位角，在通带内信号可以无失真地通过，而阻带内信号通过后输出为0.也就是说，空域滤波器抑制了不感兴趣方位的噪声信号，使得通过通带的信号信噪比较之滤波前有明显的提高.则该空域滤波器应当满足:

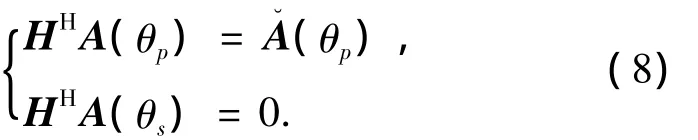
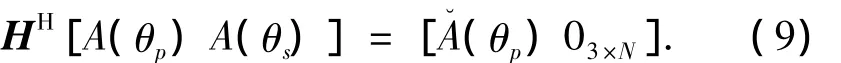
令 A= ［A(θp)A(θs)］= ［(θp)03×Ns］，则式(9)可以化为:

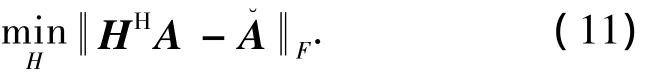
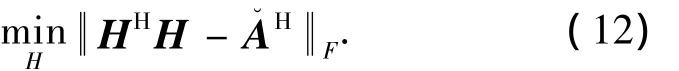
最终解得［9］

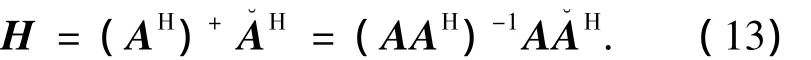
(·)+表示伪逆.

将式(13)解得的结果代入式(7)，得到经过空域滤波预处理后的输出信号，只要通带及阻带选择恰当，理论上可以显著提高输出信号的信噪比.将滤波后的信号求解数据协方差矩阵，对其进行特征值分解构造与常规MUSIC算法类似的方位谱，由于设计出的矩阵滤波器通带响应HHA(θp)与期望响应(θp)之间存在一定的误差，因此需要对MUSIC方位谱表达式做适当改进，以消除通带响应向量畸变的影响，改进后的方位谱表达式为c(θ)=HHa(θ)表示空域滤波后的阵列流型向量，Ecn是滤波后的信号数据协方差特征值分解后的噪声子空间.

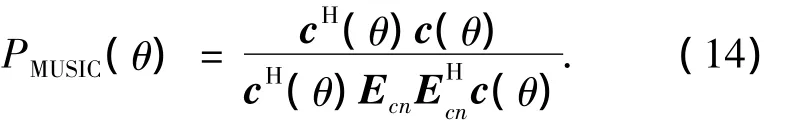
1.2.2 噪声环境下改进算法性能仿真分析

通过1.1.2节分析可知:常规MUSIC算法在低信噪比环境下对目标的定向性能显著下降.矩阵空域滤波器可以净化数据，提高信噪比.因此改进的MUSIC算法能提高噪声环境下的定向性能.

首先讨论不同信噪比条件下改进MUSIC算法对单个目标的定向性能.采用窄带信号源从水平方位角70°的方向入射至水听器，信号叠加了零均值的高斯噪声，噪声各向同性.设定矩阵空域滤波器通带范围［60°:1°:80°］，阻带范围［1°:1°:59°］∪［81°:1°:360°］.对200 次独立观察的数据进行方位估计，定向结果误差在［-1°，1°］范围内认为定向正确，定义分辨概率为正确定向的次数与观察次数的比值.各信噪比条件下分辨概率统计结果如图3所示.

图3 分辨概率随信噪比变化Fig.3 The resolving probability with different SNRs

图4 主瓣宽度随信噪比变化Fig.4 The beam width with different SNRs

由图3、4可知，当SNR＜5 dB时，改进MUSIC算法方位分辨概率明显高于常规算法.SNR=-15 dB时，常规算法方位分辨概率几乎为零，已完全无法对目标方位进行准确估计，而采用改进算法其分辨概率接近0.6，其定向结果有一定的可信度.随着信噪比的提高，2种算法对应的分辨概率变大，且越来越接近，当SNR＞5 dB时2种算法都能准确对目标方位进行估计.同时，当SNR＜0 dB时，改进后的MUSIC算法对应的主瓣宽度明显较常规算法小，这也证明了在低信噪比条件下，改进后的MUSIC算法能提高方位分辨率，可应用于单矢量水听器高分辨方位估计.

改进MUSIC算法同样能提高对噪声环境下多目标的分辨能力.假定多目标信号源与1.1.2节叙述相同，设定矩阵空域滤波器通带范围［35°:1°:55°］，阻带范围［1°:1°:34°］∪［59°:1°:360°］.规定对多目标的判定准则为:

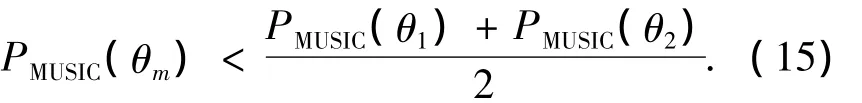
θ1和 θ2表示目标的真实方位PMUSIC(·)表示空间谱.

对200次独立观察的数据进行方位估计，满足式(15)，认为可以正确分辨2个目标，定义分辨概率为正确分辨2个目标的次数与观察次数的比值.各信噪比条件下分辨概率统计结果如图5所示.

图5中SNR＜-5 dB时两种算法对双目标的分辨概率都为0.当SNR＞-5 dB时改进的MUSIC算法分辨率显著提高，且都高于常规算法.当SNR=5 dB时改进MUSIC算法分辨率达到了0.9，常规MUSIC算法分辨率仅为0.2.当SNR＞15 dB时改进算法分辨率已经接近1，此时常规算法分辨率仍只有0.5.相比常规算法，改进后的MUSIC算法对多目标的分辨能力显著提高.

图5 改进MUSIC算法双目标定向性能Fig.5 The DOA performance for double targets of improved MUSIC algorithm

2 试验数据处理

为了验证算法的有效性，处理了东江湖上试验数据.整个试验采用双船作业方式，如图6所示.发射船载有声源，声源发射扫频信号，整个试验设定有若干站点，发射船行驶至站位点停船发射信号，信号频带范围为630～1 000 Hz，采样率为16 kHz.探测船上有沉底矢量水听器一套，用于接收发射船信号.水听器系统装有电磁罗盘，沉底姿态由电磁罗盘监控，整个试验过程中水听器俯仰角及横滚角均小于3°.

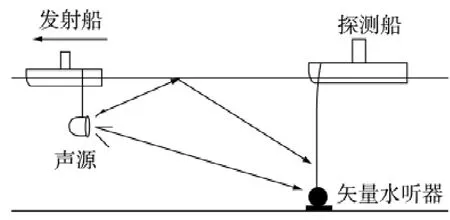
图6 试验示意图Fig.6 Schematic diagram of the experiment

选取距离探测船3.5 km处站位点采集的信号，总共持续时间约为24 s，分别采用常规以及改进2种算法对声源目标方位进行估计，选择其中一组数据方位估计结果如图7所示.

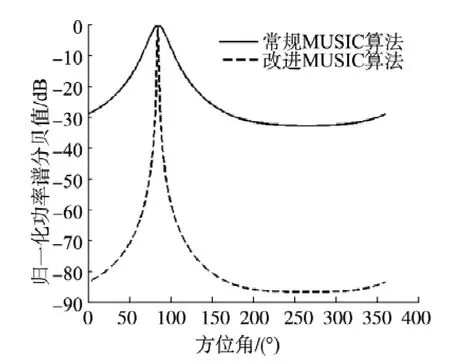
图7 定向结果Fig.7 The DOA estimation

常规MUSIC算法定向结果为85°，改进算法的定向结果也为85°，即估计目标相对矢量水听器+X轴夹角为85°.整个试验过程中电磁罗盘水平方位角示数为122°，经姿态校正后目标在地理坐标系中的航向角(与正北方向夹角)为37°.由发射船与探测船GPS坐标计算得出目标航向角为34.82°，考虑到GPS误差及电磁罗盘安装精度，可以认为2种算法都准确实现了对目标的方位估计.

相比常规MUSIC算法，改进后的算法定向波束更尖锐，方位分辨率得以显著提高，能更准确地对目标运动实施跟踪.

最后处理了一段发射船围绕探测船做近似圆周运动时采集的数据.以探测船的辐射噪声作为信号源，选择频段为300～600 Hz的信号进行处理，得到目标时间方位历程图如图8、9所示.

图8 常规MUSIC算法航迹Fig.8 M ap of the traditional MUSIC algorithm

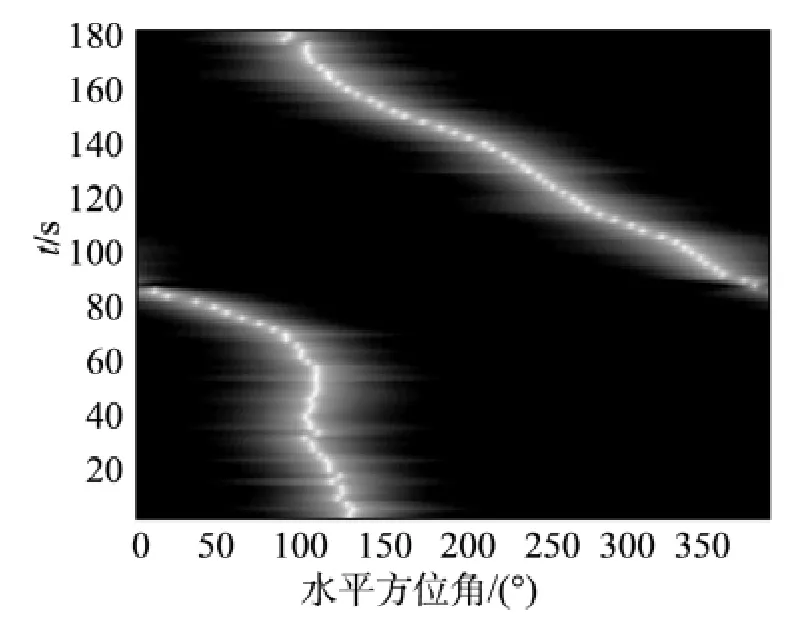
图9 改进MUSIC算法航迹Fig.9 Map of the improved MUSIC algorithm

2种算法都实现了对运动目标的方位追踪，方位角随着时间变化了360°.相比常规算法，改进算法得到的历程图更加清晰，更准确地反映出目标的运行轨迹，湖试数据的处理结果充分地验证了改进算法的有效性.

3 结束语

本文介绍了一种噪声环境下单矢量水听器高分辨方位估计的新方法.该算法将矩阵空域滤波器引入单矢量水听器波束优化设计中，并对常规MUSIC算法方位谱做了相应修改得到改进的定向算法.仿真结果表明，空域滤波器的引入成功优化了单矢量水听器的定向波束，使得低信噪比情况下对目标分辨概率提高，主瓣宽度显著减小.湖试数据的处理结果证明了改进算法的有效性，也说明这种算法有一定工程应用价值.

本文仅对方位角估计做了优化改进，如果将单矢量水听器垂直振速偶极子引入阵列流型，还可以估计俯仰角，矩阵空域滤波器可以对俯仰角的估计性能起到改进作用，这将是下一步进行的工作.

［1］STOICA P，WANG Z S，LI J.Robust capon beam forming［J］.IEEE Signal Processing Lett，2003，10(6):172-175.

［2］杨益新，孙超，马远良.宽带低旁瓣时域波束形成［J］.声学学报，2006，31(4):328-333.YANG Yixin，SUN Chao，MA Yuanliang.Broadband lowsidelobe beam forming in time domain［J］.Acta Acustica，2006 ，31(4):328-333.

［3］梁国龙，张锴，付进.单矢量水听器的高分辨方位估计应用研究［J］.兵工学报，2011，32(8):986-989.LIANG Guolong，ZHANG Kai，FU Jin.Research on highresolution direction-of-arrival estimation based on an acoustic vector-hydrophone［J］.Acta Armamentarii，2011，32(8):986-989.

［4］杨士莪.单矢量传感器多目标分辨的一种方法［J］.哈尔滨工程大学学报，2003，24(6):591-595.YANG Shie.Method of multi-sources distinguishing by single vector transducer［J］.Journal of Harbin Engineering U-niversity，2003，24(6):591-595.

［5］WONG K T.Beam patterns of an underwater acoustic vector hydrophone located away from any reflecting boundary［J］.IEEE Jof Oceanic Engineering，2002，27(3):628-637.

［6］黄玉林，梁国龙，刘凯，等.基于FRFT的单矢量水听器目标方位估计［J］.应用科技，2011，38(2):9-12.HUANG Yulin，LIANG Guolong，LIU Kai，et al.Application of FRFT to DOA estimation based on a single vector hydrophone［J］.Applied Science and Technology，2011，38(2):9-12.

［7］张揽月，杨德森.基于MUSIC算法的矢量水听器阵源方位估计［J］.哈尔滨工程大学学报，2004，25(1):30-33.ZHANG Lanyue，YANG Desen.DOA estimation based on MUSIC algorithm using an array of vector hydrophones［J］.Journal of Harbin Engineering University，2004，25(1):30-33.

［8］鄢社锋，侯朝焕，马晓川.矩阵空域预滤波目标方位估计［J］.声学学报，2007，32(2):151-157.YAN Shefeng，HOU Chaohuan，MA Xiaochuan.Matrix spatial prefiltering approach for direction of arrival estimation［J］.Acta Acustica，2007 ，32(2):151-157.

［9］鄢社锋，马远良.传感器阵列波束优化设计及应用［M］.北京:科学出版社，2009:231-251.