高噪声环境下的基音频率检测方法研究

刘何来，张正炳，杨顺辽 (长江大学电子信息学院，湖北 荆州 434023)

高噪声环境下的基音频率检测方法研究

刘何来，张正炳，杨顺辽 (长江大学电子信息学院，湖北 荆州 434023)

声道特性及噪声给基音检测带来了严重的影响，针对这一问题，将线性预测残差信号作为去除声道影响的激励信号的近似，再结合自相关函数法检测基音频率的高抗噪性，探讨了用线性预测残差信号的低通自相关函数法检测基音频率。用理论模型验证了该方法的可行性，并就实际信号处理情况和倒谱法及自相关函数法进行了比较。结果表明，该方法有效的减少了声道特性的影响，在高噪声环境下比倒谱法和自相关函数法有更好的性能。

基音检测；线性预测残差；自相关函数；语音

目前基音检测方法[1]主要有时域的平均幅度差法[2]和自相关法[3-4]、频域的倒谱法[5]、时频结合的小波变换分析法[6]以及在此基础上的衍生算法[7-8]。这些方法理论上可有效的检测出基音频率，但噪声环境下，检测性能有不同程度下降。

实际语音信号含有各种背景噪声，考虑到自相关函数法适用于噪声环境下的基音检测，但易受声道特性(共振峰)的影响产生倍频现象，而线性预测残差信号去除了声道影响，可近似看作激励信号。为提高在噪声环境下的基音检测精度，笔者探讨将线性预测残差信号进行低通自相关运算来检测基音频率，并把所得结果和自相关法及倒谱法进行比较。

1 语音信号产生模型

图1 语音信号产生模型

语音是由气流激励声道，最后从嘴唇或鼻孔，或同时从嘴唇和鼻孔辐射出来而形成的。基于声道的语音产生模型就是从这一角度描述语音的产生过程，如图1所示[9]。图1所示语音产生模型表明，浊音可以看作是一个周期信号激励于系统的响应，清音则是随机噪声激励于系统的响应。显然，浊音中的基音受到了声门模型、声道模型和辐射模型的综合影响，正是这些模型影响着基音检测的准确性。

基音频率一般处于80～500Hz之间，低通滤波能不同程度上滤除第2和第3共振峰的影响，对第1共振峰无法消除，而声道特性中的第1共振峰频率与基音频率最为接近，其对基音检测影响最大。

2 原理分析

2.1线性预测分析

在随机信号谱分析中，常把一个时间序列模型化为白噪声序列作用于一个数字滤波器后产生的输出。线性预测分析的基本原理是将被分析的信号看作是白噪声序列激励某个模型的输出，这样就可以用模型参数来描述信号。通常所设定的模型为“全极点模型”或“AR模型”，即模型中只包含有限极点而没有零点。而语音是声道冲激响应和声门激励的卷积，如不考虑鼻音和摩擦音，语音的声道系统函数就是一个全极点模型，因此，可用线性预测分析的方法求声道系统函数[10]。

按照上述思路，将图1的语音信号产生模型中的声道模型、脉冲模型及辐射模型用一个时变的数字滤波器来等效，其系统函数为：

(1)

式中，G为增益；a1,a2,…,ap称为线性预测系数；p为线性预测器阶数。

因此，语音信号s(n)和激励信号u(n)之间的关系可表示为：

(2)

(3)

线性预测残差用e(n)表示为：

(4)

比较式(2)和式(4)可知e(n)=Gu(n)，即预测残差信号可看作原始激励信号的加权。

按最小均方误差准则可得到唯一的一组线性预测系数，使e(n)逼近激励信号。原始信号与预测语音信号越接近，e(n)就越接近原始激励信号。理论上残差信号e(n)中不包含声道响应信息，主要反映了原始激励信息，用e(n)去进行基音检测，将较大程度地提高基音检测的准确度。线性预测残差信号中通常含有很多高频成分，可先对预测残差信号进行低通再用于检测基音。为保证预测的准确性，使残差信号更接近于激励信号，实验采用Burg法求线性预测系数[11]。

2.2自相关函数法

对于能量有限的语音信号来说，采用短时分析方法，可以定义短时自相关函数为：

式中，w(n)是偶对称的窗函数；k是移位距离。

自相关函数在基音周期的整数倍点上取得峰值，可根据自相关最大值的位置来估算浊音信号的周期，通常取第1峰值点为基音周期。自相关函数法特别适用于噪声环境下的基音提取。通常基音频率与第1共振峰频率比较接近，单独使用自相关函数法常会产生半频或倍频现象。结合线性预测残差和自相关函数，对预测残差求短时自相关，可有效克服声道共振峰的影响，并且能适应噪声的影响。

3 试验结果与分析

3.1理论模型验证

通过对理论模型的处理来验证笔者提出方法的可行性。声门和声道作用的综合影响模拟[12]如下：

而发浊音时的激励信号为：

x(n)=δ(n)+αδ(n-N0)+α2δ(n-2N0)+…

式中，h(n)为声道模型的冲激响应；δ(n)为单位冲激函数。

图2 理论模型及处理结果

令β0=0.98,β1=1,α=0.9,r=0.99,θ=π/6,N0=15，这时声道模型如图2(a)所示，激励信号的波形如图2(b)所示，图2(c)为声道和激励信号的卷积，即声音的模拟。图2(d)是将图2(c)中的信号经线性预测得到信号的线性预测残差信号。可见，线性预测残差信号基本与原激励信号相同，周期性保存完好，幅度对应成比例，而且受声门和声道特性影响较小。这表明用线性预测残差信号近似浊音激励信号可减少声门和声道特性的影响，提高基音检测的精度。

3.2实际信号的处理

下面用试验来验证线性预测残差的低通自相关函数法进行基音检测的有效性。实验所用语音样本为在安静的室内采集的男声浊音“啊”的一段语音信号，采样率为8KHz，16bit量化,对语音信号进行分帧处理，每帧40ms，帧移20ms。

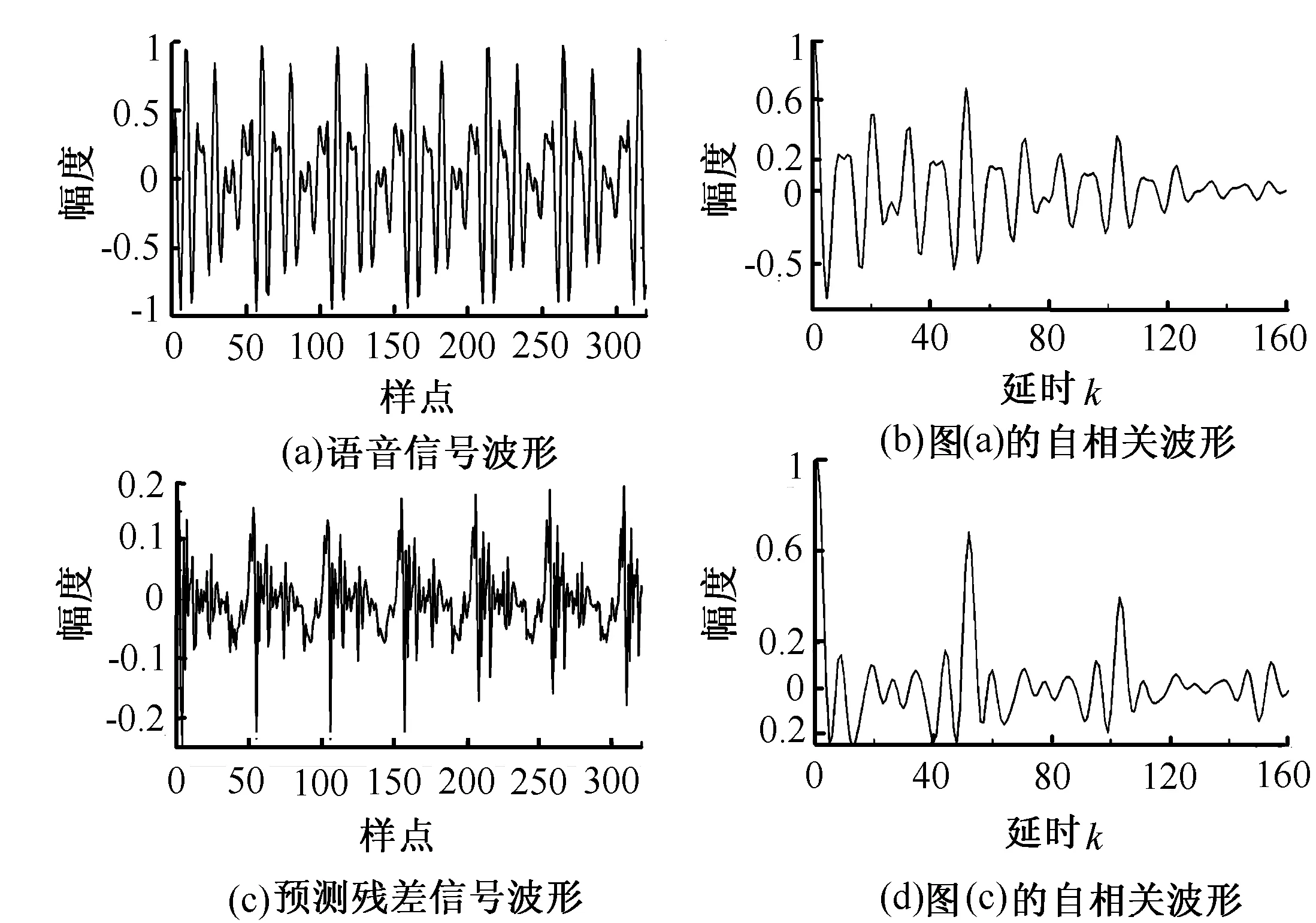
图3 语音信号及预测残差的时域波形及各自自相关波形

图3(a)为一帧语音信号，从图上可以估算出基音周期为51样点，其基因频率为8000/51=156.86Hz，图3(b)为图3(a)的自相关波形。图3(c)为线性预测残差信号的波形，可以看出有很多类似于噪声干扰的高频成分的存在，为提高基音检测的准确性，图3(d)为图3(c)的低通自相关波形。比较图3(b)和图3(d)可以看出，从2幅图上均能有效的检测出基音周期，但图3(d)的自相关波形在非周期对应位置起伏相对较小，即受声道特性的影响较小。

图4是在高信噪比(10dB)时分别采用低通自相关法、倒谱法和线性预测残差的低通自相关法对所采集的一段语音样本进行连续30帧基音检测结果对比，3种检测方法均能有效的检测出基音频率，检测结果和时域估测一致，其中纵坐标为语音的基因频率，横坐标为语音段帧序号。

图5为对低信噪比(-3dB)下语音样本采用上述3种方法进行基音检测结果，自相关法由于受声道特性的影响，检测结果中出现倍频现象，波形起伏严重；倒谱法受噪声影响基音检测结果波动较大；线性预测残差的低通自相关法基音检测结果整体较为平滑，一定程度上克服了倍频现象，抗噪性能优良。

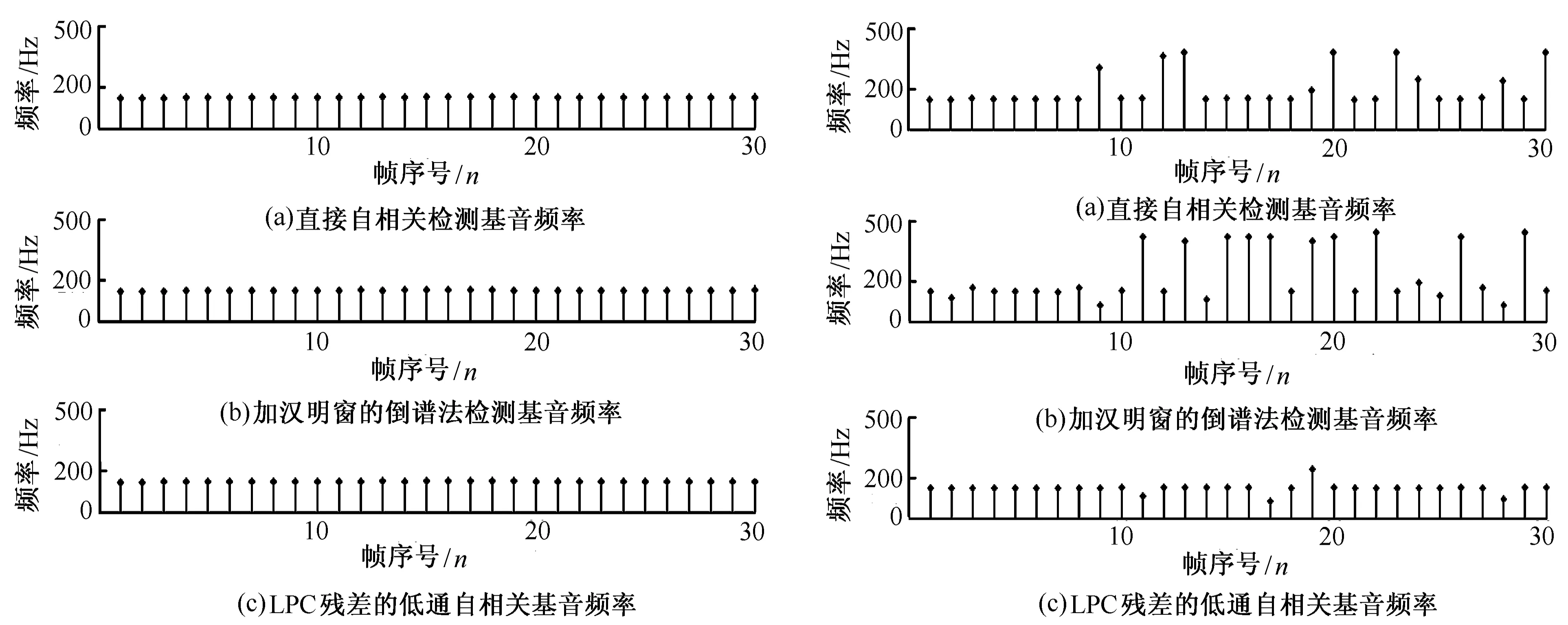
图4 高信噪比下3种方法检测基音频率对比 图5 低信噪比下3种方法检测基音频率对比

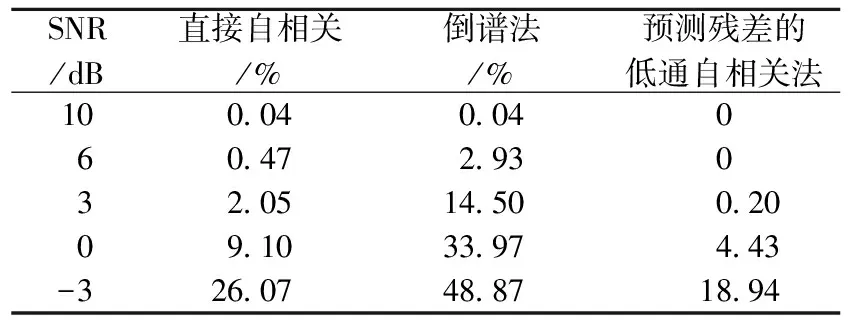
表1 不同信噪比时误检率对比

表1是对语音样本在不同信噪比下通过大量试验得出的基音误检率对比结果。随着信噪比的下降，3种方法的误检率都会上升，倒谱法的性能下降最为剧烈，高噪声情况下，线性预测残差自相关法误检率要小于另2种方法。

[1]冯康, 时慧琨. 语音信号基音检测的现状及展望[J]. 微机发展, 2004, 14(3): 95-98.

[2]王恩成, 苏腾芳, 袁开国, 等. 基于线性预测编码与AMDF的高精度基音检测算法[J]. 计算机应用, 2012, 32(4): 1180-1183.

[3]Shimamura T,Kobayashi H.Weighted autocoorelation for picth extraction of noisy speech[J]. IEEE Trans on Speech Audio Processing, 2001, 9(7): 727-730.

[4]Zhao Qi-fang,Shimamura T, Suzuki J.A Robust Algorithm for Formant Frequency Extraction of Noisy Speech[J].ISCAS,1998,5:534-537.

[5]金学成, 汪增福. 基于线性预测残差倒谱的基音周期检测[J]. 模式识别与人工智能, 2008, 21(1): 104-110.

[6]Kadambe S, Boudreaux-Bartels G F.Application on the wavelet transform for pitch detection of speech signals[J].IEEE Trans on Inform, Theory, 1992, 38(2): 917-924.

[7]李晋，江成，刘甫.改进的基音检测算法[J].计算机工程与应用，2011，47(3)：117-119.

[8]郑继明，王劲松. 语音基音周期检测方法[J].计算机工程，2010,36(10)：273-275.

[9]胡航. 语音信号处理(第4版)[M]. 哈尔滨: 哈尔滨工业大学出版社, 2009.7.

[10]徐金甫，陈小利.基于线性预测的综合基音检测法[J].计算机工程与设计，2008,29(4):891-893.

[11]赵晓群. 数字语音编码[M]. 北京: 机械工业出版社, 2007.

[12]杨顺辽, 李永全. 数字信号处理实现与实验[M]. 武汉: 华中科技大学出版社, 2011.

2012-10-26

刘何来(1985-)，男，硕士生，现主要从事图像、语音信号处理方面的研究工作。

TN912.3

A

1673-1409(2013)01-0046-04

[编辑] 洪云飞