基于自适应最优消零的无线传感器网络数据压缩算法研究
蒋鹏,吴建峰,,吴斌,董林玺,王达
(1.杭州电子科技大学 信息与控制研究所,浙江 杭州 310018;2.杭州电子科技大学 射频电路与系统教育部重点实验室,浙江 杭州 310018;3.杭州市质量技术监督检测院,浙江 杭州 310018)
1 引言
在无线传感器网络(WSN, wireless sensor network)中,传感器节点所采集的原始数据存在着大量的冗余信息,包括同一节点在相邻时刻所采集数据在时间上的冗余以及地理区域上邻近节点所采集数据在空间上的冗余,如果传送携带了大量冗余信息的数据,将浪费通信带宽、增加网络延时和节点能耗,进而会影响整个传感器网络系统的稳定性和寿命,传输原始数据前对冗余信息进行压缩是一种能有效降低节点能耗的机制[1]。
近年来,研究人员提出了许多面向无线传感器网络的数据压缩算法。基于时间相关性的数据压缩算法是一类典型的压缩算法,它常常借助一些经典编码技术,如Huffman[2]、LZW[3]、RLE[4]等,侧重于挖掘数据时间相关性,去除数据的时间冗余。基于空间相关性的数据压缩算法也是一类典型的压缩算法,它往往与分簇机制相结合[5~7],力求充分挖掘数据空间相关性,降低并平衡网络各节点的能耗。近年来,基于时间和空间相关性的数据压缩算法受到越来越多的关注,如Ciancio和Donoho等人提出的算法[8,9]不但涉及去除数据的时间冗余,还探讨了如何建立一条最优的路径,使得数据在沿着这条路径传递时能够最大限度地去除空间冗余。
在无线传感器网络中,差分机制(difference mechanism)常常被应用在数据压缩中[10~12]。结合差分机制的数据压缩算法相同之处在于通过选择一个参考数据,单个传感器节点只需要传送原始感知数据与参考数据之间的差值,从而去除时间冗余,或者地理区域上相邻的传感器节点只需要传输各自原始感知数据与参考数据之间的差值,从而去除空间冗余,而不同之处在于对差值编码的选择。一种较为简单的差分编码压缩算法(DCCM, differential code compression method)是对差值进行二进制编码[12],然而DCCM算法存在以下不足之处。
1) DCCM 算法没有充分考虑参考数据与感知数据序列相关性之间的关系,往往只是简单地将感知数据序列的平均值作为参考数据,缺乏合理性。
2) DCCM 算法只是简单地对感知数据序列和参考数据进行一次性求差并对差值进行二进制编码,无法充分有效地挖掘数据相关性。
受到 DCCM 算法的启发,本文提出了一种新的基于自适应最优消零的传感器网络数据压缩(AOZS)算法,AOZS算法首先对递增排列的感知数据序列进行相关位和位数因子分析,以寻找一个最优位数因子,然后利用该最优位数因子对数据序列进行消零运算和二进制编码。AOZS算法属于无损压缩算法,能够对传感器网络的数据进行有效地压缩,减少网络中传输的数据量,降低节点能耗,减小网络延时。
2 自适应最优消零压缩方法
下面给出自适应最优消零压缩算法所涉及的相关术语。
相关位corr,表示数据序列中相等的数据。在递增排列的数据序列(Z1,Z2,…,Zn)中,若 Zk(1<k≤n)的相关位为1,则Zk与Zk−1相等,若相关位为0,则Zk与Zk−1不相等,其中,Z1的相关位始终为0。
编码因子 d,指每阶消零运算中数据序列所减去的整数值,算法将根据可选位数因子对其进行二进制编码。
最大编码因子Di,指位数因子Ci可以表示的最大数值,Di反映了相邻数据间可允许的最大差值,如果相邻数据变化过大,则可以相应地增大位数因子,以扩大编码的适用范围。
位数因子Ci,指用来对编码因子进行二进制编码的位数。
本文采用3位二进制来表示位数因子,000~111分别表示用2~9位二进制对编码因子d进行编码,称之为C2~C9编码,Ci(i=2,3,…,9)相应的最大编码因子为Di(i=2,3,…,9)。位数因子Ci,Ci编码和最大编码因子Di之间的关系如表1所示。

表1 Ci、Ci编码和Di之间的关系
自适应最优消零压缩算法的原理如图1所示。

图1 自适应最优消零压缩算法的原理
自适应最优消零压缩算法原理:给定一组递增排列的整数数据序列(Z1,Z2,…,Zn),首先对其进行相关位和位数因子分析,求出所有可选的位数因子Cx,并计算相应的编码长度 Qx,将最短编码长度Qmin对应的位数因子作为该数据序列的最优位数因子Coptimal,然后基于该最优位数因子执行消零运算和编码,即在每阶消零运算下将数据序列中的非零数据减去一个编码因子d,使得数据序列从小到大依次被消为零,最后,对该数据序列的相关位corr、最优位数因子Coptimal以及编码因子d进行二进制编码。
下面详细阐述可选的位数因子 Cx,编码长度Qx,最优位数因子Coptimal,最短编码长度Qmin以及编码因子d的计算原理。
位数因子Ci(i=2,3,…,9)的选择会影响数据最终的编码长度,若选择过小,则很难恢复原始数据,若选择过大,则导致最终编码过长。设有M个递增排列的整数数据(Z1,Z2,…,ZM),其中,有N个数据是互不相等的,最小值为α,相邻数据间最大差值为β。设 Cx为消零编码运算的可选位数因子,则Cx满足以下条件

若Tα=0或Tβ=0,则表明数据大小或变化幅值超出了位数因子Ci所能编码的范围,此时需要用3位以上的二进制来表示位数因子Ci,以扩大编码的适用范围。
设可选位数因子Cx的最大编码因子为Dx,则数据序列最终的编码长度Qx为

给定一组递增排列的整数数据序列,最优位数因子为Coptimal,Coptimal的最大编码因子为Doptimal,且在第 i(i=1,2,…)阶消零运算时数据序列中最小非零数据为Zmin,则第i阶消零运算的编码因子d为

例如,有一组递增排列的整数数据序列{15,18,18, 24,26,26},容易得到corr=001001,M=6,N=4,α=15,β=6,由式(2)、式(3)可得Tα=4,Tβ=3,因此可选位数因子Cx∈[3,4]。由式(4)得到Qx|(Cx=3)=27,Qx|(Cx=4)=25,因此最优位数因子Coptimal=C4,接着执行消零运算,第一阶消零运算中,由式(5)得到编码因子 d=15,原始数据序列减去编码因子15后,得到一阶数据序列{0,3,3,9,11,11};第二阶消零运算中,由式(5)得到编码因子d=3,一阶数据序列中非零数据减去编码因子3后,得到二阶数据序列{0,0,0,6,8,8};如此反复运算直到数据序列中各数据均被消为零,最后,对相关位corr和最优位数因子C4进行编码,此外,因为C4=4,所以采用4位二进制对各阶编码因子{15,3,6,2}进行编码,C4编码的压缩流程如表2所示。

表2 C4编码压缩流程
由表 2可得,编码为 100, 001001, 11110011,0110, 0010。其中,编码的1~3bit是最优位数因子C4的二进制编码,4~9bit是相关位 corr编码,10~25bit是编码因子d的4位二进制编码。
通常,传感器节点所采集的为非整数数据,因此需要对上述自适应最优消零压缩算法做相应改进。给定一组递增排列的数据序列,数据的最小精度为 k(k<1),最小数据为 Zmin,相邻数据间最大差值为λ,引入一个消整因子η,minZη=,其中,为向下取整符号,设

本文采用8位二进制对消整因子η进行编码,则数据序列最终编码长度Qx的计算公式为

例如,有一组递增排列的数据序列{21.7,21.8,22.4,22.4,22.5,23.0},容易得到corr=000100,M=6,N=5,Zmin=21.7,k=0.1,λ=0.6,η=21,由式(6)、式(7)可以得到α=7,β=6,由式(2)、式(3)可得Tα=Tβ=3,可选位数因子 Cx=C3,由式(8)得到Qx|(Cx=3)=32,因此最优位数因子 Coptimal=C3。首先,将原始数据序列减去消整因子η,得到数据序列{0.7,0.8,1.4,1.4,1.5,2.0},再乘以最小精度的倒数1/ k,得到数据序列{7,8,14,14,15,20},然后执行消零运算,第一阶消零运算中,由式(5)得到编码因子 d=7,数据序列减去编码因子7后,得到一阶数据序列{0,1,7,7,8,13};第二阶消零运算中,由式(5)得到编码因子 d=1,一阶数据序列中非零数据减去编码因子1后,得到二阶数据序列{0,0,6,6,7,12};如此反复运算直到数据序列中各数据均被消为零,最后,对消整因子η、相关位corr和最优位数因子 C3进行编码,此外,因为C3=3,所以采用 3位二进制对各阶编码因子{7,1,6,1,5}进行编码,C3编码的压缩流程如表 3所示。
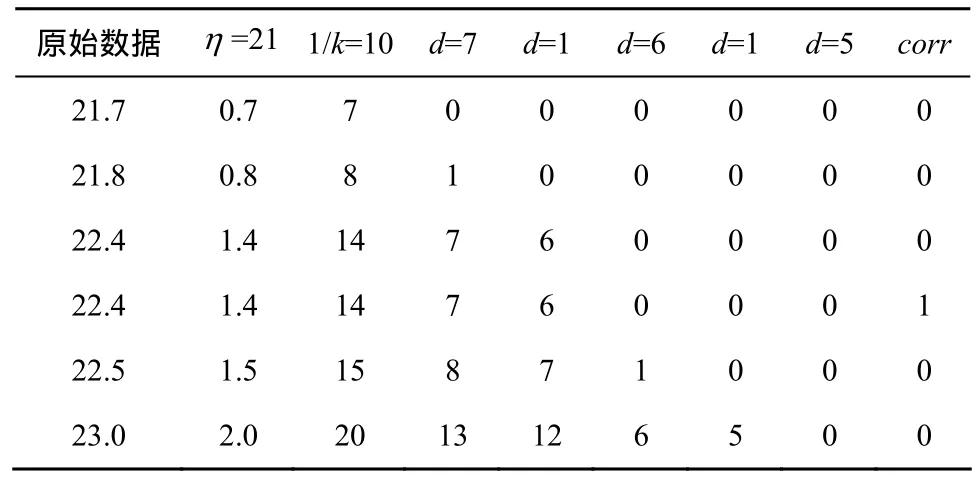
表3 C3编码压缩流程
由表3可得,编码为00010101, 011, 000100, 111,001, 110, 001, 101。其中,编码的1~8bit是消整因子η的二进制编码,9~11bit是最优位数因子 C3的二进制编码,12~17bit是相关位corr编码,18~32bit是编码因子d的3位二进制编码。
3 算法描述
大规模的传感器网络通常被划分为多个簇,簇内各传感器节点将采集数据发送到簇头节点,簇头节点将数据发送给上一层节点,层层递进,直到基站为止,从而形成一个树形分簇结构,在这种树形分簇结构下,基于AOZS的传感器网络数据压缩算法流程描述如下。
1) 簇内传感器节点将在时刻{t1,t2,…,tn}采集到的n个数据{d1,d2,…,dn}进行递增排序,同时也对采集时刻进行相应排序,根据自适应最优消零压缩算法原理计算数据序列的最小编码长度 Qmin_d,并求出相应的最优位数因子 Coptimal_d,然后基于最优位数因子对数据序列进行消零运算和编码,去除时间冗余,得到压缩后的数据。
2) 传感器节点将压缩后的数据传送到簇头节点,数据分组格式为{node_id, <time_stamp>,data_ code},其中,node_id为传感器节点的ID号,<time_ stamp>为递增排列后各数据所对应的时间槽,data_code为数据序列的编码,前8位表示消整因子。
3) 簇头节点接收簇内各传感器节点发送的数据分组后,分别提取 data_code中消整因子η的二进制编码并转换为十进制数,得到消整因子序列,然后对消整因子序列进行递增排序,同时也根据消整因子序列的顺序对各节点的数据分组进行相应排序,并根据自适应最优消零压缩算法原理计算其最小编码长度Qmin_s,求出相应的最优位数因子Coptimal_s,然后基于最优位数因子对消整因子序列进行消零运算和编码,去除空间冗余,得到再压缩后的数据。
4) 簇头节点将再压缩后的数据发送到上一层节点,数据分组格式为{s_code, <cluster_code>},其中,s_code为消整因子序列的编码,<cluster_ code>为递增排列后的消整因子序列所对应的传感器节点数据分组{node_id, <time_stamp>, data_ code},但此时data_code中的消整因子编码已被提取。
5) 上一层节点直接将已经去除了时间和空间冗余的数据分组{s_code, <cluster_code>}路由至基站。
基于AOZS的传感器网络数据压缩算法流程如图2所示。
4 仿真算例
本节首先介绍了几项传感器网络数据压缩算法的性能评价指标,然后通过 NS2仿真实验对AOZS算法和DCCM算法进行了比较。

图2 基于AOZS的传感器网络数据压缩算法流程
4.1 性能评价指标
1) 压缩比(CR, compression ratio)

其中,SCP为压缩后的数据量,SOR为原始数据量。CR越小,则压缩后的数据量占原始数据量的比例越小,压缩性能越好。
2) 节点平均能耗(AEC, average energy consumption)
采用一阶无线模型(first order radio model)[13]来计算节点能耗

其中,Ep和 Ec分别为节点的计算能耗和无线通信能耗,无线通信能耗Ec可以分为无线发射能耗ETx和无线接收能耗 ERx,由于传感器节点的计算能耗相对于无线通信能耗而言可以忽略不计,因而有

节点的能耗与节点发送或者接收数据分组的时间有关,数据分组越长则节点发送或者接收的时间越长能耗也越大,所以节点的发送能耗ETx可由节点发射功率PTx与数据发送所用时间TTx的乘积表示,节点的接收能耗ERx可由节点接收功率PRx与数据接收所用时间TRx的乘积表示,即


所以节点能耗为

本文对无线发射能耗 ETx和无线接收能耗 ERx的计算建立在基于ZigBee协议的CC2430硬件平台上。CC2430微控器的内核运行在32MHz,无线发射电流为 25mA,无线接收电流为 27mA,供电电压为3.3V,因此无线发射功率PTx=0.0825W,无线接收功率PRx=0.0891W。本文将根据式(14)计算传感器节点的能耗,并将节点的平均能耗作为压缩算法的性能评价指标。
3) 网络延时(ND, network delay)
本文对网络延时的计算建立在基于 ZigBee协议的CC2430硬件平台上,CC2430一个指令周期为1/32μs,网络延时(DNTD)由2部分组成:从采集节点发送数据到接收节点收到数据的传输延时(DTTD),节点运行数据压缩算法产生的计算延时(DCTD),即

4.2 仿真结果与分析
本文所采用的仿真工具为ns-allinone-2.34,数据计算处理工具为 GNU Awk-3.1.5,作图工具为gnuplot-4.3。仿真中节点的属性设置如下:所有节点均为静止状态,节点的无线传播模型为双径地面(two ray ground)反射方式,节点的传输距离为40m,载波侦听范围为 88m,天线采用 Omni Antenna,发射频率为2.4GHz;物理层和MAC层协议采用IEEE 802.15.4,路由层协议采用AODV,流量发生器采用CBR;节点每秒采集发送一次数据分组,发送速率为40kbit/s。

图3 网络场景
仿真时,网络场景如图3所示,整个传感器网络由101个节点组成,横向与纵向相邻的节点相距75m,对角相邻的节点相距5m。网络中包含1个基站(节点号为0)、3个分簇以及每个分簇内的7个采集节点(簇头节点号和采集节点号如表4所示)。节点采集的每个数据长度均为2byte,实验数据来源于Intel-伯克利大学联合研究实验室利用无线传感器节点采集的温度数据,整个仿真运行1000s。接下来本文将分析和比较当节点数据采集量从 10~100之间变化时AOZS算法和DCCM算法的各项性能指标。

表4 簇头和分簇内采集节点号
由图4可以看到,在节点数据采集量相同的条件下,AOZS算法的压缩比低于DCCM算法,压缩性能更优,这是因为AOZS算法能很好地挖掘了数据间的相关性,基于最优位数因子的编码最大程度地去除了冗余信息,本文采用8位二进制对DCCM算法的均值和差值进行编码,因此DCCM算法的压缩比始终高于0.5。随着节点采集数据量的增加,数据的时间相关性越来越高,AOZS算法的编码因子能够描述越来越多的原始数据,充分挖掘了数据的时间相关性,因此压缩比越来越小,逐渐趋于平稳。

图4 AOZS、DCCM算法压缩比对比
节点能耗是衡量传感器网络数据压缩算法性能的一个关键指标,引入数据压缩算法后加节点的计算能耗,但相对于节点的无线通信能耗而言,计算能耗可忽略不计,因此,仿真中的能耗只需考虑节点的无线通信能耗,可通过NS2自带的能量模型获取,仿真程序运行之前设定节点的初始能量、收发功率、数据收发速率,根据数据分组长度便可计算出每次活动后节点的剩余能量,并将其保存至trace文件,仿真结束后通过GNU Awk-3.1.5工具从 trace文件中提取所有节点的剩余能量信息并累加即可得网络的剩余能量。此外,根据节点的初始能量以及节点总数可算出网络的初始总能量,其与网络的剩余能量的差值即为网络运行过程中总能耗,将总能耗与网络总节点数相除即可得出节点的平均能耗。本仿真中,节点总数为101个,各节点的初始能量为 1J,节点收发功率计算基于CC2430硬件平台,发射功率PTx=0.0825W,无线接收功率PRx=0.0891W。
由图5可以看到,在节点数据采集量相同的条件下,AOZS算法的节点平均能耗明显低于DCCM算法,这是因为AOZS算法能够更好地挖掘数据的相关性,最大程度地去除冗余信息。随着节点采集数据量的增加,2种算法的节点平均能耗均会提升,这是由于节点数据采集量增加时,网络传输的数据量必然增加,从而导致节点能耗上升。

图5 AOZS、DCCM算法节点平均能耗对比
仿真中的延时可通过NS2的trace文件和模拟计算获取,trace文件可记录发送节点发送数据分组的时间与接收节点接收数据分组的时间,仿真结束后通过GNU Awk-3.1.5从trace文件中提取并计算各个数据分组从发送节点传输至接收节点的延时,并记录传输次数,将各次延时累加并除以总传输次数即可得传输延时DTTD。节点的计算延时通过模拟计算获得,算法运行的硬件平台基于CC2430,一条指令执行周期为1/32μs,AOZS算法的指令为200条,DCCM算法的指令为50条[12],通过计算即可得计算延时DCTD。DTTD与DCTD相加即可得网络延时DNTD。
由图6可以看到,2种算法的网络延时均随着节点采集数据量的增加而增加。当节点数据采集量较小时,DCCM算法的延时略小于AOZS算法,因为此时影响网络延时的决定性因素是对数据进行压缩的计算延时,而 DCCM 算法的计算延时要小于AOZS算法。随着节点采集数据量的增加,DCCM算法的延时明显大于AOZS算法,因为此时的决定性因素已不是计算延时,而是数据传输引起的延时,AOZS算法大大降低了网络中需要传输的数据量,从而减小了网络延时。

图6 AOZS、DCCM算法网络延时对比
5 结束语
无线传感器网络采集的数据中存在着大量时间和空间冗余信息,本文针对该问题提出了一种自适应最优消零压缩(AOZS)算法,AOZ算法能够自适应地寻找最优位数因子,对递增排列的原始数据序列进行消零运算和编码,使得其最终编码长度最短,从而达到数据压缩的目的。仿真结果表明,AOZS算法的总体性能比DCCM算法更优,能够有效地去除传感器网络采集数据中存在的冗余信息,减少了网络的数据传输量和延时,降低了节点功耗。
[1]JENNIFER Y, BISWANATH M, DIAK G.Wireless sensor network survey[J].Computer Networks, 2008, 52(12):2292-2330.
[2]CAPO-CHICHI E P, GUYENNET H, FRIEDT J M.K-RLE:a new data compression algorithm for wireless sensor network[A].International Conference on Sensor Technologies and Applications[C].Glyfada, Athens, 2009.502-507.
[3]ZHANG H, FAN X P, LIU S Q, et al.Design and realization of improved LZW algorithm for wireless sensor networks[A].International Conference on Information Science and Technology(ICIST)[C].Changsha, China, 2011.671-675.
[4]MO Y B, QIU Y B, LIU J Z, et al.A data compression algorithm based on adaptive huffman code for wireless sensor networks[A].International Conference on Intelligent Computation Technology and Automation (ICICTA) [C].Nanjing, China, 2011.3-6.
[5]XIE L, CHEN L J, CHEN D X.Clustering-based approximate scheme for data aggregation over sensor networks[J].Journal of Software,2009, 20(4):1023-1037.
[6]HU J, SHEN L F.Novel clustering algorithm for wireless sensor networks[J].Journal on Communications, 2008, 29(7):20-29.
[7]ZHU X R, SHEN L F, TAK-SHING P Y.Hausdorff clustering and minimum energy routing for wireless sensor networks[J].IEEE Transactions on Vehicular Technology, 2009,58(2):990-997.
[8]CIANCIO A, PATTEM S, ORTEGA A, et al.Energy-efficient data representation and routing for wireless sensor networks based on a distributed wavelet compression algorithm[A].The Fifth International Conference on Information Processing in Sensor Networks[C].Palo Alto, CA, USA, 2006.309-316.
[9]DONOHO D L.Message passing algorithms for compressed sensing:I.motivation and construction[A].IEEE Information Theory Workshop 2010[C].Cairo, Egypt, 2010.1289-1306.
[10]MARCELLONI F, VECCHIO M.A simple algorithm for data compression in wireless sensor networks[J].IEEE Communications Letters,2008, 12(6):411-413.
[11]范祥辉,李士宁,杜鹏雷等.WSN中一种自适应无损数据压缩机制[J].计算机测量与控制, 2010, 18(2):463-465.FAN X H, LI S N, DU P L, et al.Simple algorithm for self-adapting lossless data compression in WSN[J].Computer Measurement & Control, 2010, 18(2):463-465.
[12]夏永成,陈黎黎,陈曦.无线传感器网络中的数据压缩研究结合小波提升算法和差分机制[J].计算机工程与应用, 2010, 46(2):109-112.XIA Y C, CHEN L L, CHEN X.Research on data compression in wireless sensor networks-with wavelet lifting algorithm and difference mechanism[J].Computer Engineering and Applications, 2010,46(2):109-112.
[13]WANG A, CHANDRAKSAN A.Energy-efficient DSPs for wireless sensor networks[J].IEEE Signal Processing Magazine, 2002, 19(4):68-78.

